 |
Multiple Regressionsanalysen mit SPSS - Beispiele und Aufgaben im Modul XII-6 Multiple Regressions- und Korrelationsmodelle
1. Beispielsrechnungen mit SPSS
Nachstehend wird am Beispiel der Datei Partizipation_1.sav und der dort enthaltenen, abhängigen metrisch-skalierten Variablen Partizipationsprofil und den unabhängigen, im Folgenden als metrisch behandelten, Variablen Geschlecht, Ausbildung, Status und Partizipationspotential gezeigt, wie mit SPSS multiple Regressions- und Korrelationsanalysen rechnerisch durchgeführt werden und wie die Ergebnisse im Hinblick auf Richtung und Stärke des Zusammenhangs der Variablen zu interpretieren sind.
Die Analysen werden mit dem bereits in der einfachen lineare Analyse eingesetzten Programmpaket "Regression" rechnerisch durchgeführt und ausführlich tabellarisch präsentiert. Die Ergebnisse zu den verschiedenen Modellansätzen werden einander gegenübergestellt und vertieft inhaltlich diskutiert.
a) Die Regressions- und Korrelationsanalyse mit der Prozedur "Regression"
Mit der Prozedur "Regression" kann in SPSS nicht nur eine multiple Regressionsanalyse sondern auch eine multiple Korrelationsanalyse durchgeführt werden. Dazu sind in die Eingabefenster neben der abhängigen Variablen das Set der unabhängigen Variablen einzutragen
Die Prozedur "Regression" aufrufen
Screenshot 12-34: Die multiple Regressions- und Korrelationsanalyse anfordern
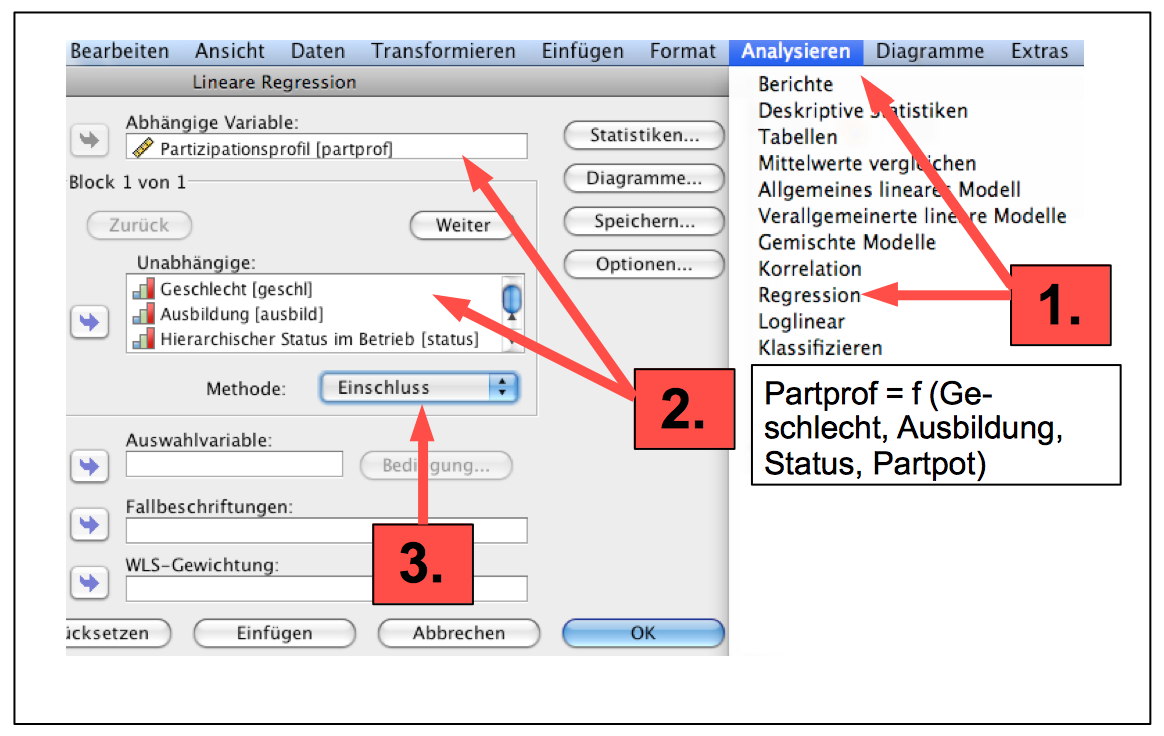
1. "Analysieren > Regression > Linear" aufrufen.
2. Abhängige Variable und Unabhängige eingeben.
3. Methode des Einbezugs der Variablen spezifizieren.
Die mit der Methode Regression verfügbaren Einschlussmethoden
Methode "Einschluss":
Alle erklärenden Variablen bzw. alle Variablen eines Blockes werden auf einmal einbezogen.
Strategisch betrachtet, prüft diese Methode, welche der potentiellen Variablen letztlich in ein Erklärungsmodell eingehen sollten.
Methode "Schrittweise":
Die erklärenden Variablen werden nacheinander nach ihrem jeweils größten Erklärungsbeitrag einbezogen. Bereits aufgenommene Variablen werden wieder entfernt, wenn ihr Erklärungsbeitrag im Verlaufe des Verfahrens von anderen Variablen übernommen wurde.
Diese Strategie erlaubt die schrittweise Verbesserung der Erklärungskraft und die Identifikation der Erklärungsbeiträge der unabhängigen Variablen nach dem statistischen Kriterium des jeweils höchsten Korrelationskoeffizienten.
Methode "Vorwärts":
Diese Methode entspricht der Methode "Schrittweise" bis auf die Entfernung nicht mehr relevanter Variablen.
Methode "Rückwärts":
Alle erklärenden Variablen werden auf einmal einbezogen und bei zu geringem Beitrag wieder eliminiert. Dieser Ansatz stellt die Umkehrung des schrittweisen Einbezugs dar und wird im Folgenden nicht explizit vorgestellt.
Methode "Blockweise":
Die erklärenden Variablen werden nach einer vorab festgelegten Reihenfolge einzeln oder in Gruppen in aufeinander folgenden Eingabeblöcken einbezogen. Die Blöcke werden durch Klicken auf den "Weiter"/("Nächste")-Button von einander getrennt
Diese Strategie ist angebracht, wenn unter den unabhängigen Variablen kausale Abhängigkeiten gegeben sind, die den Modellaufbau steuern sollen.
Methode "Entfernen":
Alle erklärenden Variablen eines Blockes werden eliminiert. Dieser Ansatz erlaubt die Entfernung von Blöcken der Methode Blockweise.
b) Das Analysemodell "Einschluss"
Die Methode "Einschluss" wird entsprechend dem Screenshot 12-34 aufgerufen.
-
Screenshot 12-35: Die Modellzusammenfassung "Einschluss"

Im Vergleich zur einfachen Regression zwischen den Variablen Partizipationsprofil und -potential hat sich R2 im multiplen Modell um 11,9 % verbessert.
-
Screenshot 12-36: Die Anova Tabelle "Einschluss"
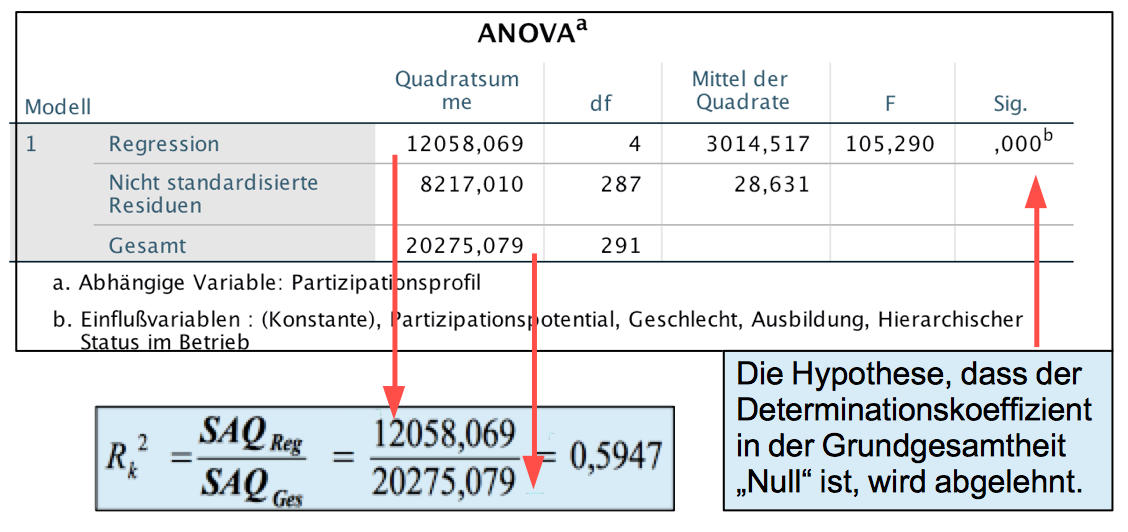
Die ANOVA-Tabelle liefert die Daten zur Berechnung von R2.
-
Screenshot 12-37: Die Tabelle der partiellen Regressionskoeffizienten "Einschluss"
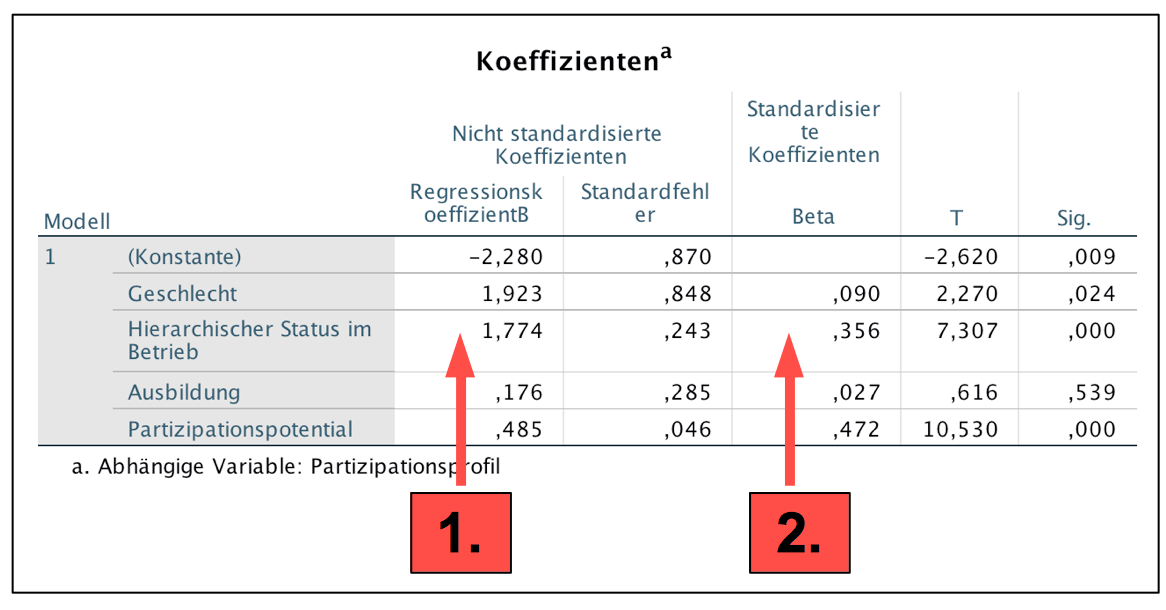
1. Die Interpretation der nicht standardisierten Koeffizienten:
a ist das Ausmaß der realen Beteiligung, wenn alle unabhängigen Variablen = „0“
b1 gibt an, um wie viel die reale Beteiligung zunimmt, wenn das Geschlecht um „1“ steigt (d.h. von weiblich zu männlich wechselt) *)
b2 gibt an, um wie viel die reale Beteiligung zunimmt, wenn die Ausbildung um eine Stufe steigt. *)
b3 gibt an, um wie viel die reale Beteiligung zunimmt, wenn der Status um eine Stufe steigt. *)
b4 gibt an, um wie viel die reale Beteiligung zunimmt, wenn die gewünschte Beteiligung um „1“ steigt. *)
*) = bei Konstanz der anderen unabhängigen Variablen.
2. Die Interpretation der standardisierten Koeffizienten:
beta1 – beta4 geben an, um wie viele Standardabweichungen die reale Beteiligung zunimmt, wenn die Standardabweichung der jeweiligen Variable um „1“ steigt.
Die beta-Werte zeigen die relative Bedeutung des Einflusses der einzelnen unabhängigen Variablen an.
Danach hat die gewünschte Beteiligung den stärksten, der Status den zweitstärksten Einfluss.
Anmerkung: Zur Darstellung und Interpretation der induktiven Aspekte der Regressios- und Korrelationsanalyse vgl. den Verweis am Ende des Abschnitts.
c) Das Analysemodell "Schrittweise"
Die Methode "Schrittweise" wird aufgerufen, wie in Screenshot 12-38 demonstriert.
Screenshot 12-38: Aufruf der Methode "Schrittweise"
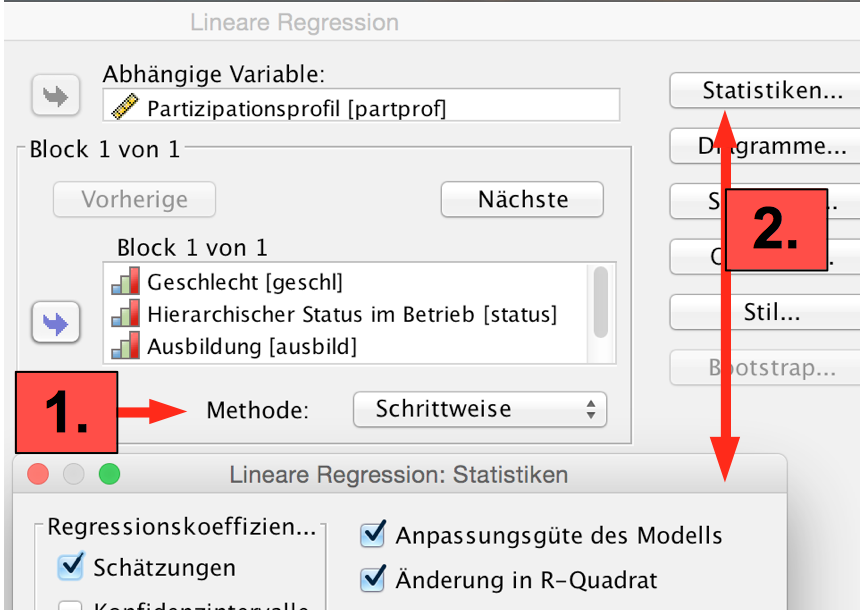
1. Methode "Schrittweise" wählen.
2. Über "Statistiken" die markierten Ergebnisse anfordern.
-
Screenshot 12-39: Die Modellzusammenfassung "Schrittweise"
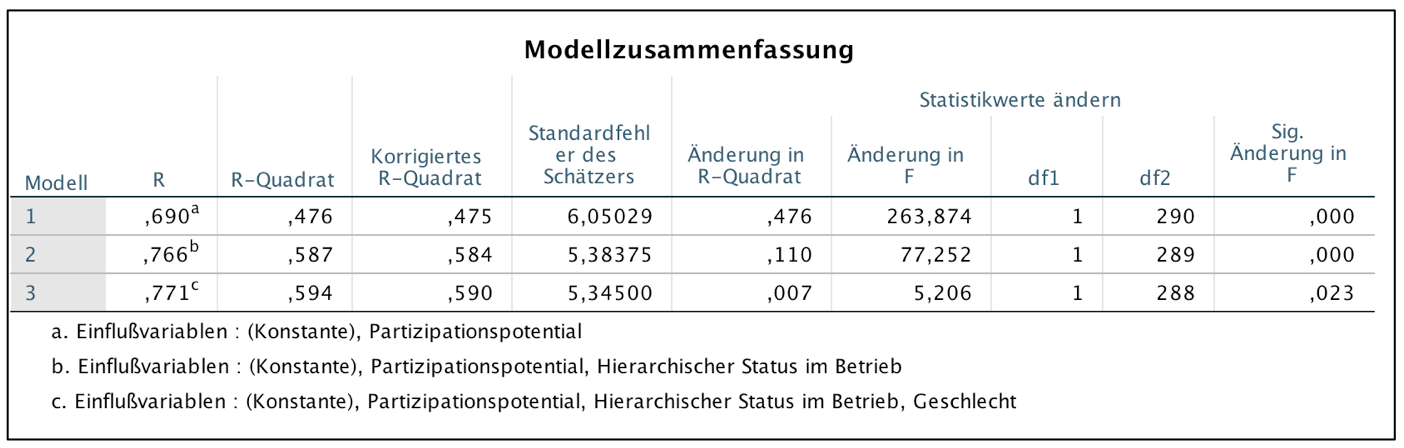
Die Modellzusammenfassung zeigt:
Die Variablen werden in der Reihenfolge: gewünschte Beteiligung, Status, Geschlecht aufgenommen.
Die Variable Ausbildung wird nicht aufgenommen (vgl. dazu den Kommentar zum Screenshot 12-41).
Mit jeder zusätzlichen Variablen steigt R-Quadrat.
Dabei nehmen die Änderungen in R-Quadrat kontinuierlich ab.
Der Determinationskoeffizient des schrittweisen Modells liegt mit einem Betrag von 0,594 geringfügig unter dem Wert für das Einschluss-Modell von 0,595.
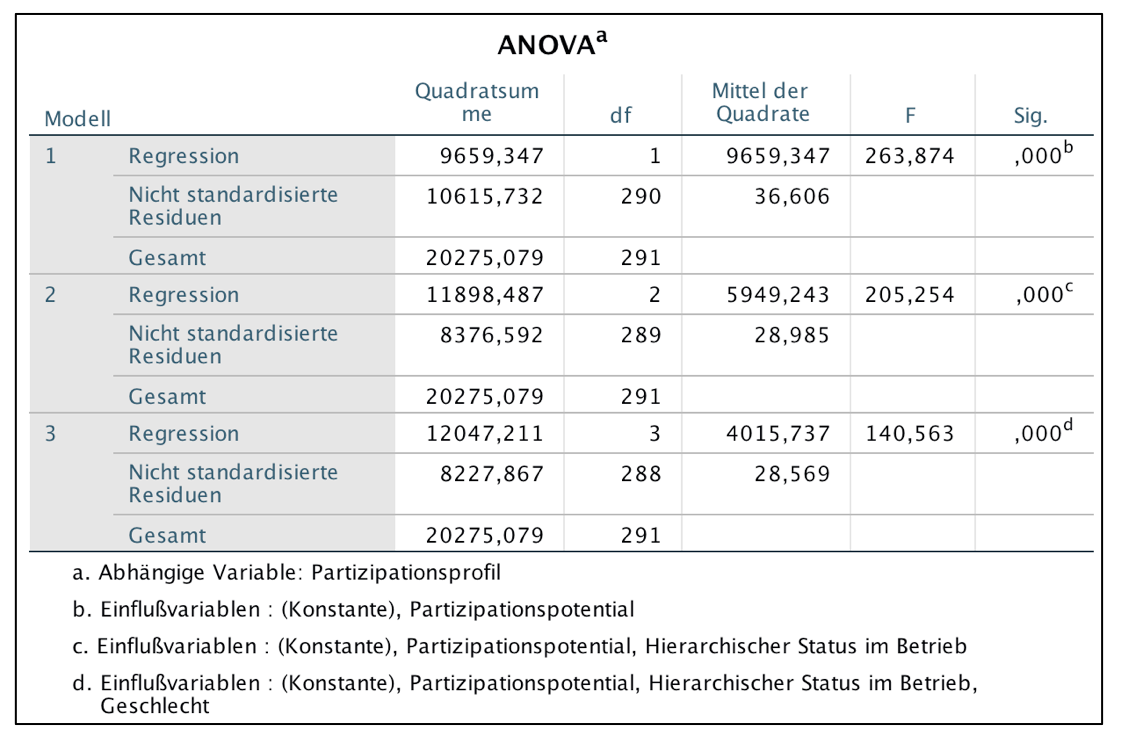
Screenshot 12-40: Die Anova Tabelle "Schrittweise"
Screenshot 12-41: Die Tabelle der partiellen Regressionskoeffizienten "Schrittweise"
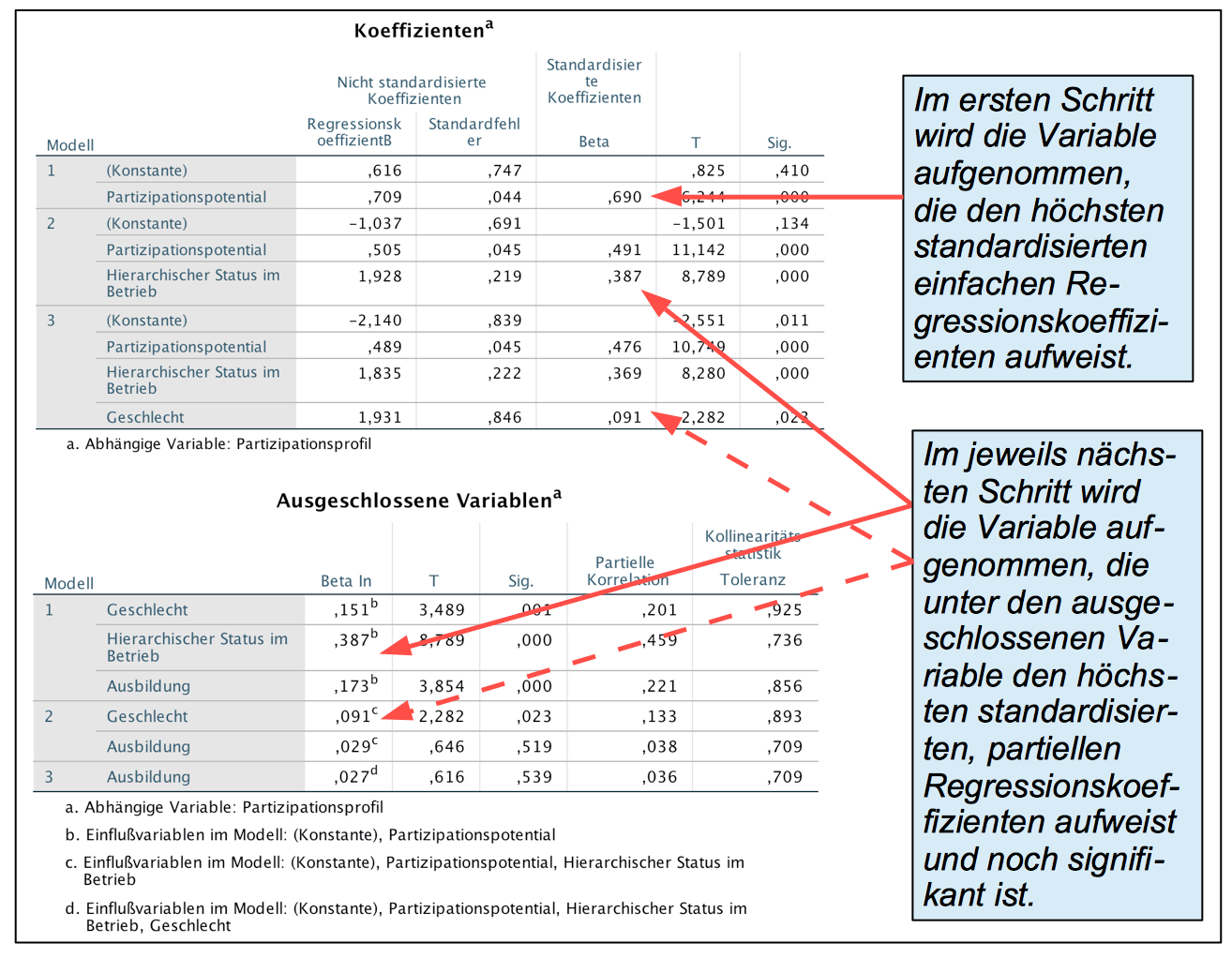
Bemerkungen zu den standardisierten/nicht-standardisierten Koeffizienten:
Von den im Modell 1 noch ausgeschlossenen Variablen Geschlecht, Ausbildung und Status liegt der Erklärungsbeitrag der Variablen Ausbildung über dem der Variablen Geschlecht, aber unter dem der Variablen Status, die deshalb in das Modell 2 aufgenommen wird.
Im Modell 2 ist nun der Beitrag der Variablen Ausbildung deutlich unter den der Variablen Geschlecht gesunken, da ihre gemeinsame partielle Varianz mit der Variablen Status ihr nicht mehr zugerechnet wird. Sie scheidet deshalb aus der Analyse aus.
Zu beachten ist auch die Veränderung der nicht standardisierten Koeffizienten von Modell zu Modell.
Im schrittweisen Modell 3 unterscheiden sich die Werte der partiellen Koeffizienten kaum noch von den Werten des Einschluss-Modells.
Anmerkung: Zur Darstellung und Interpretation der induktiven Aspekte der Regressios- und Korrelationsanalyse vgl. den Verweis am Ende des Abschnitts.
d) Das "hierarchische" Analysemodell
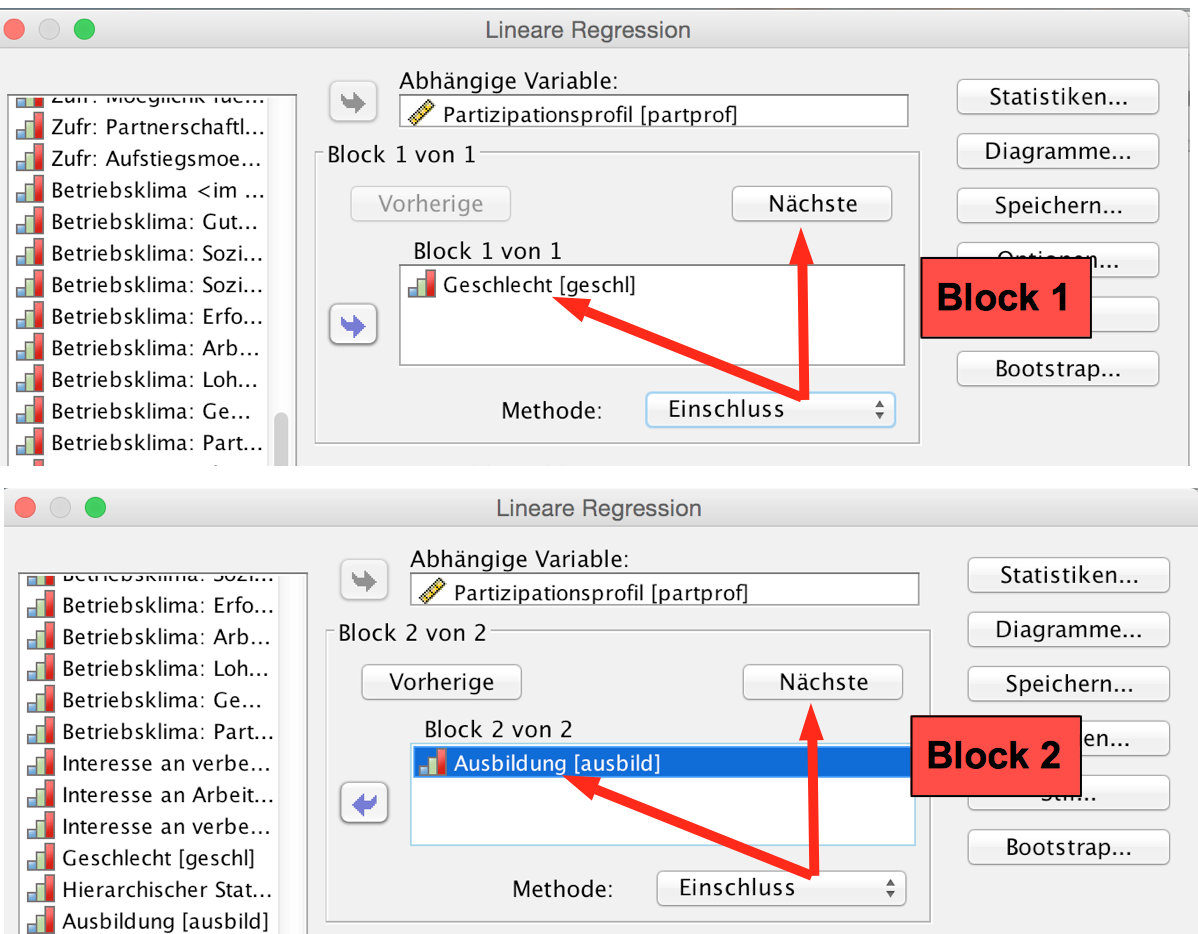
Die hierarchische Methode wird entsprechend den Screenshot 12-42 und 43 aufgerufen.
|
Screenshot 12-42: Block 1 und 2 anfordern
|
| Screenshot 12-43: Block 3 und 4 anfordern
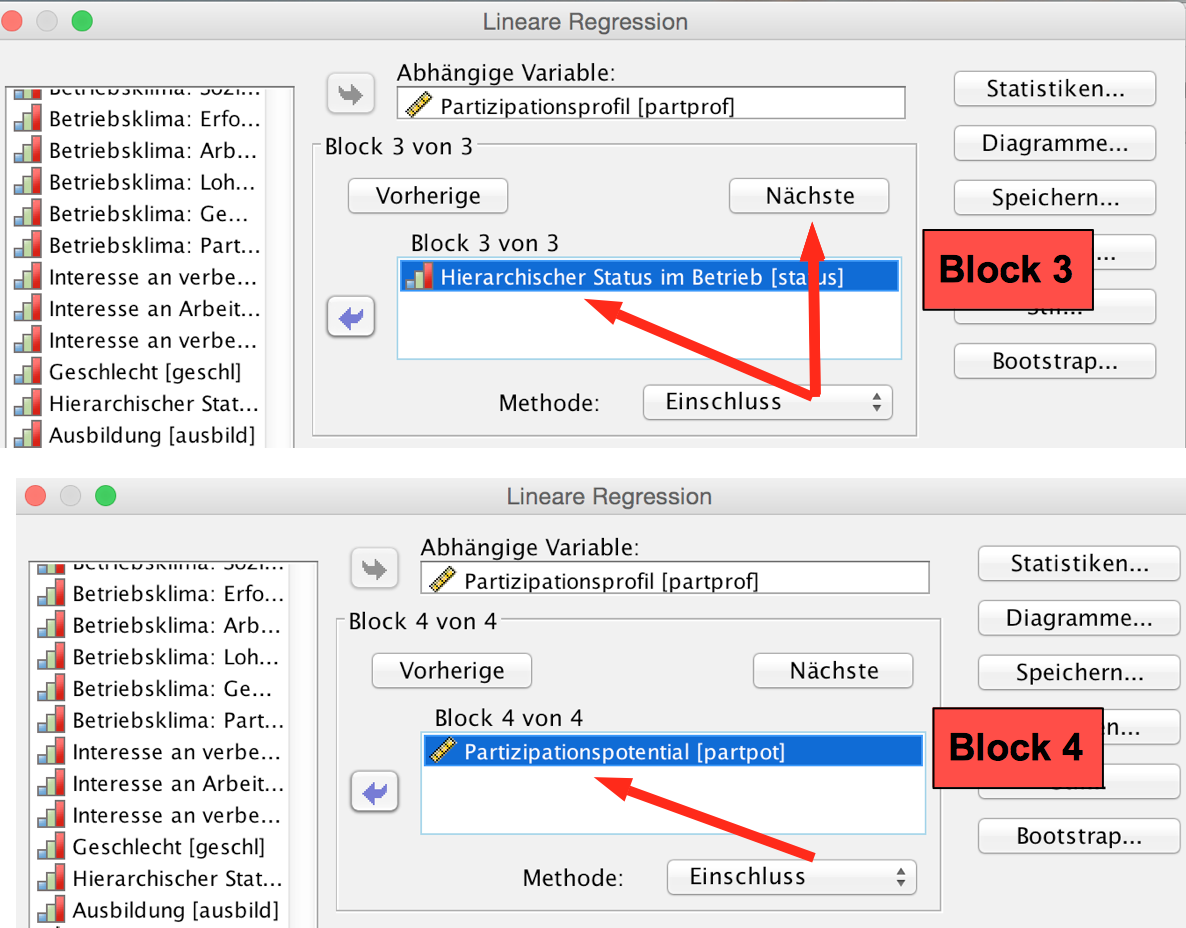
|
-
Screenshot 12-44: Die Modellzusammenfassung "hierarchisch"
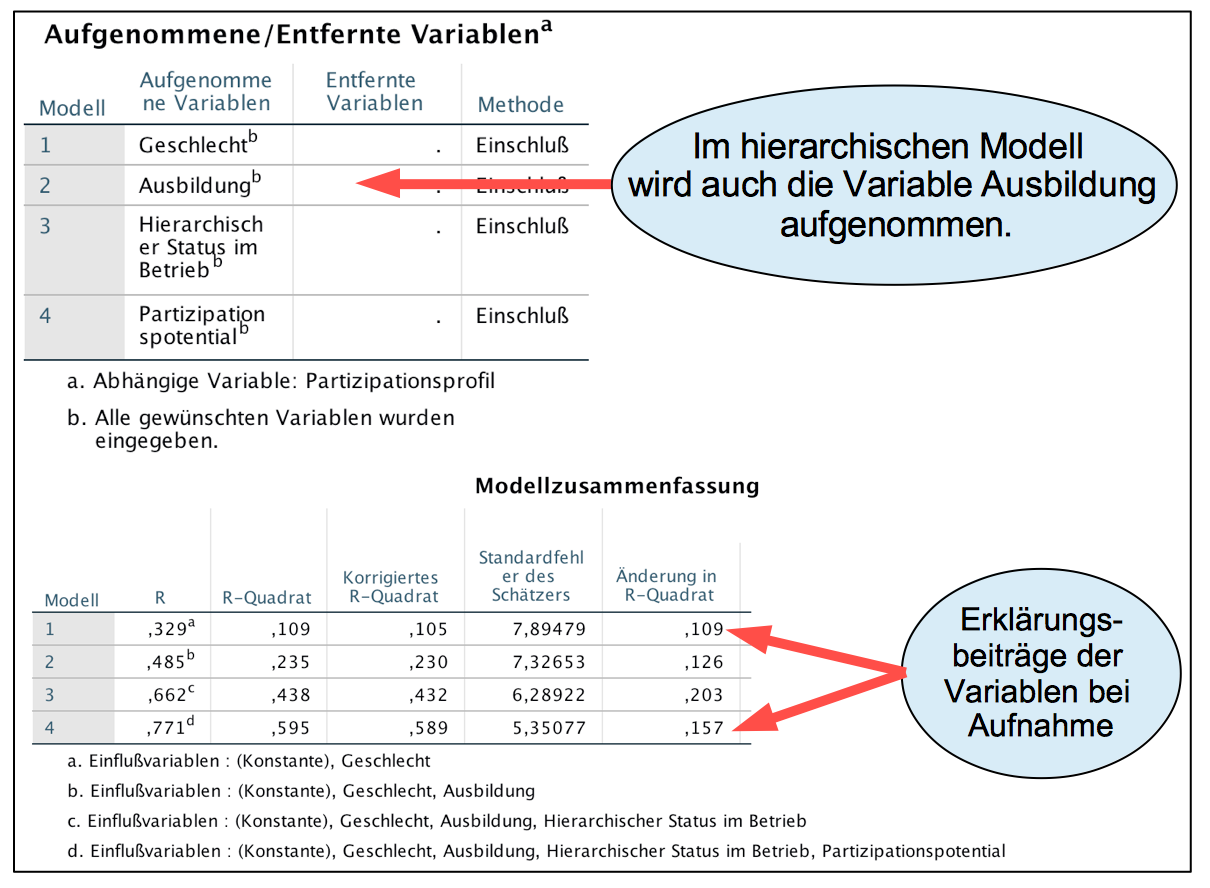
Die Modellzusammenfassung zeigt:
Die Variablen werden in der Reihenfolge: Geschlecht, Ausbildung, Status und gewünschte Beteiligung aufgenommen.
Auch der partielle Erklärungsbeitrag der Variablen Ausbildung kommt zur Geltung.
Die Änderungen in R-Quadrat liegen dabei zwischen 10 und 20%.
Der Determinationskoeffizient des hierarchischen Modells liegt ausserdem mit einem Betrag von 0,595 geringfügig über dem Wert für das schrittweise Modell von 0,594.
Screenshot 12-45: Die Anova Tabelle "hierarchisch"
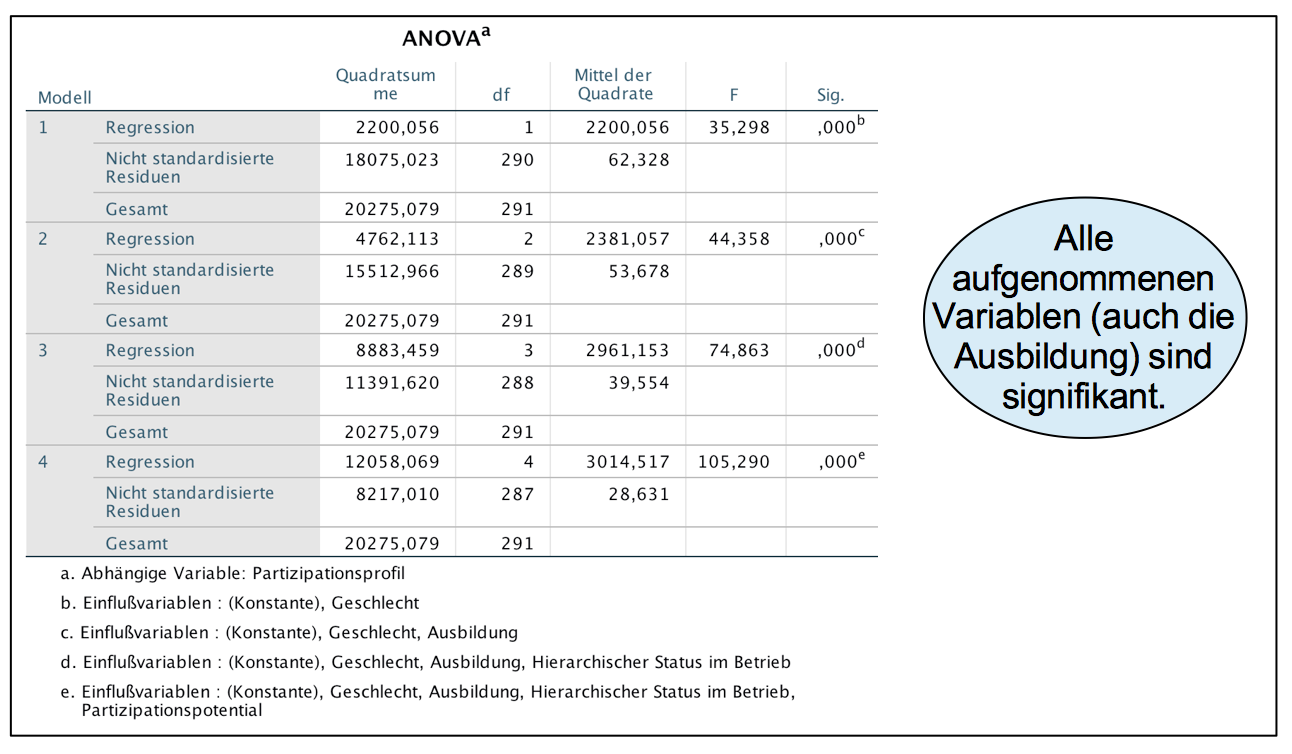
Tabelle 12-3 : Die Zurechnung der Quadratsummen (SAQ) in den hierarchischen Modellen
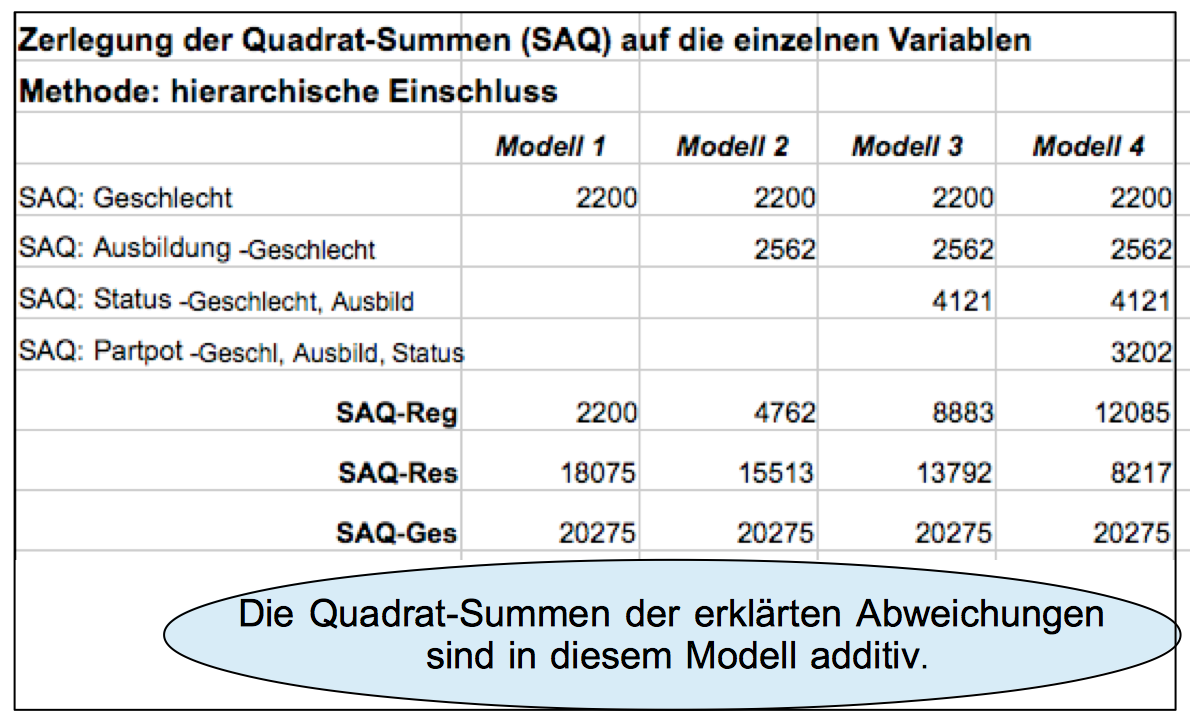
In der blockweisen Erweiterung der Modell nimmt die erklärte Summe der Abstandsquadrate (SAQ-Reg) zu, die Fehlerquadrate (SAQ-Res) reduzieren sich entsprechend.
Das Modell 4 teilt die insgesamt erklärte Summe der Abstandsquadrate auf die einzelnen Variablen entsprechend ihren Beiträgen auf.
Screenshot 12-46: Die Tabelle der partiellen Regressionskoeffizienten "hierarchisch"
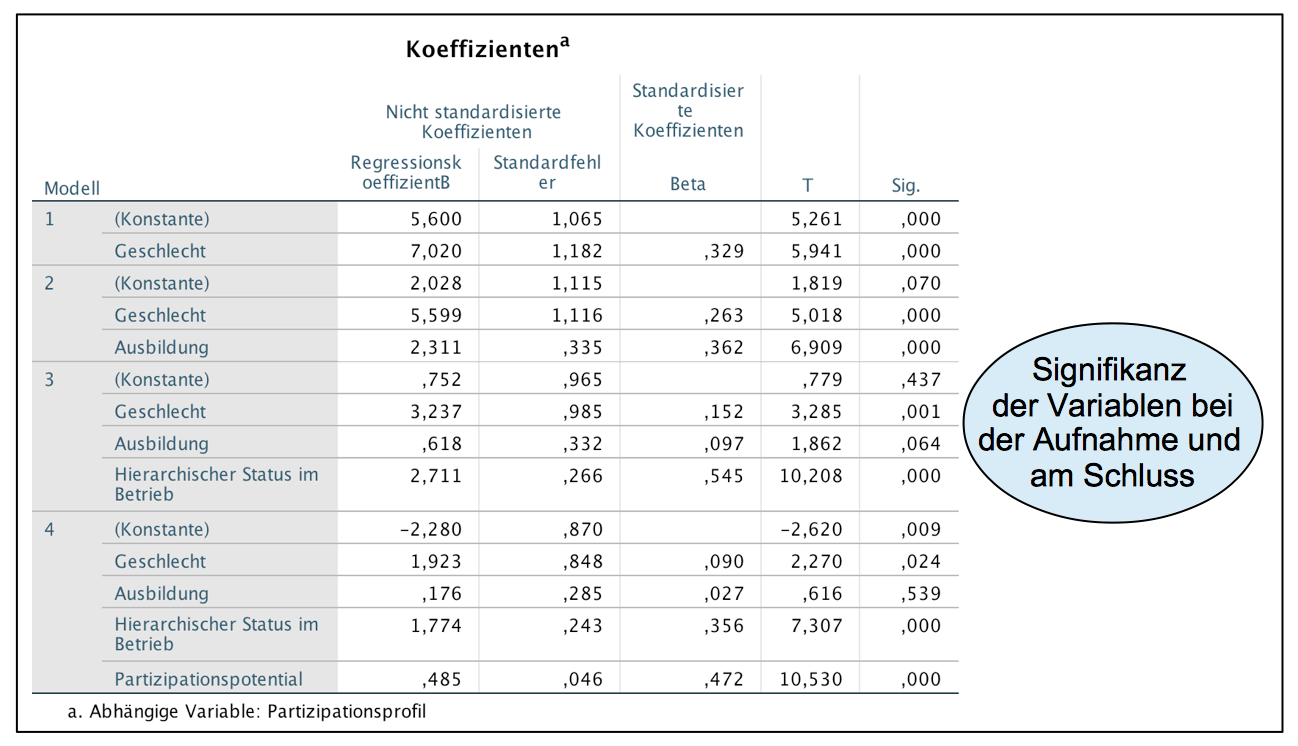
Tabelle 12-4: Die partiellen Regressionskoeffizienten bei Aufnahme und bei Abschluss
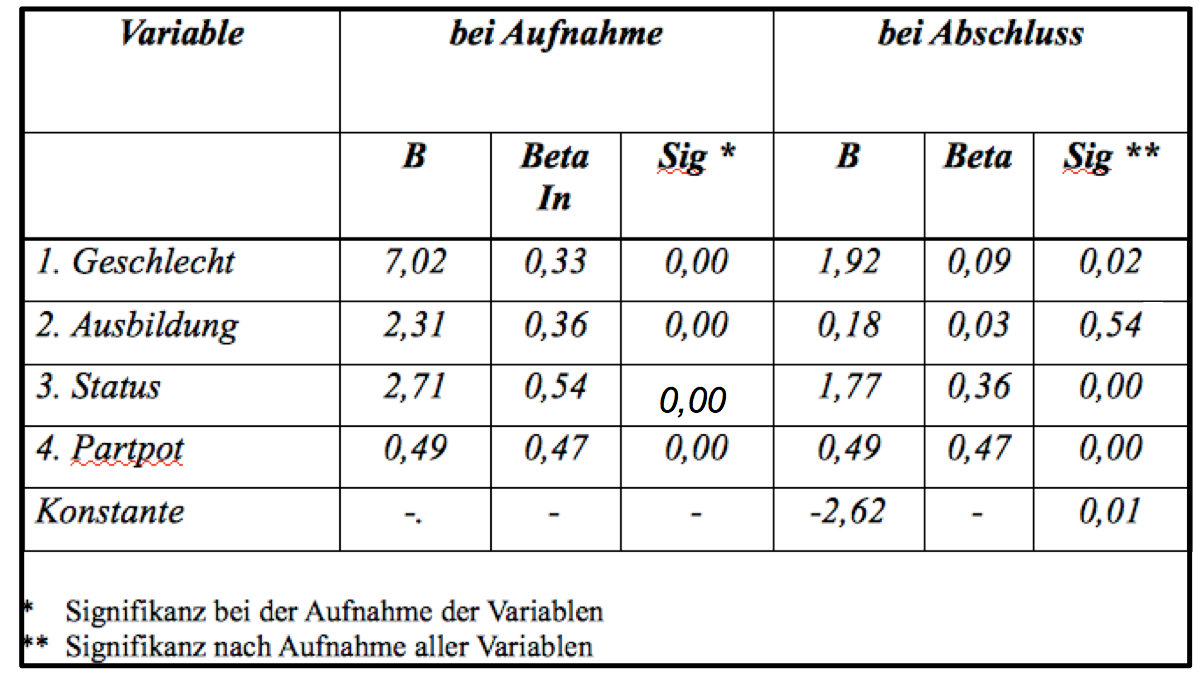
Anmerkung: Zur Darstellung und Interpretation der induktiven Aspekte der Regressios- und Korrelationsanalyse vgl. den Verweis am Ende des Abschnitts.
e) Der Vergleich der Analysemodelle
Der Erklärungsbeitrag der Variablen
Schaubild 12-3: R-Quadrat und Änderungen in R-Quadrat
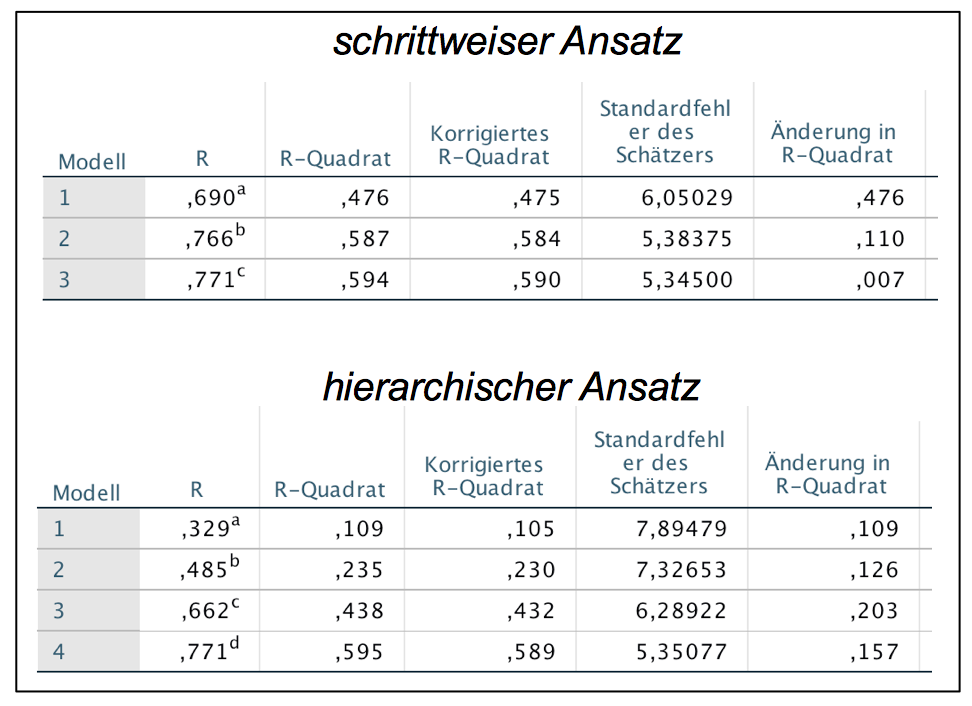
Der Erklärungsbeitrag des Gesamtmodells ist im hierarchischen Ansatz (R2 = 0,595) etwas größer als im schrittweisen Modell (R2 = 0,594).
Im schrittweisen Modell mit der Variablenreihenfolge Partizipationspotential, Status und Geschlecht werden etwa 80% der gesamten Erklärungskraft im ersten Schritt erreicht. Die Verbesserung des Modells im letzten Schritt ist nur noch sehr gering.
Im hierarchischen Modell mit der Variablenreihenfolge Geschlecht, Ausbildung, Status und Partizipationspotential tragen die einzelnen Variablen zwischen 10 - 20 % der gesamten Erklärungskraft.
Reihenfolge und Signifikanz des Einschlusses
Schaubild 12-4: Reihenfolge und Signifikanzen
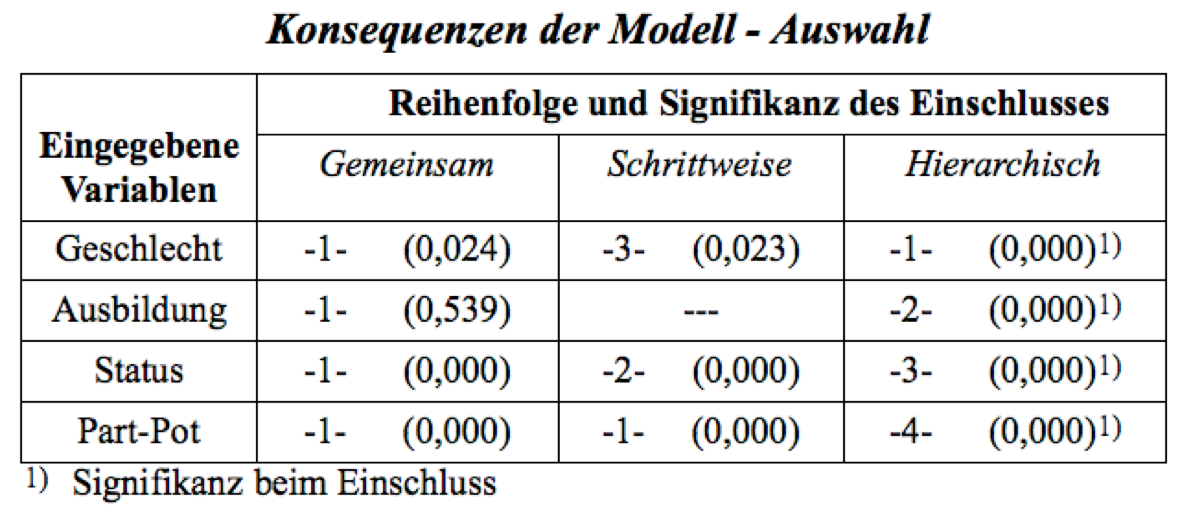
Maßgeblich für die Relevanz einer Variablen im Modell ist der ihr im Prozess zugewiesene Varianzanteil.
Signifikanzen < 0,05 signalisieren, dass die Hypothese, eine Variable leiste keinen überzufälligen Beitrag, zurückgewiesen werden muss.
In den Modellen "Einschluss" und "Schrittweise" ist der Erklärungs-Anteil bei Abschluss des Prozesses maßgeblich. Die sachlogisch relevante Variable "Ausbildung" leistet danach keinen signifikanten Beitrag.
Im "hierarchischen" Modell ist hingegen der bei der Aufnahme ins Modell zugewiesene Anteil relevant. Alle kausal-analytischen Einflussfaktoren werden aufgenommen.
Anmerkung: Eine ausführlichere Darstellung und Interpretation der induktiven Aspekte der multiplen Regressions- und Korrelationsanalyse mit SPSS findet sich in
ViLeS 2, Modul "Test der Regressions- und Korrelationskoeffizienten, Teil B"
sowie unter:
ViLeS 2, Modul "Konfidenzintervalle in der Regressions- und Korrelationsanalyse, Teil B" .
2. Aufgaben
a) Die Partizipationsdaten
Am Beispiel der Datei Partizipation_1.sav und der dort enthaltenen, metrisch-skalierten Variablen Partizipationsprofil und Partizipationspotential und den, im Folgenden als metrisch behandelten, Variablen Geschlecht, Ausbildung und Status lassen sich auch die Einflüsse dieser Variablen auf gewünschten Beteiligung aufzeigen.
Berechnen Sie den Zusammenhang zwischen der Variablen Partizipationspotential und den übrigen relevanten Variablen im Datensatz.
Wählen Sie dazu einen schrittweisen oder einen hierarchischen Ansatz oder prüfen Sie beide auf ihre Tauglichkeit.
Interpretieren Sie Ihre Ergebnisse.
b) Die Wohndaten
Analysieren Sie unter Verwendung der Datei Wohnen.sav mit SPSS die multiplen Regressions- und Korrelationszusammenhänge zwischen den Variablen Wohnfläche, Zahl der Räume, Eigentümer/Mieterstatus, Nationalität, Haushaltseinkommen und Miethöhe.
Analyse der Wohnfläche
Berechnen Sie den Zusammenhang zwischen der Wohnfläche und den Variablen Zahl der Räume, Eigentümer/Mieterstatus, Nationalität, Haushaltseinkommen und Miethöhe.
Wählen Sie dazu einen schrittweisen oder einen hierarchischen Ansatz oder prüfen Sie beide auf ihre Tauglichkeit.
Interpretieren Sie Ihre Ergebnisse.
Analyse der Miethöhe
Berechnen Sie für die Mieterhaushalte den Zusammenhang zwischen der Miethöhe und den Variablen Zahl der Räume, Wohnfläche, Nationalität und Haushaltseinkommen.
Wählen Sie auch hier einen schrittweisen oder einen hierarchischen Ansatz oder prüfen Sie beide auf ihre Tauglichkeit.
Interpretieren Sie Ihre Ergebnisse.
|



