 |
Konzepte und Definitionen im Modul XII-6 Multiple Regressions- und Korrelationsmodelle
1. Konzeptionelle Vorüberlegungen
a) Das Modell und seine Voraussetzungen
Die lineare multiple Regressions- und Korrelationsanalyse untersucht den Zusammenhang zwischen einer abhängigen metrischen Variablen X1 und einer Reihe von unabhängigen metrischen Variablen X2....... Xk .
Abb. 12-20: Die Variablenstruktur
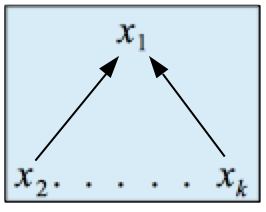
Voraussetzungen der Analyse sind somit:
einmal ein Satz von metrischen Variablen:
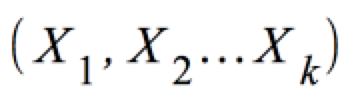
und weiter die Existenz einer Korrelationsmatrix R , d.h. dass multiple Interdependenzen in diesem Datensatz gegeben sind.
Tabelle 12-2 : Die Korrelationsmatrix R
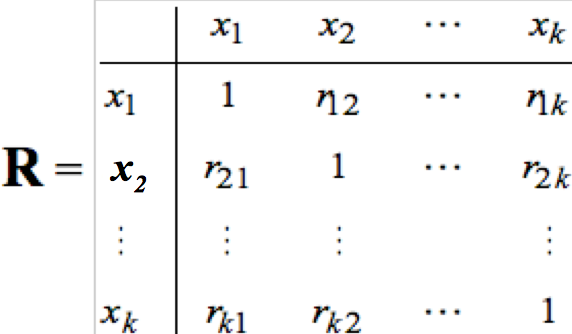
b) Zielsetzung und Modellstruktur
c) Modellvarianten und Analysestrategien
Der Einbezug der unabhängigen Variablen kann je nach Analyseziel auf folgende Weise geschehen:
Im gemeinsamen Einschluss werden alle unabhängigen Variablen in einem Block eingegeben.
Im schrittweisen Einschluss erfolgt der Einbezug der Variablen nacheinander nach einem statistischen Kriterium.
Im hierarchischen Einschluss werden die Variablen einzeln oder blockweise unter kausalen Aspekten hierarchisiert und entsprechend eingegeben.
2. Das Modell der multiplen Regressionsanalyse
a) Die Funktionsgleichung
Konkret ergeben sich die Beobachtung der abhängigen Variablen x1,i aus den Funktionswerten xc1,i und dem Fehlerterm ui . Vereinfacht dargestellt als:
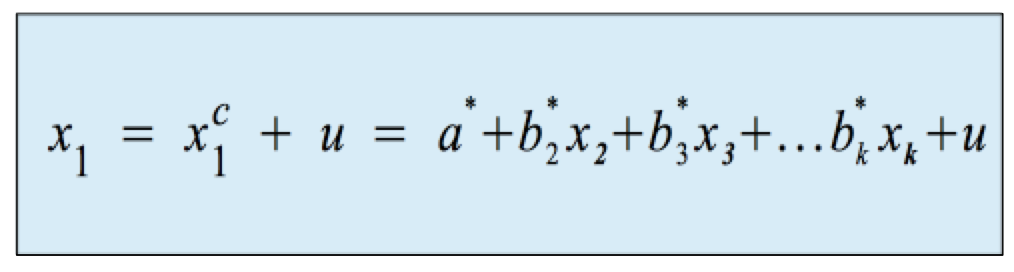
Für ein Regressionsmodell mit vier Variablen gilt also:
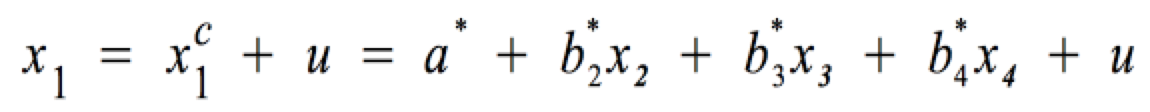
mit den multiplen Regressionskoeffizienten:
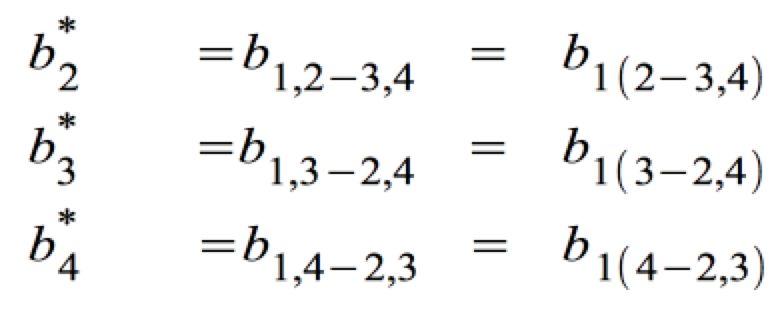
Die multiplen Regressionskoeffizienten ergeben sich als partielle/semi-partielle Regressionskoeffizienten der Variablen xj aus der die jeweils anderen unabhängigen Variablen auspartialisiert wurden.
Sie geben den Betrag an, um den die abhängige Variable xc1 zunimmt, wenn die entsprechende unabhängige Variable xj - unter Konstanz der übrigen unabhängigen Variablen - um eine Einheit wächst.
und der multiplen Regressionskonstanten
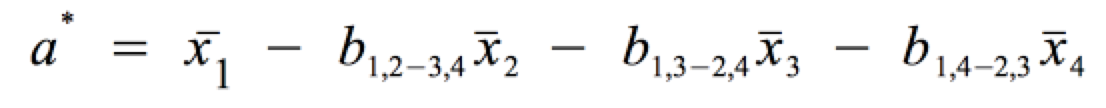
Die multiple Regressionskonstante folgt analog zur einfachen Regressionskonstanten aus der Mittelpunktsgleichung.
b) Die Methode der kleinsten Quadrate
Die Parameter der Funktionsgleichung ergeben sich (wie bei der einfachen linearen Regression) nach der Methode der kleinsten Quadrate, nach der die Regressionsfunktion als k-1-dimensionale Hyperebene so in die k-dimensionale Punktwolke eingepasst wird, dass die quadrierten Abstände der Beobachtungen von der Regressionsfunktion (die Quadratsumme der Fehler u = x1,i - xc1,i ) minimiert werden:
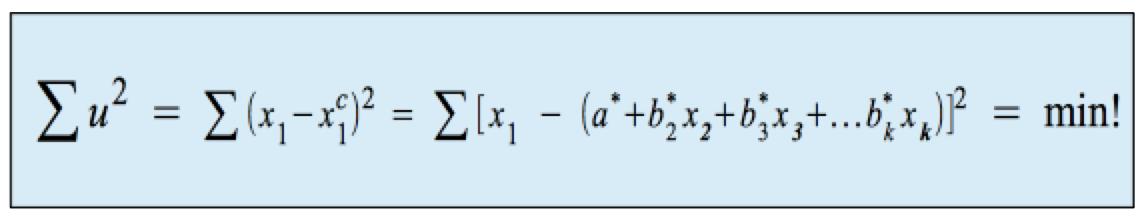
Dies wird erreicht, indem die partiellen Differentiale der Fehler-Quadratsumme nach den Koeffizienten "Null" gesetzt werden:
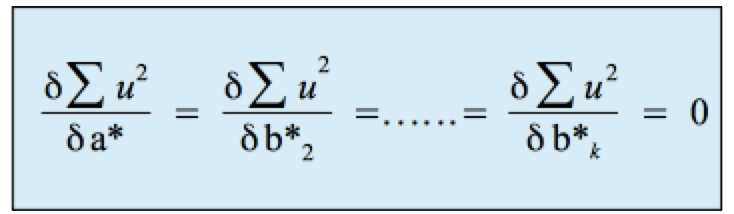
c) Die Schreibweisen der Regressionsfunktion
Die funktionale Form des Zusammenhangs lässt sich auf zwei Weisen formulieren:
-
Für die beobachteten Variablenwerte X2....... Xk erhalten wir:

-
Für die Abweichungen der beobachteten Variablenwerte X2....... Xk von ihren Mittelwerten ergibt sich nach Einsetzen von a* in obige Gleichung die Regressionsfunktion:
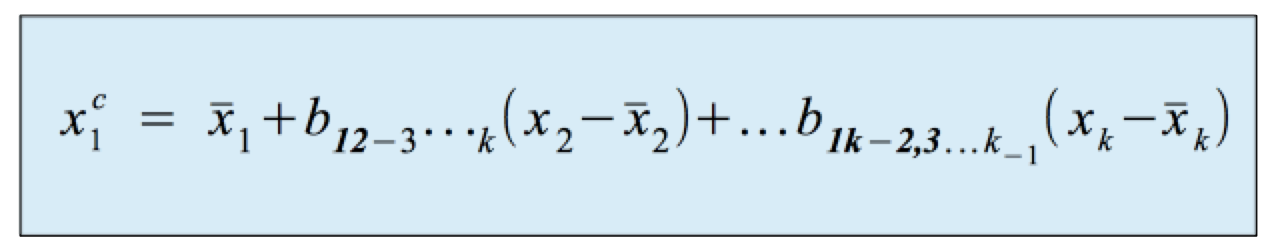
3. Das Modell der multiplen Korrelationsanalyse
a) Die Zerlegung der Gesamtvarianz
Analog zur einfachen Regressions- und Korrelationsanalyse lässt sich die Varianz der abhängigen Variablen
x1 in einen durch die Regressionsfunktion erklärten Teil und in einen nicht-erklärten Teil zerlegen:
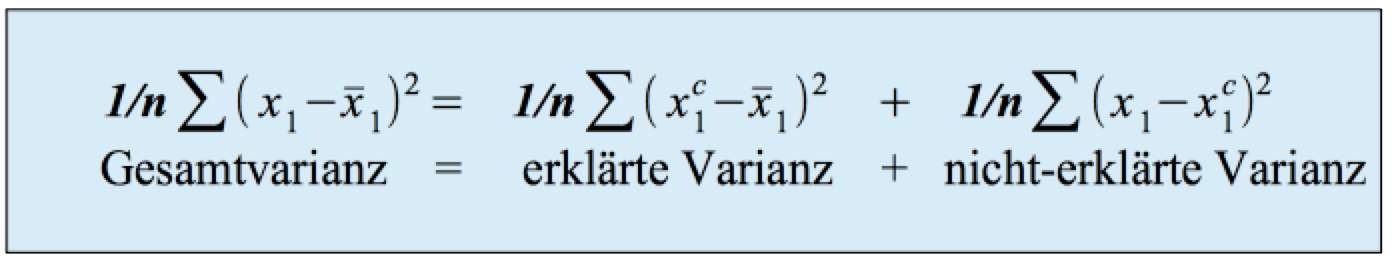
Allerdings resultiert xc1 jetzt aus der multiplen Regressionsfunktion.
b) Die Definition des multiplen Determinationskoeffizienten R2k
Wie bei der einfachen Korrelation ergibt sich der Determinationskoeffizient als Verhältnis der erklärten Varianz zur Gesamtvarianz bzw. der durch die Regressionsfunktion erklärten Summe der Abstandsquadrate zur Gesamtsumme der Abstandsquadrate:
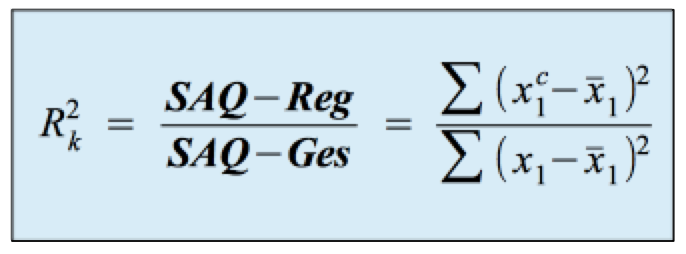
Bei Abhängigkeiten innerhalb der unabhängigen Variablen ist der multiple Determinationskoeffizient deutlich kleiner als die Summe der einfachen Determinationskoeffizienten:
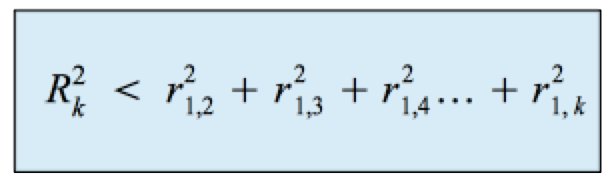
4. Strategien der Modellbildung
Unter analytischen Aspekten stehen folgende Strategien zum Einbezug der unabhängigen Variablen zur Verfügung:
Der gemeinsame Einschluss aller unabhängigen Variablen:
Alle erklärenden Variablen werden in einem Schritt einbezogen.
Damit enthält das Modell auch Variablen, die keinen signifikanten Erklärungsbeitrag liefern. Zwar werden letztere ausgewiesen, erhöhen gleichwohl, wenn auch nur geringfügig, das Ausmaß der erklärten Varianz.
Der kumulative Einschluss der unabhängigen Variablen:
Die erklärenden Variablen werden nacheinander einbezogen.
Diese Strategie erlaubt die schrittweise Verbesserung der Erklärungskraft und die Identifikation der Erklärungsbeiträge der unabhängigen Variablen nach bestimmten Kriterien.
Diese Kriterien des Einbezugs werden im nächsten Abschnitt einander gegenübergestellt.
a) Der gemeinsame Einschluss der unabhängigen Variablen
Im gemeinsame Einschluss aller Variablen werden
alle gelisteten, erklärenden Variablen kollektiv ins Modell aufgenonmmen.
Strategisch betrachtet, prüft diese Methode, welche der im Datensatz vorhandenen Variablen einen Erklärungsbeitrag leisten und welche nicht.
Die nicht-signifikanten Variablen werden in einem zweiten Schritt ausgeschlossen, so dass nur die tatsächlich relevanten Variablen in ein Erklärungsmodell Eingang finden.
Dieser Ansatz wurde bereits in den Punkten 2. und 3. behandelt.
b) Der sukzessive, kumulative Einschluss der unabhängigen Variablen
Das Konzept, die Variablen nicht in einem Zug sondern sukzessiv einzubeziehen, wird im Folgenden ohne Bezug auf das Einschluss-Kriterium vorgestellt, das die Reihenfolge der Aufnahmen regelt (vgl. dazu Punkt 5).
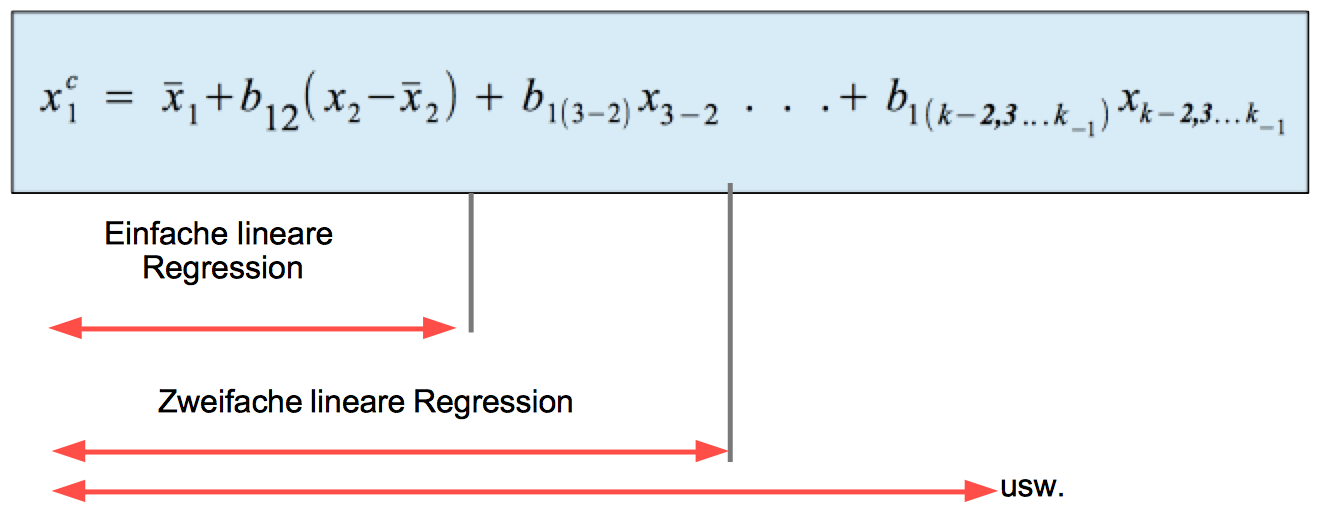
Dem kumulativen Modell liegt eine Schreibweise der multiplen Regressionsfunktion zugrunde, in der die Variable xc1 als Funktion fortschreitend höherer Partialvariablen erscheint:
Schaubild 12-2: Kumulativer Aufbau der Regressionsfunktion
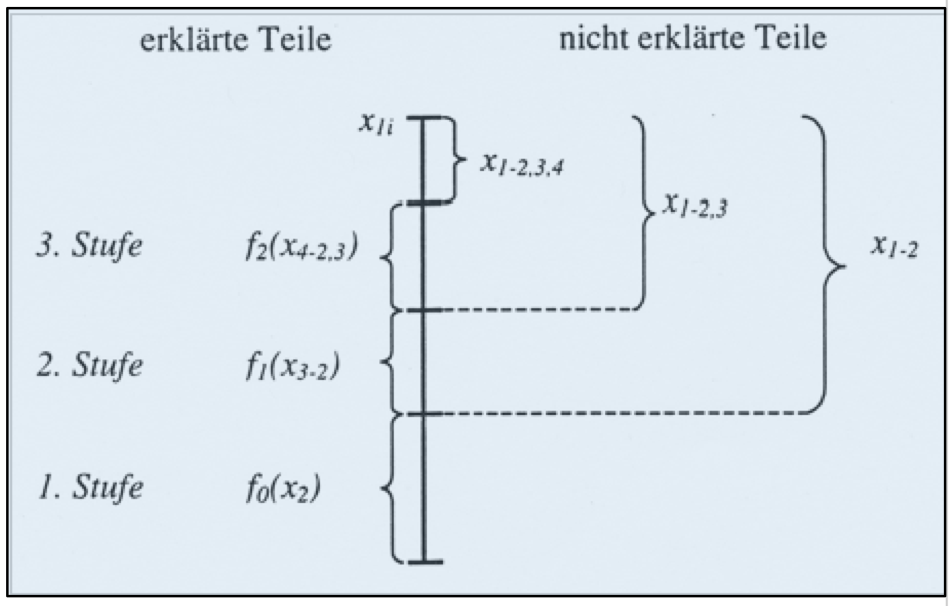
Dem kumulativen Aufbau der Funktion entspricht eine schrittweise Reduktion der Fehler:
Abb. 12-21: Erklärte und nicht erklärte Variablenteile
Der multiple Determinationskoeffizient ergibt sich so als Summe von
fortlaufend höheren, partiellen Determinationskoeffizienten.
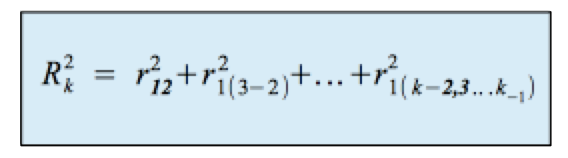
Die Veränderung des Determinationskoeffizienten wird als RSQ-Change ausgewiesen.

Diese Veränderung entspricht dem partiellen Determinationskoeffizienten
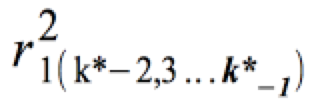 der jeweils aufgenommenen Variablen xk* .
der jeweils aufgenommenen Variablen xk* .
5. Kriterien des sukzessiven Einbezugs der unabhängigen Variablen
Die verschiedenen Konzepte zum Einbezug der unabhängigen Variable sollen am konkreten Beispiel der Einflussfaktoren auf die individuelle Beteiligung an betrieblichen Entscheidungsprozessen veranschaulicht werden.
Dazu werden die im Partizipations-Datensatz vorliegenden Variablen tatsächliche Beteiligung, Geschlecht, Bildungsniveau, beruflicher Status und gewünschte Beteiligung in die Analyse eingebracht.
a) Der formale Einschluss der unabhängigen Variablen nach der Höhe des Erklärungsbeitrags
Der schrittweise Aufbau des Regressionsmodells wird in diesem Ansatz durch den, bei jedem Schritt gegebenen höchsten partiellen Korrelationskoeffizienten bestimmt.
Als erste Variable wird die Variable mit dem höchsten einfachen Korrelationskoeffizienten (partieller Korrelationskoeffizient "nullter Ordnung") ausgewählt.
Im zweiten Schritt folgt die Variable mit dem höchsten partiellen Korrelationskoeffizient "erster Ordnung", usw..
Aus der Korrelationsmatrix (vgl. Kap. XI-3, Screenshot 11-14) ergibt sich:
dass die Variable "gewünschte Beteiligung" am stärksten mit der tatsächlichen Beteiligung korreliert ist. Diese Variable würde bei der Erklärung der tatsächlichen Beteiligung im schrittweisen Modus als erste ins Modell aufgenommen, obwohl der Zusammenhang eher umgekehrt ist, d.h. dass die gewünschte von der tatsächlichen Beteiligung bestimmt wird.
Als nächste Variable würde vermutlich der betriebliche Status aufgenommen, allerdings als Partialvariable, aus der der Einfluss der gewünschten Beteiligung auspartialisiert wurde. Auch hier ist der Zusammenhang zwischen beiden Variablen
eher umgekehrt.
Die Präsentation des schrittweisen Ansatzes im nächsten Modul weist die Variable "Geschlecht" als nächste Variable aus, wobei die Einflüsse der gewünschten Beteiligung und des Status, ebenfalls entgegen der kausalen Logik, vorher eliminiert wurden.
In der Beispielsrechnungen wird die Variable "Ausbildung" als Partialvariable 3. Ordnung nicht mehr berücksichtigt, da ihre vielfältigen Einflüsse alle den anderen Variablen subsummiert wurden.
b) Der hierarchische Einschluss der unabhängigen Variablen
Im Kausal-Modell werden die im Partizipations-Datensatz vorliegenden Variablen Geschlecht, Bildungsniveau, beruflicher Status und gewünschte Beteiligung in eine Hierarchie der Abhängigkeiten eingebracht:
Abb. 12-22: Hierarchisches Modell zur Erklärung des Beteiligungsniveaus
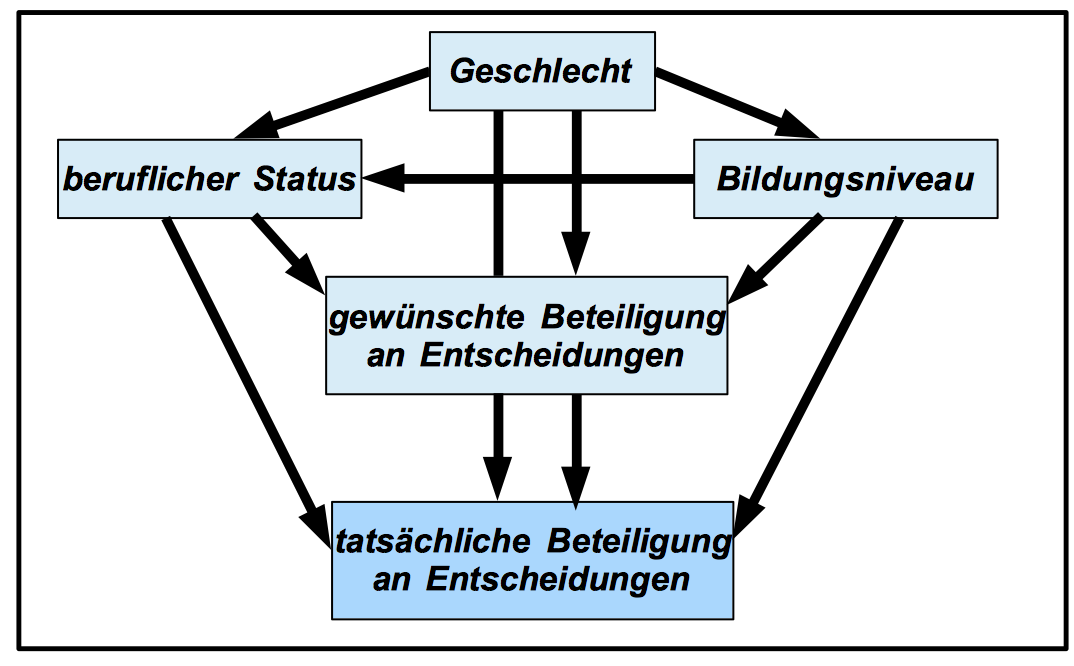
In kausaler Hinsicht ist die Variable "Geschlecht" die unabhängigste im Variablensatz und wäre deshalb als erste zu berücksichtigen.
Als nächstes kommt die Variable "Ausbildung" zur Geltung, soweit sie zusätzlich zur Variable "Geschlecht" einen Erklärungsbeitrag leistet.
Als Partialvariable 2. Ordnung wird danach der betriebliche Status aufgenommen und schließlich - bereinigt um die Persönlichkeitsvariablen - ist auch der Einfluss des persönlichen Interesses am Entscheidungsprozess nicht zu vernachlässigen.
c) Formale vs. kausale Modellkonstruktion
Die Auswirkungen der beiden Kriterien zur Aufnahme der Variablen auf die Modellkonstruktion lassen sich anhand der folgenden Grafiken veranschaulichen.
Die grafische Veranschaulichung des einfachen Determinationskoeffizienten:
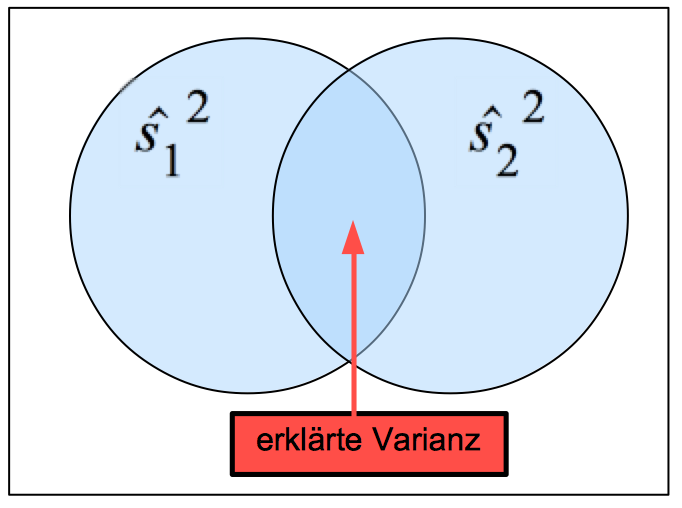
Dazu betrachten wir die gemeinsame Varianz zweier standardisierter Variablen Z1 und Z2 als Ausdruck der Stärke einer Korrelationsbeziehung. Aus dem Modul XII-2 ist bekannt, dass die Determinationskoeffizienten der Ausgangsvariablen und der standardisierten Variablen identisch sind.
Standardisierte Variablen weisen eine Varianz von "Eins" auf. Diese Varianzen lassen sich durch Kreise darstellen, deren Fläche gleich "Eins" gesetzt wird und deren gemeinsame "erklärte" Varianz der Überschneidung der beide Kreise entspricht. Der Determinationskoeffizient als Verhältnis der erklärten Varianz zur Gesamtvarianz ist in folgendem Schaubild als Schnittfläche skizziert:
Abb. 12-23: Die gemeinsame Varianz zweier standardisierter Variablen Z1 und Z2
Die Zurechnung der gemeinsamen partiellen Varianzen nach dem statistischen Kriterium
Beim sukzessiven Einbezug der Variablen nach dem jeweils größten partiellen Korrelationskoeffizienten wird den unabhängigen Variablen am Ende jeweils nur ihr partieller Beitrag in der Größe der schwarzen Segmente zugeordnet. Die grau-schraffierten Segmente werden keiner der unabhängigen Variablen angerechnet. Dies kann dazu führen, dass einige Variablen wegen eines zu geringen Beitrags nicht im Modell berücksichtigt werden.
Abb. 12-24: Die Zurechnung der gemeinsamen Varianzen nach dem statistischen Kriterium
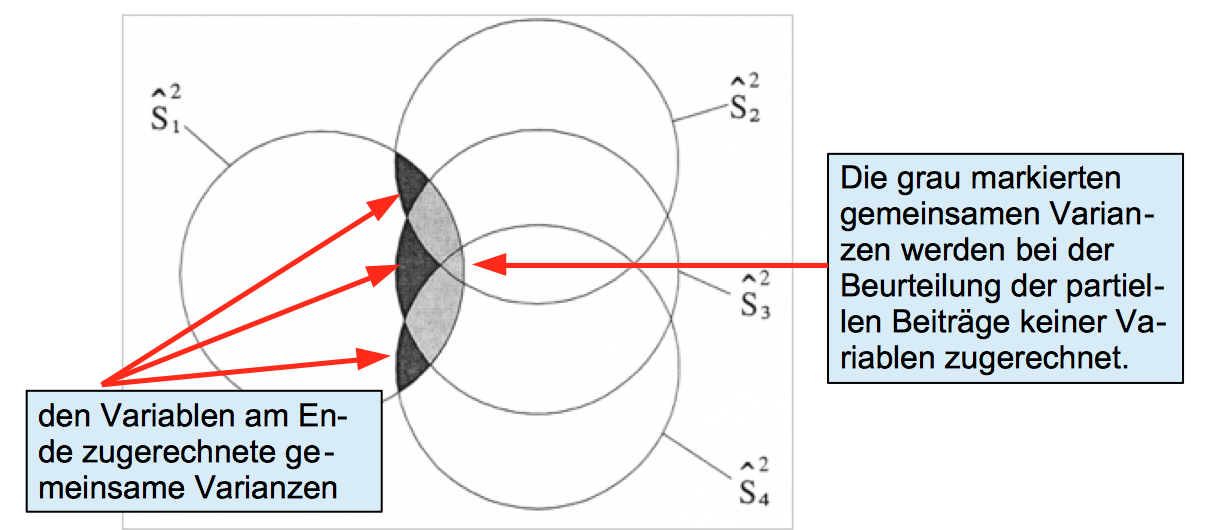
Dies ist neben der unter Punkt 4. demonstrierten unlogischen Reihenfolge der Aufnahme der Variablen eine weitere analytischen Konsequenz dieses Verfahrens.
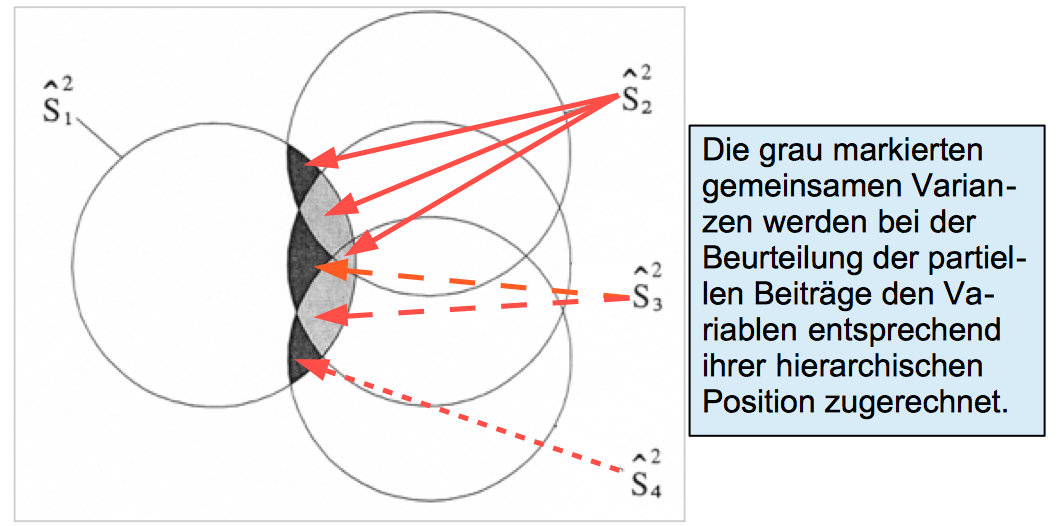
Die Zurechnung der gemeinsamen partiellen Varianzen nach dem kausal-analytischen Kriterium
Die obigen Probleme stellen sich beim schrittweisen Einbezug der Variablen im hierarchischen Modell nicht, da (vgl. Abb. 11-25) der Variablen Z2 alle drei mit der Variablen Z1 gemeinsamen Segmente, der Variablen Z3 die darunter liegenden zwei Segmente und der Variablen Z4 das verbleibende schwarze Segment zugesprochen wird.
Abb. 12-25: Die Zurechnung der gemeinsamen Varianzen nach dem kausal-analytischen Kriterium
Der multiple Determinationskoeffizient ergibt sich entsprechend der Formel in 4.b) als Summe von
fortlaufend höheren, partiellen Determinationskoeffizienten.
Fazit
Das hierarchisch/kausal-analytische Modell erfordert eine Vorab-Festlegung der kausalen Strukturen im Datensatz.
Es berücksichtigt beim Modellaufbau nicht nur die logischen Zusammenhänge innerhalb der unabhängigen Variablen.
Es enthält darüber hinaus meist mehr erklärende Variablen und weist deshalb i.A. insgesamt einen etwas höheren Determinationskoeffizienten auf.
Das formal/statistische Modell vernachlässigt Variablen mit geringen Erklärungsbeiträgen und ist deshalb bei einer etwas geringeren Gesamterklärung effizienter.
Es entwickelt sich nach einem impliziten quantitativem Kriterium und wird deshalb i.A. automatisierten Data-Mining-Prozessen zu Grunde gelegt.
Allerdings sagt das Ergebnis nichts über die kausale Relevanz der einzelnen unabhängigen Variablen aus, deshalb sollten diese auch nicht als "erklärende" Variablen missverstanden werden.
Ein rechnerischer Vergleich der Modell anhand der Partizipationsvariablen der Abb. 12-22 findet sich im nächsten Arbeitsschritt "Beispiele und Aufgaben".
Anmerkung: Eine ausführlichere Darstellung und Interpretation der induktiven Aspekte der multiplen Regressions- und Korrelationsanalyse findet sich in
ViLeS 2, Modul "Test der Regressions- und Korrelationskoeffizienten, Teil B" sowie unter
ViLeS 2, Modul "Konfidenzintervalle in der Regressions- und Korrelationsanalyse, Teil B" .
|



