 |
Einfaktorielle Varianzanalysen mit SPSS - Beispiele und Aufgaben im Modul XII-5 Die einfaktorielle Varianzanalyse
1. Beispielsrechnungen mit SPSS
SPSS bietet mit dem Modul "Analysieren > Mittelwerte vergleichen > Mittelwerte.." und dem Tool "Analysieren > Mittelwerte vergleichen > Einfaktorielle ANOVA.." zwei Tools zur einfaktoriellen Varianzanalyse an. Diese beiden Tools überschneiden sich in den Analysen teilweise, behandeln aber auch jeweils unterschiedliche Aspekte der Varianzanalyse
Die Beispielsrechnungen werden mit den Daten der Datei Partizipation_1.sav und der dort enthaltenen, metrisch-skalierten Variablen "Partizipationsprofil" sowie der jetzt explizit als nicht-metrisch behandelten Kontrollvariablen "Status" graphisch veranschaulicht und rechnerisch durchgeführt.
Dabei soll u.a. im Vergleich zu den bisherigen Zusammenhangsanaylsen auf der Basis unterstellter metrischer Skalierung der Variable Status geprüft werden, ob und wie weit der Zusammenhang zwischen der tatsächlichen Beteiligung und dem Status durch die (korrekte) Behandlung dieser Kontrollvariablen als ordinaler Faktor beeinflusst wird und welche Veränderungen sich im Hinblick auf die Stärke des Zusammenhangs ergeben.
a) Das Tool "Analysieren > Mittelwerte vergleichen > Mittelwerte.."
Die Analysekomponenten des Tools "Mittelwerte..."
Mit dem Tool werden:
zum Einen die im Schaubild 12-2 (vgl. Modul "Konzepte und Definitionen") angesprochenen Gruppenmittelwerte, Gruppengrößen und Streuungsparameter der Gruppen präsentierte. Damit wird ein erster Eindruck vermittelt, ob sich die Verteilungen in den einzelnen Gruppen wesentlich unterscheiden.
zum Zweiten werden in der ANOVA-Tabelle die SAQ-gesamt, die SAQ-zwischen und die SAQ-innerhalb sowie die entsprechenden Varianzen präsentiert. Dabei wird die SAQ-zwischen aufgeteilt in einen Anteil, der durch die Annahme der Linearität erklärt werden kann und welcher der Abweichung der Mittelwerte von der Linearität zuzuschreiben ist.
Auf der Basis dieser Komponenten werden drittens R und R 2 sowie η und η2 berechnet und einander gegegnübergestellt.
Der Aufruf des Tools "Mittelwerte..."
Die beiden folgenden Screenshots zeigen, wie das Tool aufzurufen ist:
|
Screenshot 12-24: Die Anforderung des Tool
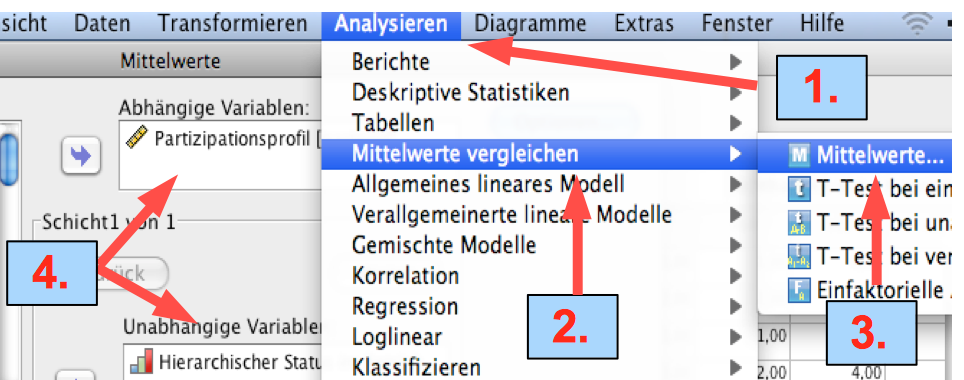
1: Analysieren aufrufen
2: "Mittelwerte vergleichen“ auswählen,
3: "Mittelwerte" konkretisieren,
4: "partpot" und "Status"eingeben.
|
|
Screenshot 12-25: Die Spezifizierung des Tools
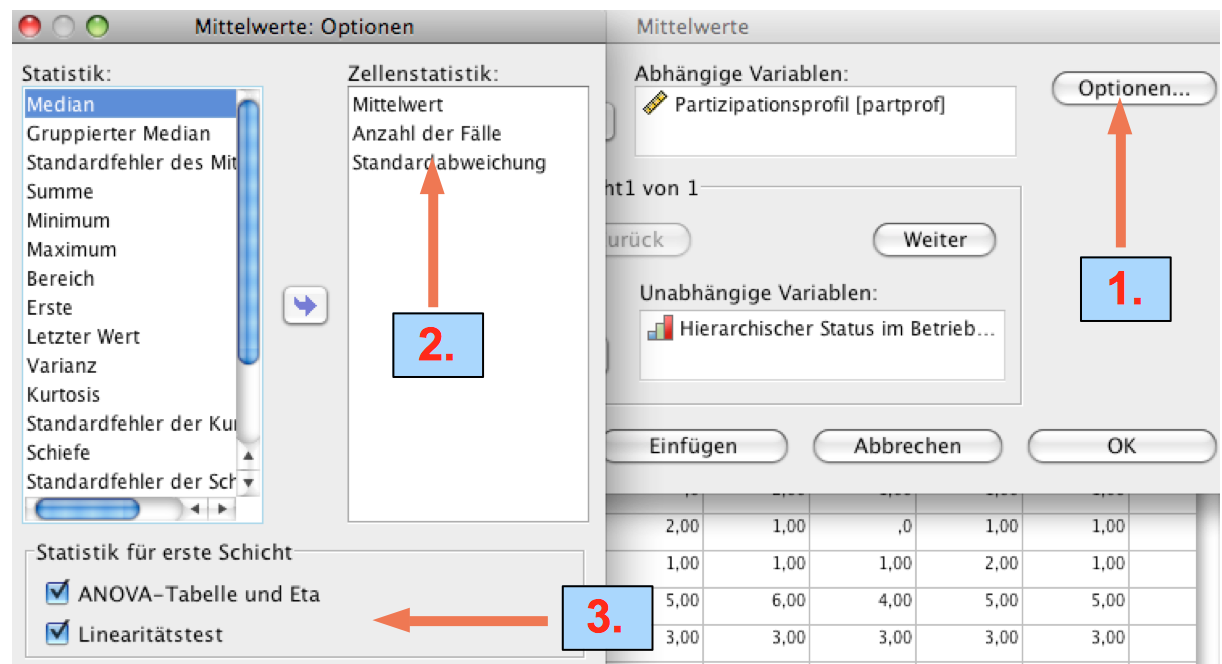
1: "Optionen" wählen,
2: Zellenstatistiken definieren
3. die ANOVA-Tabelle und den Linearitätstest anfordern.
|
|
|
Der Output des Tools "Mittelwerte..."
|
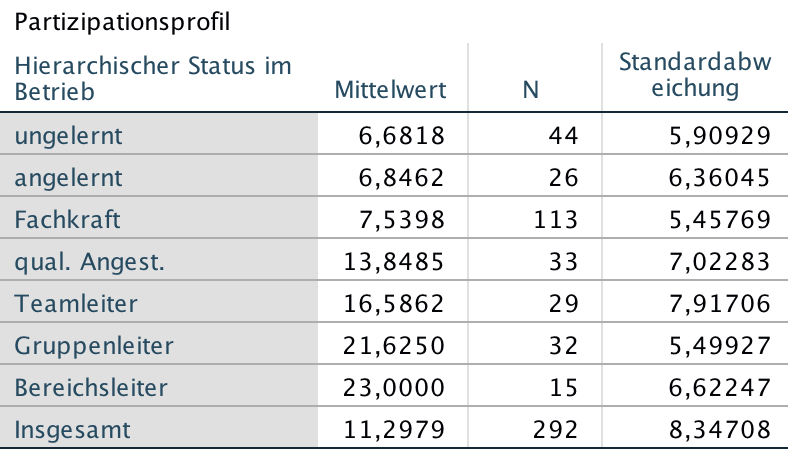
Screenshot 12-26: Die Zellenstatistiken
|
|
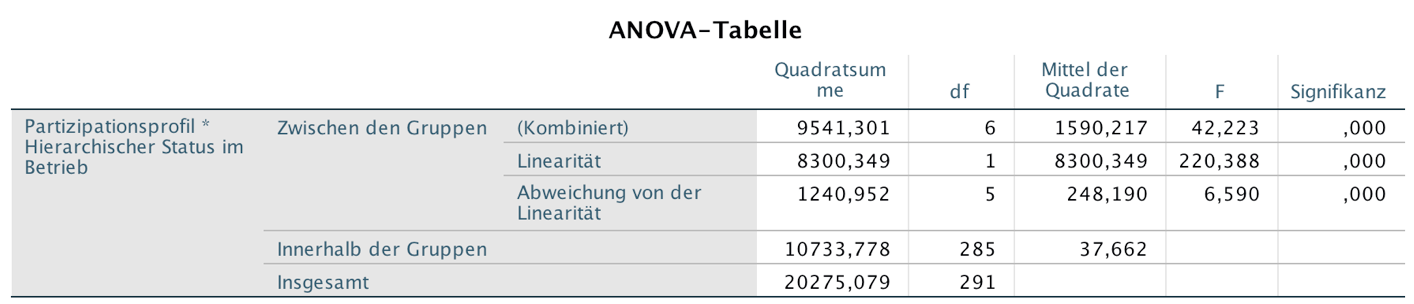
Screenshot 12-27: Die ANOVA-Tabelle
|
|
|
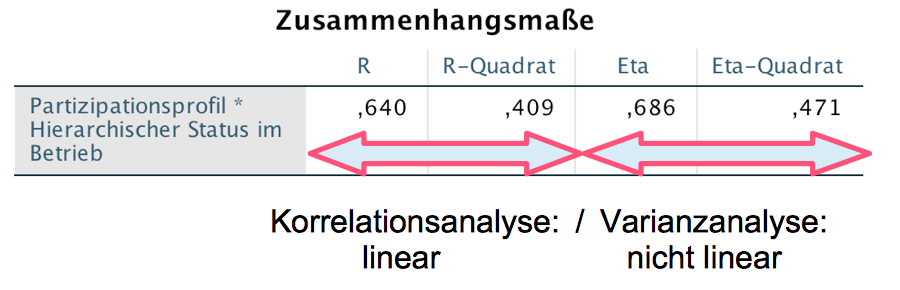
Screenshot 12-28: Die Zusammenhangsmaße
Die Interpretation der Ergebnisse"
Als Ergebnis kann festgehalten werden, dass:
Die Mittelwerte der Beteiligung der einzelnen Statusgruppen an den Entscheidungsprozessen unterscheiden sich deutlich mit einem Wert von etwa 7 für die statusniedrigsten Gruppen und von etwa 22 für die höchsten. Das entsprechende Mittelwert-Diagramm wird vom Tool "Einfaktorielle ANOVA" produziert (vgl. Punkt b).
Gleichzeitig wird aber deutlich, dass sich nicht alle Gruppenmittelwerte von einander unterscheiden. Auch dies wird mit dem Tool "Einfaktorielle ANOVA - Kontrastgruppen-Analyse" weiter untersucht.
Die ausgewiesenen Standardabweichungen in den Gruppen liegen zwischen etwa 5,5 und 7,9.
Die Stärke des Zusammenhangs zwischen der tatsächlichen Beteiligung und dem Status ist mit einem η2 von 0,47 nochmals gegenüber dem R-Quadrat von 0.41 aus der linearen (und gegenüber einem Wert von 0,44 aus der quadratischen) Korrelationsanalyse angestiegen.
Die, diesen Ergebnissen zugrunde liegenden SAQ-Beträge werden in der ANOVA-Tabelle ausgewiesen. Die Abweichung von der Linearität sind signifikant und anhand des Mittelwert-Diagramms auch nachzuvollziehen.
b) Das Tool "Analysieren > Mittelwerte vergleichen > Einfaktorielle Varianzanalyse"
Die Analysekomponenten des Tools "Einfaktorielle Varianzanalyse."
Mit dem Tool werden:
zum Einen nochmals die Gruppenmittelwerte und die Streuungsparameter der Gruppen präsentierte (hier nicht wiedergegeben).
Die Mittelwerte werden im Mittelwert-Diagramm in Form eines Linienzuges veranschaulicht.
In der Tabelle zur Levene-Statistik wird ein Test zur Homogenität der Varianzen präsentiert. Die Homogenität der Varianzen ist die Voraussetzung für den Test der Mittelwert-Differenzen und die Kontrastgruppenanalyse.
In der ANOVA-Tabelle finden sich wieder die SAQ-gesamt, die SAQ-zwischen und die SAQ-innerhalb sowie die entsprechenden Varianzen. Das entsprechende η2 wird in diesem Tool nicht ausgewiesen.
Der Aufruf des Tools "Einfaktorielle ANOVA"
Die beiden folgenden Screenshots zeigen, wie das Tool aufzurufen ist:
|
Screenshot 12-29: Die Analyseoptionen spezifizieren
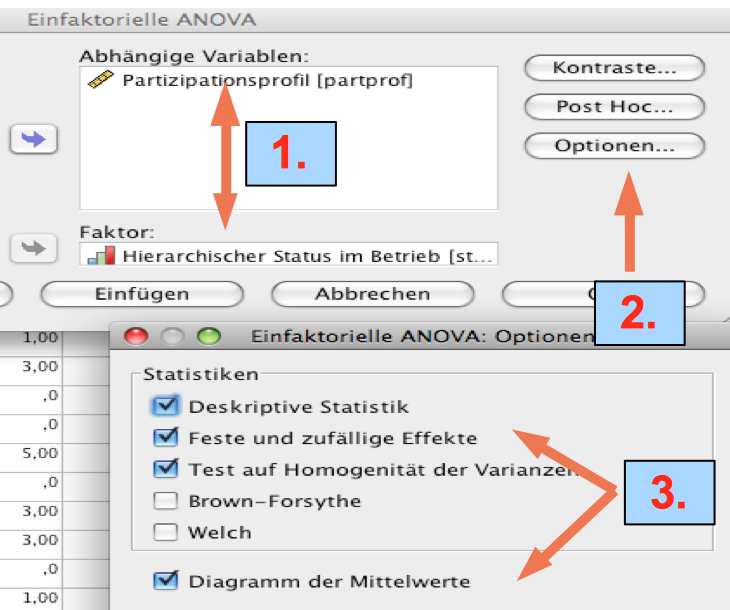
"Einfaktorielle Anova“ entsprechend Screenshot 12-24 aufrufen,
1: "partpot" und "Status"eingeben,
2: "Optionen" auswählen,
3: "Optionen" konkretisieren.
|
|
Screenshot 12-30: Die Kontrastgruppen-Analyse anfordern
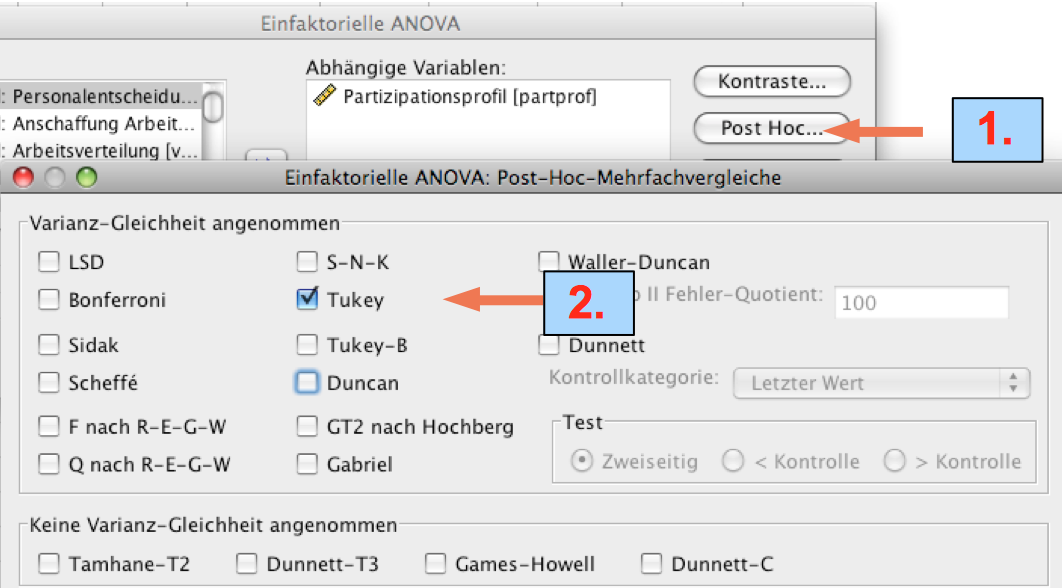
1: "post hoc Mehrfachvergleiche" wählen,
2: "Tukey"- Test anfordern
Anmerkung: Unter den verschiedenen Testvarianten wird hier der am häufigsten eingesetzte Test vorgeschlagen.
|
|
|
Der Output des Tools "Einfaktorielle ANOVA"
|
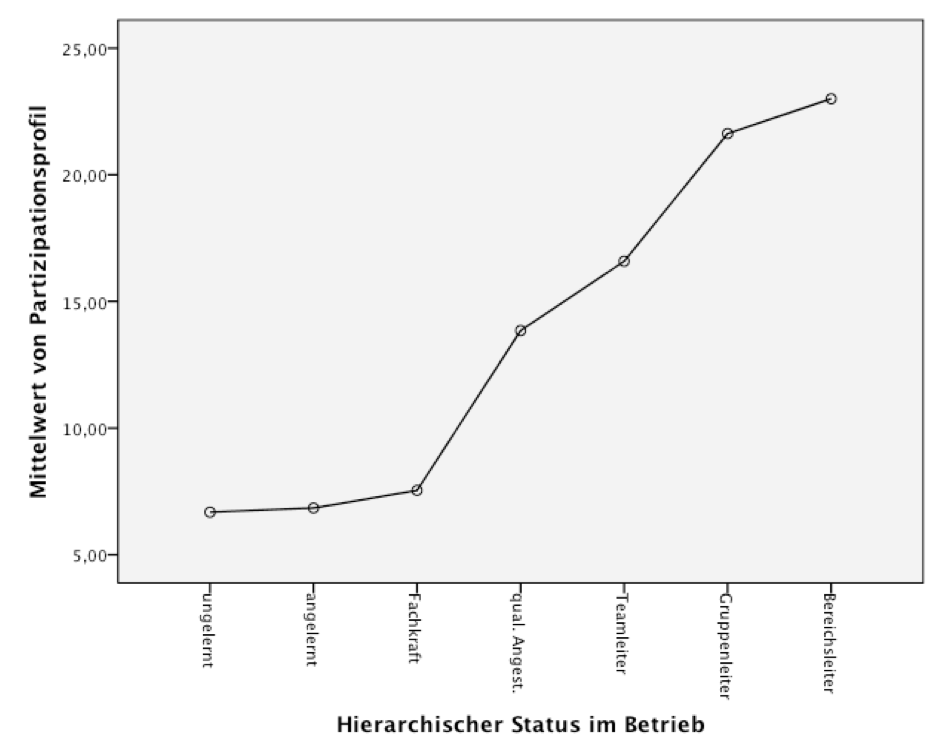
Screenshot 12-31: Das Mittelwert-Diagramm
|
|
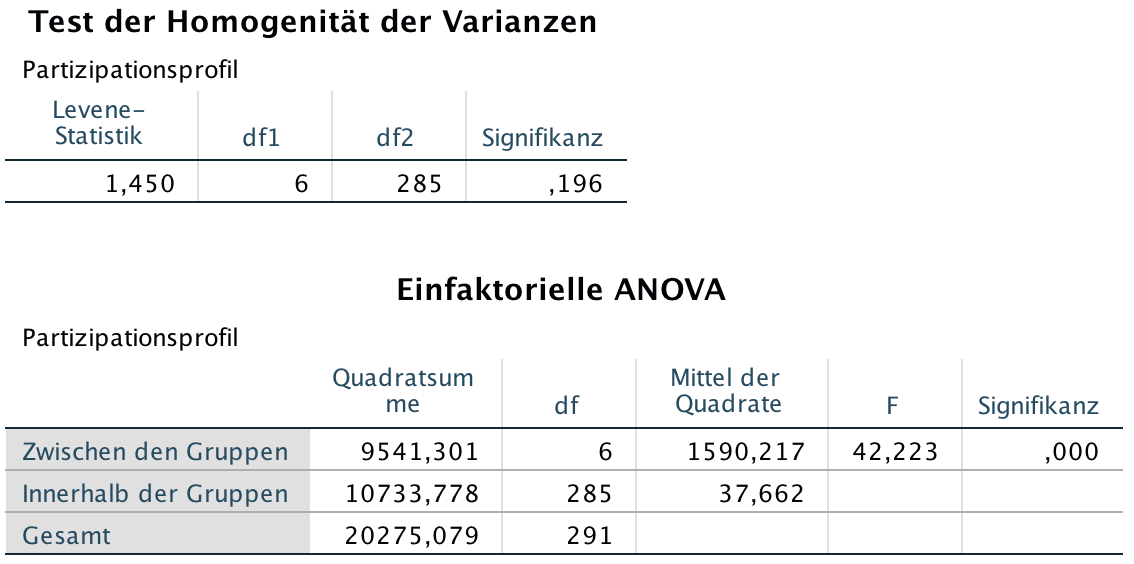
Screenshot 12-32: Der Test auf Homogenität der Varianzen
und die "ONEWAY ANOVA"
|
|
|
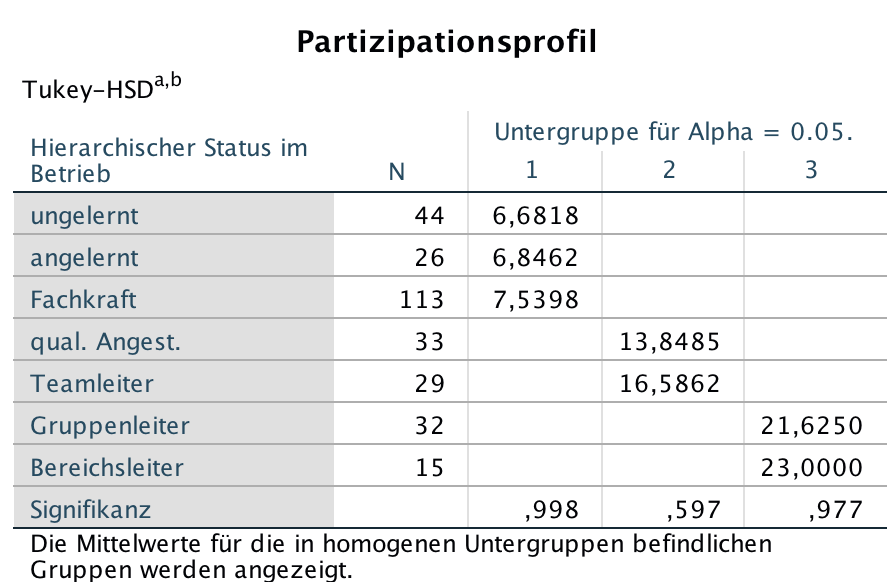
Screenshot 12-33: Die homogenen Untergruppen
Die Interpretation der Ergebnisse
Als Ergebnis kann festgehalten werden:
Die Mittelwerte der einzelnen Statusgruppen unterscheiden sich deutlich. Ihr Verlauf wird im Mittelwert-Diagramm grafisch dargestellt.
Gleichzeitig ist zu sehen, dass der Verlauf nicht linear ist und dass sich nicht alle Gruppenmittelwerte von einander unterscheiden. Dieser Aspekt wird mit der Kontrastgruppen-Analyse weiter untersucht.
In Abb.: 12-32 werden der Levene-Test auf Homogenität der Varianzen und die ANOVA-Tabelle präsentiert:
Die ausgewiesenen Standardabweichungen in den Gruppen liegen zwischen etwa 5,5 und 7,9. Bei einer Signifikanz von 0,196 und einem Signifikanzniveau von 0.01 kann die Hypothese, die Varianzen in den Gruppen seien nur zufällig unterschiedlich, nicht zurückgewiesen werden.
Die Werte der ANOVA-Tabelle entsprechen denen des Screenshots 12-28.
Die Stärke des Zusammenhangs zwischen der tatsächlichen Beteiligung und dem Status wird mit diesem Tool nicht berechnet.
Die Kontrastgruppenanalyse in 12-33 weist drei jeweils homogene Untergruppen auf. Auch hier wird die Hypothese homogener Mittelwerte in den Gruppen mit Signifikanzen von 0,998, 0,597 und 0,977 deutlich bestätigt.
Anmerkung: Darstellung und Interpretation der induktiven Aspekte der Testansätze finden sich in ViLeS 2, Allgemeine Aspekte des Testmodells
und speziell für die Varianzanalyse in
Teil C (Exkurs): Die Tests der η2-Koeffizienten in der ein- und mehrfaktoriellen Varianzanalyse
2. Aufgaben
Die Beispielsrechnungen haben gezeigt, dass die zentralen Aspekte einer einfaktoriellen Varianzanalyse nur mit den beiden Tools "Mittelwerte..." und "Einfaktorielle ANOVA" angesprochen werden können. Es wird deshalb empfohlen zur Bearbeitung der folgenden Aufgaben beide Tools einzusetzen.
a) Die Ausgangsdaten
Zum Vergleich mit den obigen Beispielsrechnungen zum Zusammenhang zwischen tatsächlicher Beteiligung und betrieblichem Status können Sie unter Verwendung der Datei Partizipation_1.sav mit SPSS eine einfaktorielle Varianzanalyse zwischen den Variablen Partizipationsprofil und der Ausbildung durchführen.
Dieser Analyse können Sie danach eine Untersuchung der Zusammenhänge zwischen der gewünschten Beteiligung (Variable partpot) und den Faktoren Status und Ausbildung gegenüberstellen.
b) Die Aufgabenstellung
|



