1. Die varianzanalytischen Modelle

a) Die Modellstruktur

• Die Varianzanalyse untersucht den Zusammenhang zwischen einer abhängigen metrischen Variablen und unabhängigen nicht metrischen (nominal- oder ordinalskalierten) Variablen.

• Nominal- oder ordinalskalierte Variablen können z.B. sein:

  • das Geschlecht,

  • das Ausbildungsniveau,

  • der Familienstand oder

  • die Stellung im Beruf.

b) Die unabhängigen Variablen

• Die unabhängigen Variablen werden i.A. als Faktoren bezeichnet (nicht zu verwechseln mit den Komponenten der Faktorenanalyse, die ebenfalls als Faktoren bezeichnet werden):

• Wir bezeichnen die abhängige Variable wieder mit x₁ und die Faktoren mit Großbuchstaben (A, B,..) und ihre Ausprägungen mit j,l, ... Allgemein also:
  
  

c) Die ein- und die mehrfaktorielle Varianzanalyse

• Besteht das varianzanalytische Modell nur aus einer abhängigen und einer unabhängigen Variablen, sprechen wir von einer einfaktoriellen Varianzanalyse.
  Wird zur Erklärung der abhängigen Variablen eine Mehrzahl von unabhängigen Faktoren herangezogen, liegt eine mehrfaktorielle Varianzanalyse vor.

• Konkret ergeben sich:
  
  

• Die einfaktorielle Varianzanalyse wird im Folgenden behandelt, die mehrfaktorielle in Kap. XII-7.

2. Graphische und tabellarische Ansätze zur einfaktoriellen Varianzanalyse

• Ein einfaches Beispiel einer einfaktoriellen Analyse untersucht den Zusammenhang zwischen dem Einkommen und dem Ausbildungsniveau (gemessen in den Stufen: Hauptschulabschluss, Mittlere Reife, Abitur).

• Untersucht wird dabei die Abhängigkeit des Einkommens von der Ausbildung mit der Vermutung, dass sich die Einkommensverteilungen der drei Gruppen deutlich von einander unterscheiden und dass sich diese Unterschiede sowohl graphisch wie tabellarisch feststellen lassen.

a) Die graphische Veranschaulichung des Modellansatzes

• Wir formulieren zuerst die funktionale Form des Zusammenhangs und präsentieren danach dessen graphische Konkretisierung:

• Abbildung 12-17: Modell und graphische Veranschaulichung
  
  

b) Die tabellarische Veranschaulichung des Modellansatzes

• Schaubild 12-1: Die tabellarische Veranschaulichung
  

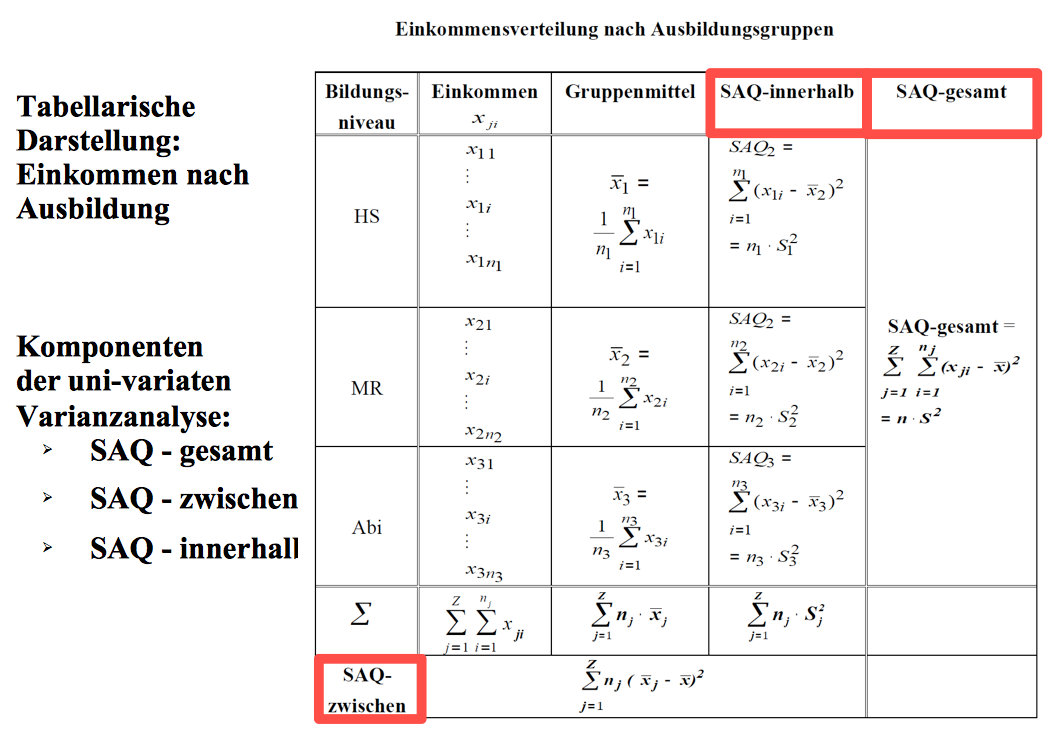
• Die Interpretation der Tabelleninhalte

  Das Schaubild präsentiert folgende statistische Angaben, aus denen die Komponenten des varianzanalytischen Modells abgeleitet werden:

  • In der Tabelle der Einkommensverteilung nach Ausbildungsgruppen beinhalten die beiden ersten Spalten die Merkmalskategorien und die Einkommensverteilungen der Gruppen.

  • In Spalte drei werden die Gruppen-Mittelwerte (also die Durchschnittseinkommen in den Gruppen) ausgewiesen.

  • In der vierten Spalte finden sich Angaben zur Streuung der Einkommen in den Gruppen in Form der Summe der Abstandsquadrate innerhalb der Gruppen (SAQ-innerhalb).

  • In der letzten Spalte findet sich die Angabe zur Gesamtsumme der Abstandsquadrate (SAQ-gesamt).

  • In der letzten Zeile komplettiert die Summe der Abstandsquadrate der Gruppenmittel zum Gesamtmittel (SAQ-zwischen) die Verteilungs-Informationen.

3. Die Modellkomponenten der einfaktoriellen Varianzanalyse

a) Die Bedeutung der Modellkomponenten

• Die SAQ-gesamt: Die SAQ-gesamt drückt die Streuung der einzelnen Einkommen um das Durchschnittseinkommen aller Einkommensbezieher in Form des n-fachen Werts der Gesamtvarianz aus.

• Die SAQ-zwischen: Diese SAQ erfasst die Streuung der Gruppenmittel um das Gesamtmittel und ist Ausdruck der ausbildungsbedingten Einkommensunterschiede.

• Die SAQ-innerhalb: Die SAQ-innerhalb erfasst die Einkommensunterschiede innerhalb der Gruppen und damit die nicht bildungsabhängigen Einkommensunterschiede.

b) Die Formeln für die Varianzkomponenten

c) Die graphische Darstellung der Varianzkomponenten

Abbildung 12-18: Graphische Veranschaulichung der Varianzkomponenten

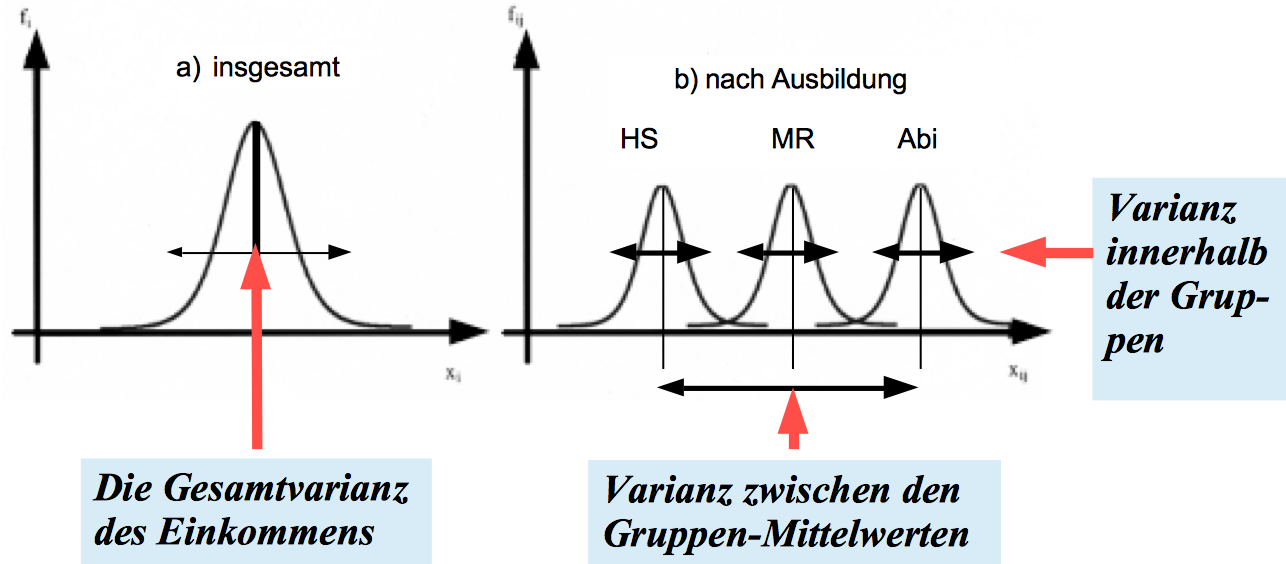
d) Der Zusammenhang der Komponenten

Der Zusammenhang ergibt sich aus der Formel:

e) Der Vergleich der Varianzanalyse mit der Korrelationsanalyse

• Die Varianzzerlegung in der Varianzanalyse entspricht der Varianzzerlegung in der Regressions- und Korrelationanalyse.

• Dort wurde die Gesamtvarianz aufgeteilt in eine durch die Regressionsfunktion bedingte Varianz und eine residuelle Varianz der Streuung der Beobachtungen um die Regressionsfunktion.

• Beide Varianzzerlegungen entsprechen einander der Form nach:
  
  1/n SAQ-Gesamt = 1/n SAQ-zwischen + 1/n SAQ–innerhalb
  ≡
  1/n SAQ-Gesamt = 1/n SAQ-reg + 1/n SAQ-res

• Somit lassen sich die Varianzkomponenten der Varianzanalyse auch als (durch die Mittelwertunterschiede) erklärte Varianz und nichterklärte Varianz innerhalb der Gruppen bezeichnen.

• Es gilt als auch für die Varianzanalyse die Formulierung:
  
  1/n SAQ-Gesamt = 1/n SAQ-zwischen + 1/n SAQ–innerhalb
  ≡
  1/n SAQ-Gesamt = 1/n SAQ-erklärt + 1/n SAQ–nicht-erklärt

4. Regressions- und Korrelationsaspekte der einfaktoriellen Varianzanalyse

a) Die Art des Zusammenhangs in der Varianzanalyse

• In der Regressionsanalyse wird die Art des Zusammenhangs durch die Form der Regressionsfunktion bestimmt.

• In der Varianzanalyse lässt sich eine "Richtung des Zusammenhangs" allenfalls durch ein sog. Mittelwert-Diagramm angeben:
  
  

  Abbildung 12-19: Das Mittelwertdiagramm der Varianzanalyse
  
  

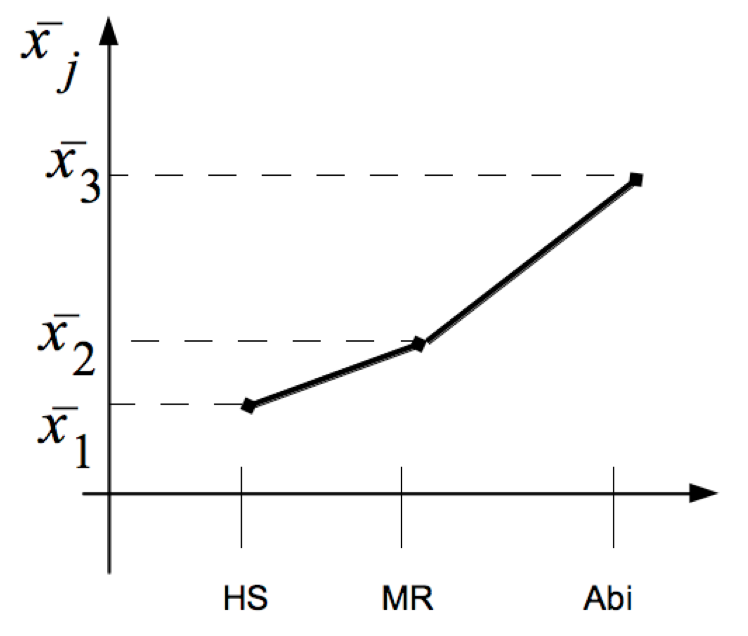
• In der konkreten Analyse lässt sich statistisch prüfen, wie sich das Ergebnis durch den nichtlinearen Verlauf der Linie gegenüber einem linearen Verlauf verbessert.

b) Die Stärke des Zusammenhangs in der Varianzanalyse

• In der Korrelationsanalyse wird die Stärke des Zusammenhangs durch den Korrelations- bzw. den Determinationskoeffizienten R² ausgedrückt. Dieser war als Verhältnis der erklärten Varianz zur Gesamtvarianz definiert.

• Analog dazu wird der Koeffizient eta-Quadrat als Maß der Stärke des Zusammenhangs in der Varianzanalyse definiert.

• Die folgende Formel für η ² (eta-Quadrat) basiert auf den entsprechende Summen der Abstandsquadraten:
  
  

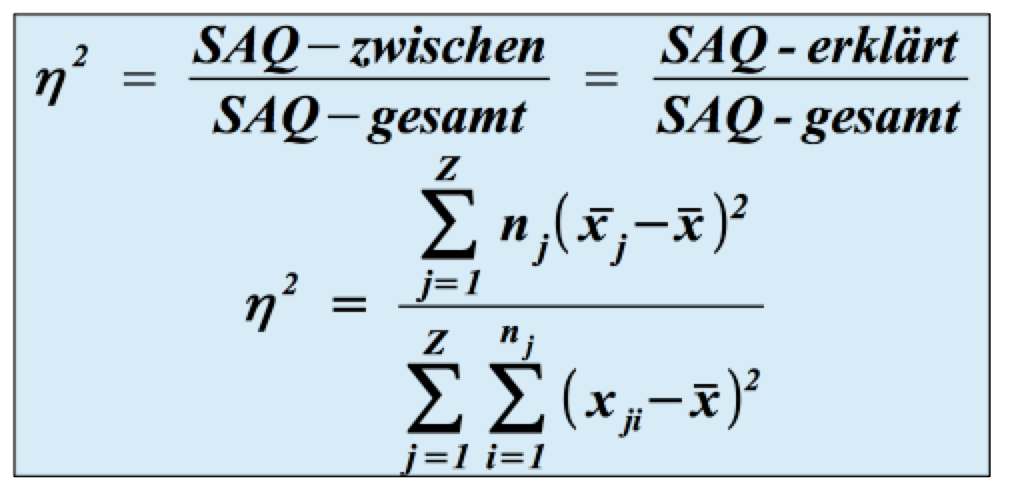
• Es gilt: 0 ≤ η² ≤ 1

5. Die Analyse der Kontrastgruppen

a) Die Funktion der Kontrastgruppen-Analyse

• Mit der Kontrastgruppenanalyse kann untersucht werden, ob sich für den Faktor - im Hinblick auf die zu erklärende Variable - homogene Untergruppen bilden lassen, also ob sich etwa A₁ und A₂ in ihren Wirkungen auf x₁ nicht unterscheiden lassen, sich aber von einer weiteren homogenen Gruppe von A₃, A₄ und A₅ deutlich abheben.

• Durch die Zusammenfassung der Merkmale und durch die Gegenüberstellung der homogene Gruppen wird die Analyse übersichtlicher und die relevanten Aspekte der Einflussnahme werden deutlicher herausgearbeitet.
  

• Der Aspekt, homogene Gruppen zusammen zu fassen, ist vor allem dann bedeutsam, wenn die ordinale oder nominale unabhängige Variable sehr viel Ausprägungen aufweist.

b) Die Definition eines Kontrastes

• Ein Kontrast D ist eine Linearkombination der Mittelwerte der Gruppen. Die Gewichte c_j ergeben sich entsprechend der Elemente in den Gruppen so, dass ihre Summe "Null" ergibt. Für das obige Beispiel also:
  
  

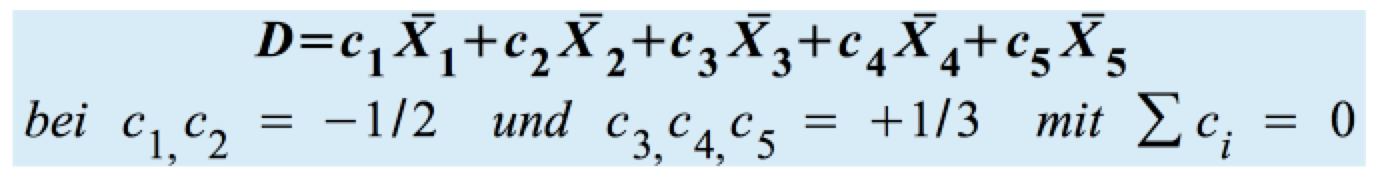
• Als weitere Bedingung wird verlangt, dass die Kontraste unabhängig von einander sind, d.h. ihre Kovarianz ist "Null".

c) Das Ergebnis der Kontrastgruppen-Analyse

• Für den Fall, dass die Mittelwerte der neu gebildeten Gruppen gleich sind, nimmt D den Wert von "Null" an.

• Weitere Aspekte der Kontrastgruppenanalyse werden im nächsten Abschnitt anhand der Beispielsrechnungen angesprochen.

Hinweis zur Navigation, zum Ausdrucken und zur Bewertung: In der Abschusszeile finden Sie einen Link zur Druckversion, zum vorherigen und zum nächsten Arbeitsschritt und mit der Sitemap eine Übersicht über das gesamte Angebot. Zur Bewertung: Diese Seite ist überarbeitet worden. Deshalb wurden die bisherigen Bewertungen gelöscht. Bewerten Sie bitte diese aktualisierte Seite neu und helfen Sie uns, damit dieses Angebot weiter zu verbessern: Diese Seite ist: sehr gut    gut    eher gut    mittelmäßig    eher schlecht    schlecht    sehr schlecht Diese Seite wurde von 1 Benutzer mit "sehr schlecht" bewertet.

1/2 50 % Fortschritt

| Feedback | Copyright | Übersicht | Druckversion | Log-Out | Sitemap | Nächster Arbeitsschritt |