 |
Partielle Regression und Korrelation mit SPSS - Beispiele und Aufgaben im Modul XII-4 Partielle Regressions- und Korrelationsmodelle
1. Beispielsrechnungen mit SPSS
SPSS bietet mit dem Modul "Analysen > Korrelation > Partiell.." nur ein Tool zur ein- und mehrfachen partiellen Korrelation explizit an (vgl. dazu Punkt b). Allerdings lassen sich einfache partielle Regressions- und Korrelationsanalysen in zwei Schritten auch mit dem Modul "Analysieren > Regression > Linear" durchführen. Diese Möglichkeit wird unter a) aufgezeigt.
Die Beispielsrechnungen werden mit den Daten der Datei Partizipation_1.sav und den dort enthaltenen, metrisch-skalierten Variablen "Partizipationsprofil" und "Partizipationspotential" sowie den (bisher noch) als metrisch behandelten Kontrollvariablen "Status", "Ausbildung" und "Geschlecht" graphisch veranschaulicht und rechnerisch durchgeführt.
Dabei soll geprüft werden, wie weit der Zusammenhang zwischen der gewünschten und der tatsächlichen Beteiligung durch diese Kontrollvariablen beeinflusst wird und welche Veränderungen sich im Hinblick auf Richtung und Stärke des Zusammenhangs der beiden Variablen ergeben, wenn der Einfluss der persönlichen Merkmale ausgeschaltet wird.
a) Die einfache partielle Regressions- und Korrelationsanalyse mit dem Tool "Regression"
Anhand der obigen Daten soll nachstehend geprüft werden, wie sich der Zusammenhang zwischen den Variablen Partizipationspotential und Partizipationsprofil verändert, wenn die Variable "betrieblicher Status" auspartialisiert (konstant gehalten) wird.
Um diese Analyse durchführen zu können, sind die Ausgangsvariablen zuerst mit der Statusvariable zu korrelieren und dabei die jeweiligen Fehlervariablen abzuspeichern. Diese Prozedur ist im Screenshot 12-21 dargestellt.
Im nächsten Schritt kann der Zusammenhang zwischen den dabei erzeugten Variablen Res_1 (= Partpot - Status ) und Res_2 (= Partprof - Status ) graphisch und rechnerisch analysiert werden. Die Ergebnisse dieser Analyse werden im Screenshot 12-22 präsentiert,
|
Screenshot 12-21: Kontrolle der Ausgangsvariablen mit SPSS
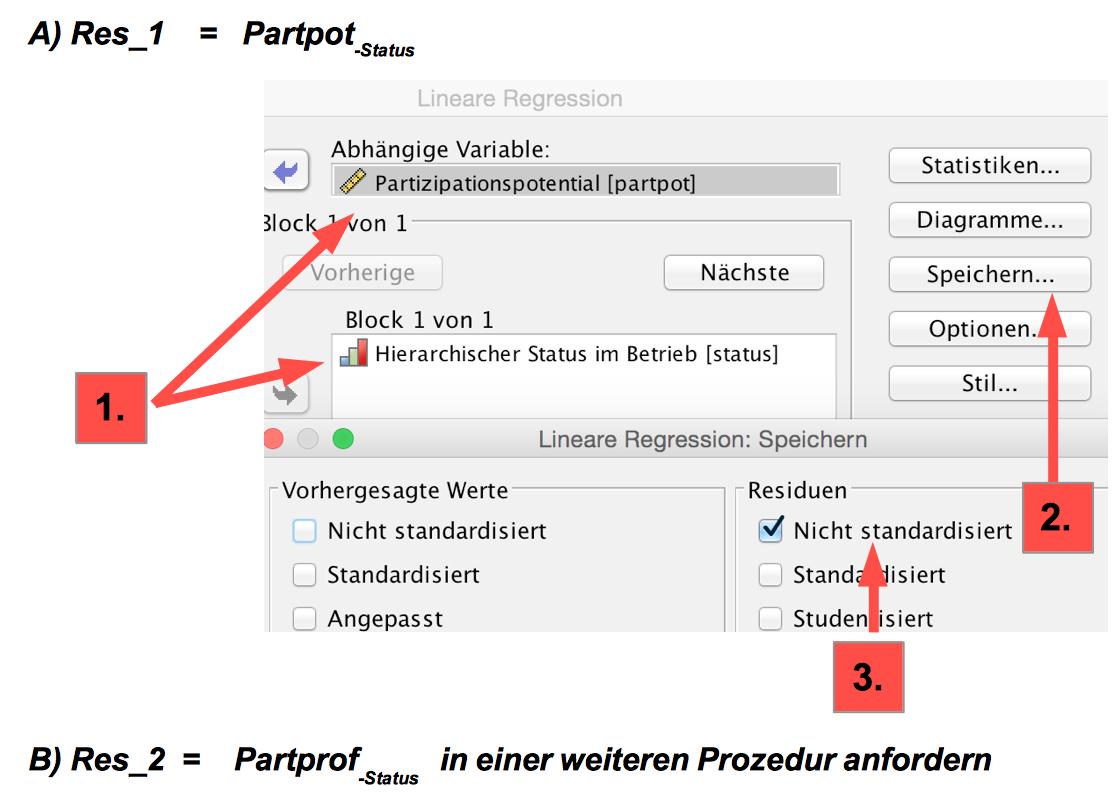
A-1: Eingabe der Variablen "partpot" und "Status",
A-2: "Speichern“ auswählen,
A-3: "Nicht standardisierte Residuen" spezifizieren,
B-1...B-3: Die Prozedur für die Variable "partprof" wiederholen.
|
|
Screenshot 12-22: Graphische und rechnerische Ergebnisse zur einfachen partielle Regression und Korrelation
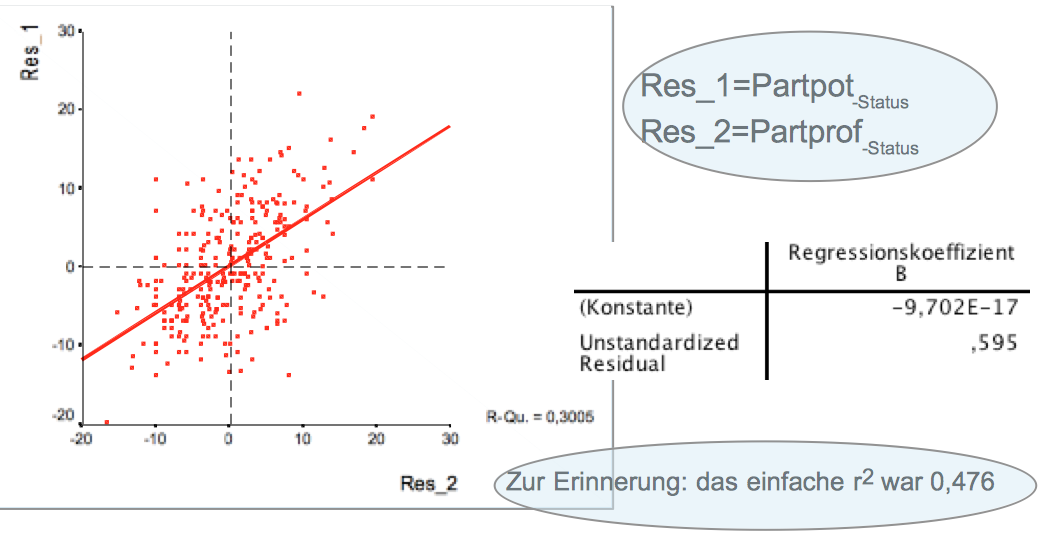
Die Grafik wurde erstellt über"Grafik>Alte Dialogfelder>Streu- / Punktediagramm>Einfaches Streudiagramm" und Eingabe der Variablen Res_1 und Res_2 und im Grafikeditor bearbeitet (zum Verfahren vgl. Kap. 11-3).
Die Rechnung wurde mit dem Tool "Analysieren>Regression" durchgeführt.
|
|
|
Als Ergebnis kann festgehalten werden:
Die Stärke des Zusammenhangs zwischen der tatsächlichen Beteiligung und der gewünschten Beteiligung ist auch status-unabhängig noch relativ hoch (R-Quadrat = 0.30 gegenüber ursprünglich 0,476).
Die partielle Regressionskonstante ist nur rechnerisch knapp kleiner "Null". In der Grafik geht die Funktion faktisch durch den Nullpunkt.
Der einfache partielle Regressionskoeffizient liegt mit 0,595 etwas unter dem einfachen Regressionskoeffizienten von 0,67.
Festzuhalten ist ausserdem, dass die Streuung der Beobachtungen um die Regressionsgerade noch beträchtlich ist, so dass weiterer Erklärungsbedarf bezüglich der Genese der Beteiligungswünsche besteht.
b) Die ein- und mehrfache partielle Korrelationsanalyse mit dem Tool "Korrelation"
Die einfache partielle Korrelation
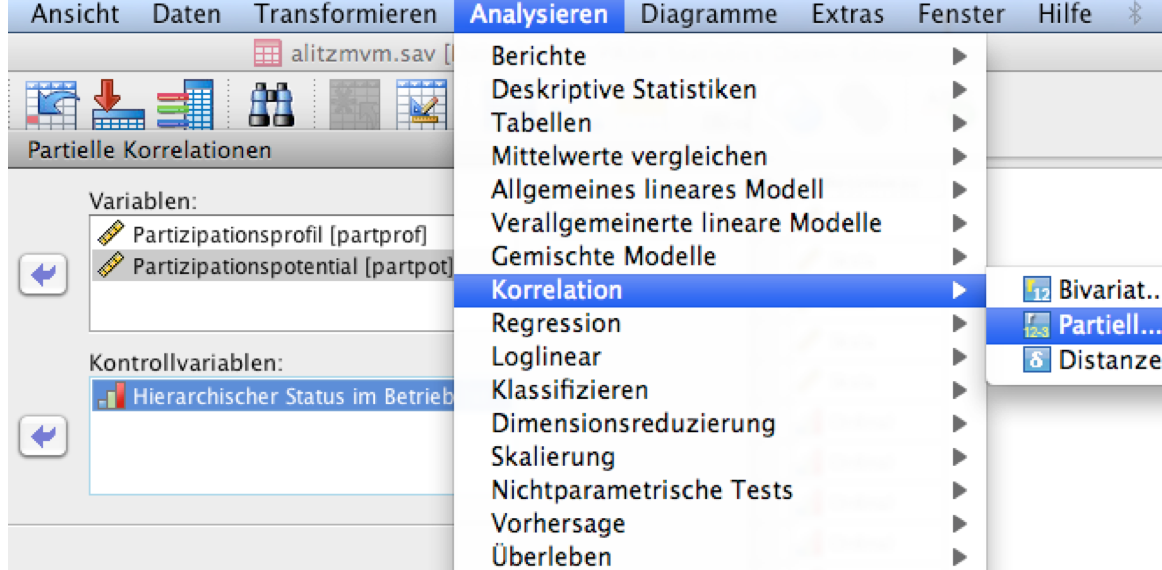
Dazu wird die Prozedur "Korrelation"aufgerufen und die Option "Partiell.."gewählt (vgl. Screenshot 12-23). Die Ergebnisse für die einfachen partiellen Korrelationen sind durch separate Eingaben der jeweiligen Kontrollvariablen "Status" bzw. "Alter" bzw. "Geschlecht" zu erzeugen.
Die separat berechneten Ergebnisse sind in der Tab. 12-2 festgehalten.
|
Screenshot 12-23: Die einfache partielle Korrelation mit SPSS
|
|
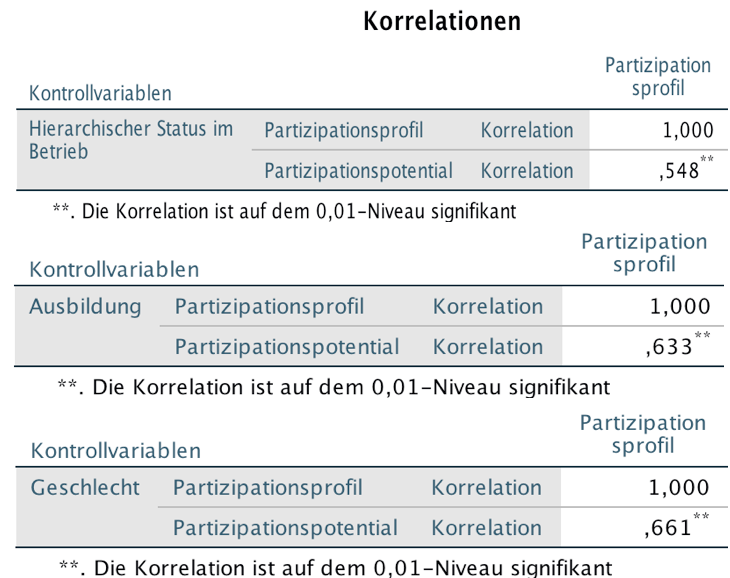
Tabelle 12-2: Ergebnisse zur einfachen partiellen Korrelation
|
|
|
Vergleicht man die verschiedenen einfachen partiellen Korrelationskoeffizienten mit dem nicht-partiellen Koeffizienten r = 0,69, so zeigt sich, dass eine Kontrolle der Status-Variablen mit 0,548 den größten Effekt aufweist. Am geringsten beeinträchtigt das Geschlecht den ursprünglichen Zusammenhang. Bei konstantem Ausbildungsniveau korrelieren die Beteiligungsvariablen immerhin noch mit einem r von 0,633.
Die mehrfache partielle Korrelation
Im Folgenden wird eine dreifach partielle Korrelation berechnet, bei der die drei Variablen "Status", "Ausbildung" und "Geschlecht" gemeinsam kontrolliert werden.
Diese werden in das SPSS-Eingabe-Fenster (vgl. Screenshot 12-23) in der Rubrik "Kontrollvariablen" gemeinsam eingetragen. Das Ergebnis ist im Screenshot 12-24 notiert:
Screenshot 12-24: Die mehrfache partielle Korrelation

Das Ergebnis weicht mit einem r von 0,528 kaum vom einfachen partiellen Korrelationskoeffizient mit kontrolliertem Status von 0,548 ab. Dies zeigt einerseits, dass die Kontrollvariablen unter einander hoch korreliert sind, andererseits dass die autonome Korrelation der Ausgangsvariablen stabil hoch ist.
Anmerkung: Eine Darstellung und Interpretation der induktiven Aspekte der partiellen Regressios- und Korrelationsanalyse findet sich in
ViLeS 2, Modul "Test der Regressions- und Korrelationskoeffizienten, Teil B" sowie unter
ViLeS 2, Modul "Konfidenzintervalle in der Regressions- und Korrelationsanalyse, Teil B" .
2. Aufgaben
a) Die Ausgangsdaten
Analysieren Sie unter Verwendung der Datei Wohnen.sav mit SPSS den einfachen linearen Regressions- und Korrelationszusammenhang zwischen den Variablen Miethöhe und Anzahl der Räume, sowie den einfachen partiellen Regressions- und Korrelationszusammenhang zwischen diesen Variablen unter Konstanthaltung der Wohnfläche.
b) Die Aufgabenstellung
Berechnen Sie dazu die Residuen beider Variablen aus ihren Beziehungen zur Variable Wohnfläche nach dem in Screenshot 12-21 demonstrierten Verfahren und stellen Sie den Zusammenhang zwischen den Residuen graphisch und rechnerisch analog zum Screenshot 12-22 dar. Interpretieren Sie die Ergebnisse.
Vergleichen Sie die, in den beiden Rechnungen ermittelten Regressions- und Korrelationskoeffizienten und finden Sie eine plausible Erklärung für die Umkehrung des positiven Zusammenhangs zwischen Miethöhe und Anzahl der Räume in einen negativen, sobald die Wohnfläche konstant gehalten wird.
|



