1. Vorbemerkungen

a) Multiple Interdependenzen im Datensatz

• Die bisher betrachteten zweidimensionalen Regressions- und Korrelationsmodelle analysieren in der Regel einen Ausschnitt des Beziehungsgeflechtes zwischen vielen Variablen.

• Betrachten wir dazu wieder die Beteiligungen an betrieblichen Entscheidungsprozessen, so spielen dabei nicht nur die tatsächliche und die gewünschte Beteiligung eine Rolle, sondern auch der hierarchische Status, das Ausbildungsniveau und möglicherweise auch das Geschlecht der beteiligten Personen eine Rolle.

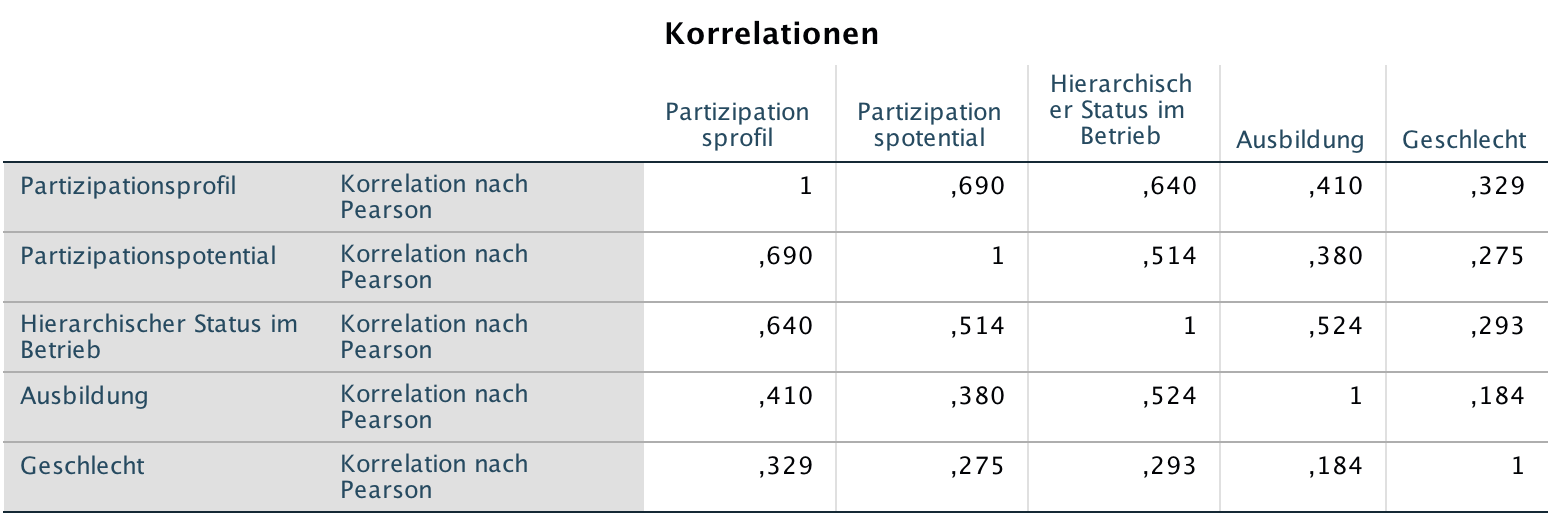
• Die Beziehungen zwischen diesen Variablen lassen sich in der nachstehenden Korrelationsmatrix darstellen:

  Tabelle 12-1 : Die Korrelationsmatrix der entscheidungsrelevanten Variablen
  

• Die Korrelationsmatrix belegt mehr oder minder starke Korrelationen zwischen allen Variablen. Zwar ist mit r = 0,69 die Korrelation zwischen der tatsächlichen Beteiligung (partprof) und der gewünschten Beteiligung (partpot) am grössten, doch auch die Zusammenhänge zwischen partprof und dem Status (r = 0,64), der Ausbildung (r = 0,41) und auch dem Geschlecht (r = 0,329) sind gewichtig.

b) Multiple Interdependenzen in Regressions- und Korrelationsmodellen

• In der Regressionsfunktion x₁ = a + b · x₂ + e werden die Wirkungen der Variablen
  x₂.... x_k zwar nicht völlig ausgeblendet, aber der Fehlervariablen e subsumiert und damit im Einzelnen nicht mehr erfassbar.

• Die Wirkungen weiterer Variablen lassen sich nun auf zwei verschiedene Weisen modellieren:

  • Das partielle Regressions- und Korrelationsmodell :

    Mit diesem Ansatz kann der Frage nachgegangen werden, ob ein bestimmter Zusammenhang durch weitere Variablen beeinträchtigt wird. Z.B. also, ob der Zusammenhang zwischen der gewünschten Beteiligung und der tatsächlichen Beteiligung durch den Status der Person mit determiniert oder gestört wird und wie stark er (noch) wäre, wenn dieser Einfluss ausgeschaltet würde. Daraus resultiert die:
    
    Dieses Modell wird in diesem Kapitel vorgestellt

  • Das multiple Regressions- und Korrelationsmodell :

    Im multiplen Regressions- und Korrelationsmodell lassen sich Erklärungs-Zusammenhänge durch weitere Variablen verdichten. Indem untersucht wird, ob die tatsächliche Beteiligung nicht nur durch den Status der Person, sondern auch durch deren Ausbildungsniveau, deren Geschlecht und letztlich auch durch deren Interesse an einer Beteiligung determiniert wird und dadurch insgesamt besser erklärt werden kann. Daraus ergibt sich die:
    
    

    Die Behandlung diese Modells erfolgt dann im nächsten Kapitel XII-6.

2. Das partielle Regressions- und Korrelationsmodell

a) Die Beeinträchtigung der Beziehung x₁ = f(x₂) durch weitere Variablen

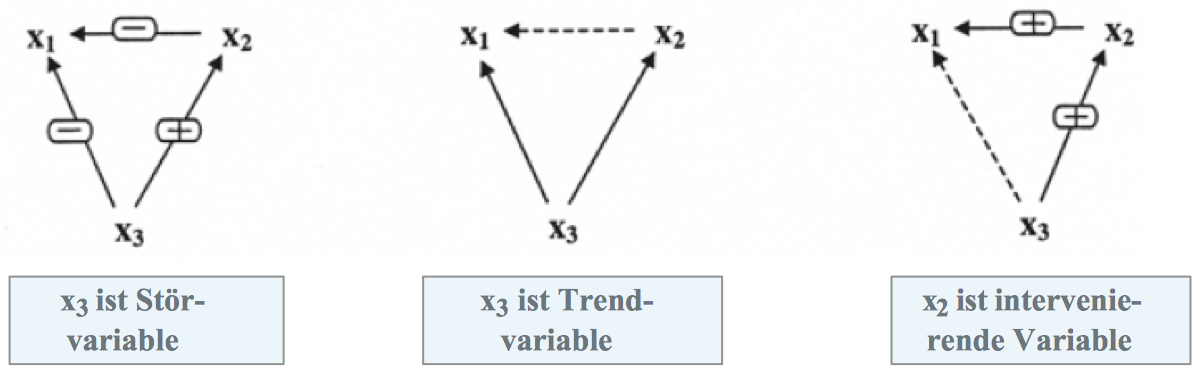
• Bei der Analyse einer Regressionsbeziehung soll das Resultat möglichst unbeeinflusst von weiteren Variablen ermittelt werden. Dabei sind drei verschiedene Typen von Einflüssen bedeutsam:
  

  • Die Störvariable:

    Ein Einfluss von Störvariablen liegt dann vor, wenn eine Variable x₃ entweder mit beiden Variablen gleichsinnig oder mit der einen Variablen positiv und mit der anderen Variablen negativ korreliert ist. Erst wenn diese Variable ausgeschaltet (konstant gehalten) wird, kann der eigentliche Zusammenhang zwischen x₁ und x₂ exakt ermittelt werden.

  • Die Trendvariable:

    Dies ist der Fall einer regionalen Korrelation von Storchennestern und Säuglingsgeburten, deren Anzahl aufgrund einer regionalen Industrialisierung gleichzeitig zurückgehen. Zwischen den Variablen besteht also nur eine Scheinkorrelation. Wenn die Trendvariable ausgeschaltet wird, ist keine Korrelation von mehr festzustellen.

  • Die intervenierende Variable:

    In diesem Fall sind die Wirkungen der Variablen funktional miteinander verknüpft. Wenn x₃ unverändert beleibt, ist auch keine Wirkung von x₂ zu verzeichnen.

• Abbildung 12-10: Mögliche Wirkungen einer Variablen x₃
     

b) Das Konzept der partiellen Regression und Korrelation

• Die Definition der Partialvariablen: Eine Partialvariable ist eine Variable x_j, aus der der Einfluss einer (oder mehrerer) Variablen ausgeschaltet wurde.

• Die Definition des partiellen Regressions-und Korrelationsmodells: Die partielle Regression und Korrelation ist eine einfache Regression und Korrelation von Partialvariablen. Es gelten dafür die bekannten Formeln für a und b und den Korrelationskoeffizienten analog für die Partialvariablen.

c) Die Varianten des partiellen Regressions- und Korrelationsmodells

• Das einfache lineare Partialmodell
  

  • Im einfachen linearen Partialmodell wird der Einfluss einer Variablen x₃ auf die Funktion x₁ = f(x₂) ausgeschaltet.

  • Der Status z.B. wirkt auf die tatsächliche Beteiligung (Partprof) und auf die gewünschte Beteiligung (Partpot). Sein Einfluss auf beide Variablen soll ausgeschaltet werden, um zu zu ermitteln, ob und wie Partprof und Partpot zusammenhängen, wenn der Status konstant gehalten wird.

  • Abbildung 12-11: Wirkungen einer Variablen x₃
    

    

• Das mehrfache lineare Partialmodell

  • Im mehrfachen linearen Partialmodell wird der Einfluss einer Reihe von Variablen x₃ ..... x_k auf die Funktion x₁ = f(x₂) ausgeschaltet.

  • Für eine unbeeinflusste Analyse von partpot = f (partprof) müssen die Einflüsse von Geschlecht, Ausbildung und Status der Reihe nach ausgeschaltet werden.

  • Abbildung 12-12: Wirkungen einer Reihe von Variablen
    

    

• Das semipartielle Modell
  

  • Im semipartiellen linearen Modell wird der Einfluss einer oder mehrerer Reihe Variablen nur aus der unabhängigen Variablen x₂ ausgeschaltet.

  • Abbildung 12-13: Wirkungen von x₃ auf x₂
    

    

  • Die semipartielle Analyse ist Teil der schrittweisen multiplen Analyse bei der die einzuschließenden, unabhängigen Variablen der Reihe um die Einflüsse der bereits einbezogenen unabhängigen Variablen bereinigt werden (vgl. dazu Kap. 12-6).

3. Das einfache partielle Regressions-und Korrelationsmodell

a) Die Beziehung zwischen den Partialvariablen x_1-3 und x_2-3

• Die Definition der Partialvariablen x_1-3 und x_2-3:

  Die Partialvariablen x_1-3 und x_2-3 sind der Teil der Ausgangsvariablen, der sich ergibt wenn der Einfluss von x₃ ausgeschaltet wurde. Damit wird der Zusammenhang x₁ = f(x₂) unter der Bedingung analysiert, dass x₃ konstant gehalten wird:
  

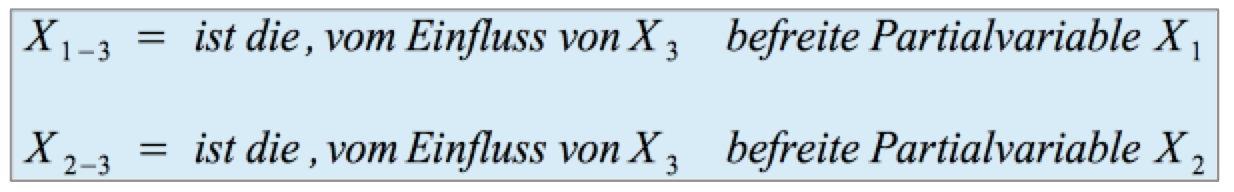
• Das einfache partielle Regressionsmodell:
  

b) Die Auspartialisierung des Einflusses von x₃

• Ausgangspunkt: Die Fehlervariable:

  Abbildung 12-14: Die Fehlervariable e_i als Partialvariable
  

  

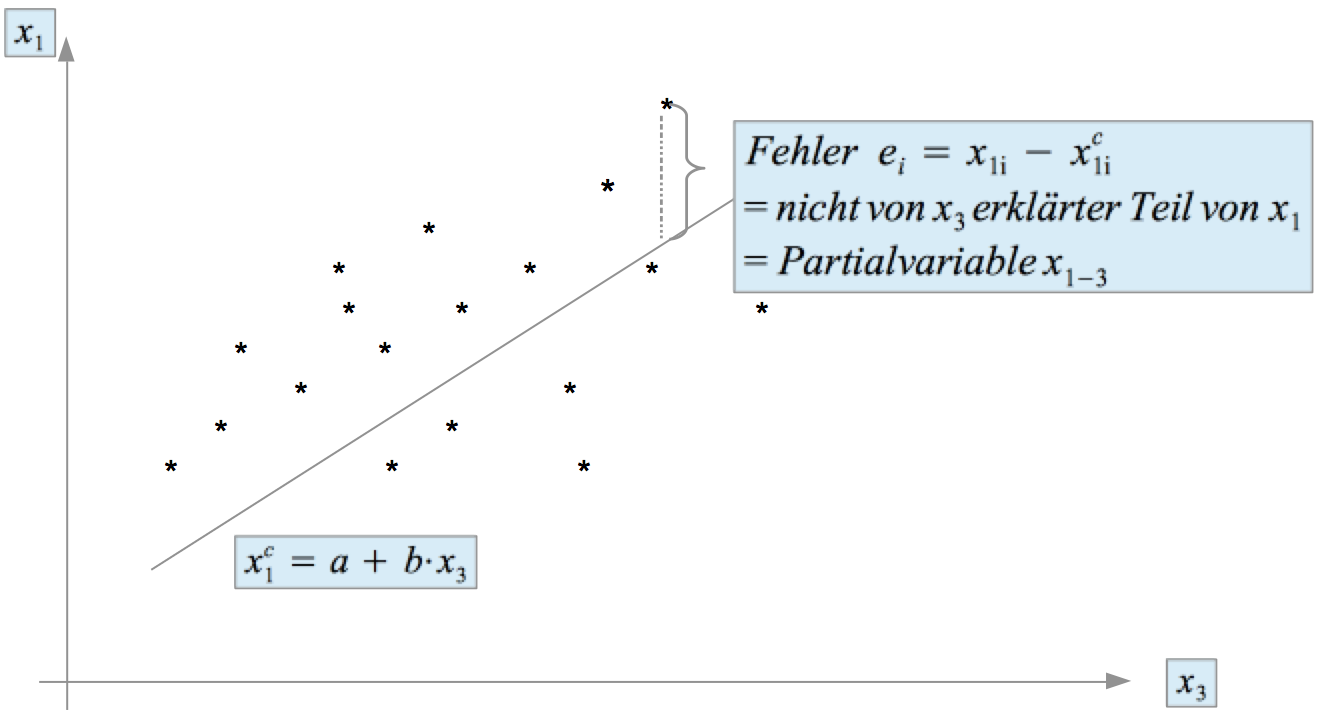
• Die Konstruktion der Partialvariablen:

  Abbildung 12-15: Drei Schritte zur Partialfunktion
  

  

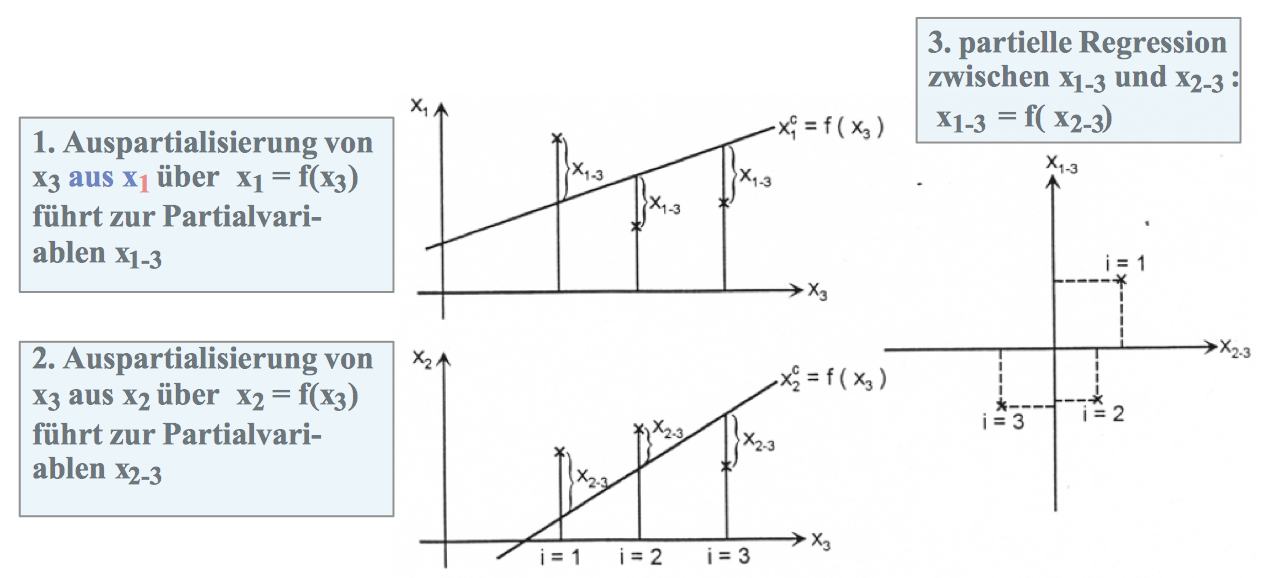
c) Die Komponenten des einfachen partiellen Regressions- und Korrelationsmodells

• Die Eigenschaften der Partialvariablen:

  Die Partialvariablen besitzen:

  • Mittelwerte von Null:
    und

  • Varianzen von:
    

• Die Regressionsparameter

  • Die Regressionskonstante:
    

  • Der Regressionskoeffizient:
    

  • Der Korrelationskoeffizient
    

4. Die mehrfache partielle Regressions- und Korrelation

a) Die Ausgangskonstellation

• Die Strukturprinzipien des mehrfachen Partialmodells werden hier am Beispiel einer dreifachen Partialanalyse entwickelt.

• Abbildung 12-16: Wirkungen von x₃ und x₄ auf x₁ = f( x₂)
  

  

b) Die Partialvariablen

Die beiden auszupartialisierenden Variablen x₃ und x₄ werden nacheinander ausgeschlossen. D.h. im ersten Schritt wird die Variable aus den Variablen eliminiert. Damit erhalten wir zuerst die Partialvariablen 2. Ordnung und danach die 3. Ordnung:

• Die Partialvariablen 2. Ordnung:
  

  Wichtig dabei ist, dass der Einfluss der Variablen x₃ nicht nur aus x₁ und aus x₂ sondern auch aus x₄ eliminiert werden muss.

• Die Partialvariablen 3. Ordnung::
  

c) Die Regressionsfunktion

• Die Funktionsform:
  

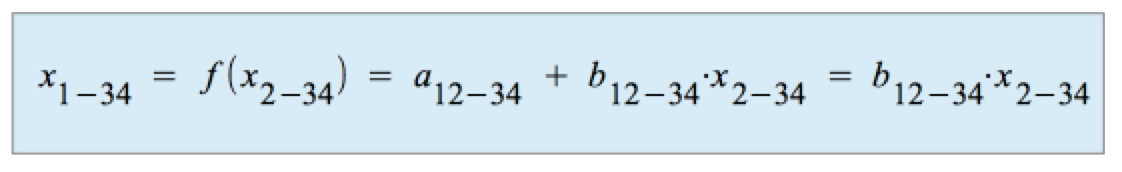
• Die dreifache partielle Regressionskonstante :
  

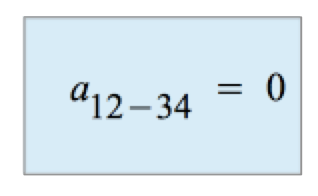
• Der dreifache partielle Regressionskoeffizient :
  

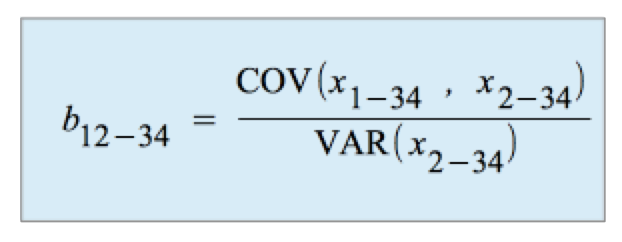
  Anmerkung: Analog zum einfachen partiellen Regressionskoeffizienten gehen in den mehrfachen partiellen Regressionskoeffizienten ebenfalls alle einfachen Korrelationskoeffizienten des Modells (r₁₂ .....r₃₄) in die entwickelte Formel ein (zur Formel und zur Ableitung vgl. Litz: Multivariate Statistische Methoden, München 2000)

d) Der Korrelationskoeffizient

• Die partiellen Korrelationskoeffizienten basieren auf den einfachen Korrelatonskoeffizienten der Korrelationsmatrix. Für den Koeffizienten r_12-34 ergibt sich so:
  

5. Die semi-partielle Regressions- und Korrelation

a) Die Ausgangskonstellation

• Bei der semipartiellen Korrelation wird die Störvariable nur aus der unabhängigen Variablen auspartialisiert. Dies soll hier am Beispiel der einfachen semi-partiellen Regression und Korrelation demonstriert werden.

• Betrachtet wird die Funktion x₁ = f( x_2-3) mit der Partialvariable 1. Ordnung x_2-3.

b) Die Komponenten des Modells

• Die Regressionsfunktion:

  mit der Funktionsform:
  

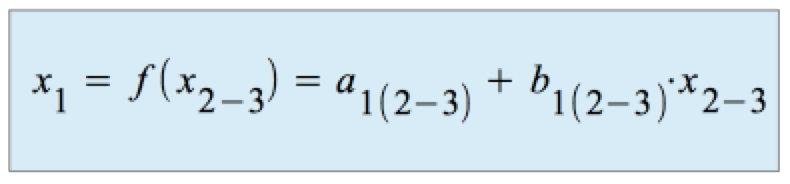
• Die einfache semi-partielle Regressionskonstante :
  

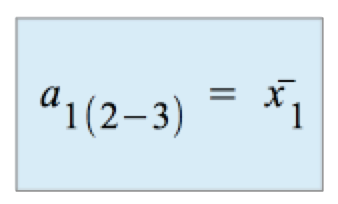
  Damit entspricht die einfache semi-partielle Regressionskonstante dem arithmetischen Mittel der abhängigen Variablen.

• Der einfache semi-partielle Regressionskoeffizient :
  

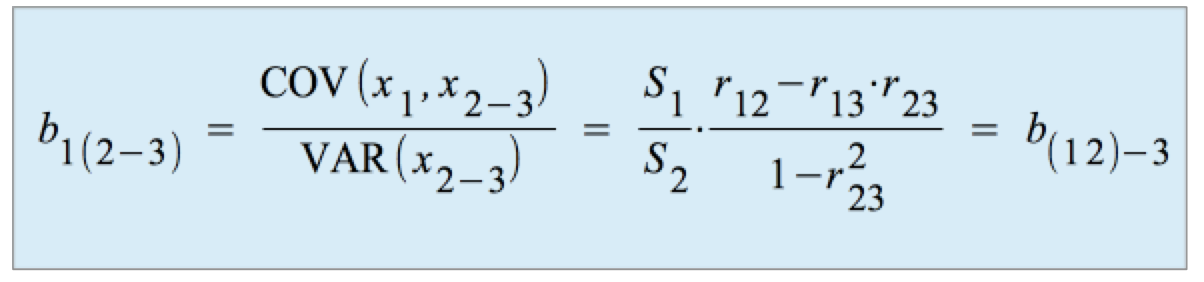
  Damit entspricht der einfache semi-partielle Regressionskoeffizient dem einfachen partiellen Regressionskoeffizienten

c) Der einfache semi-partielle Korrelationskoeffizient

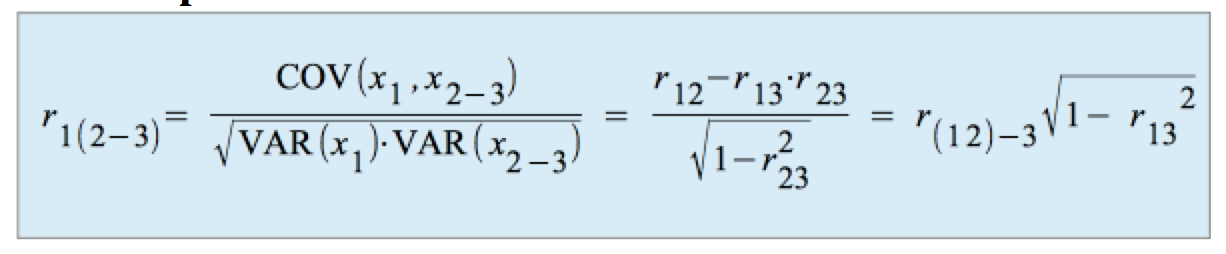
Damit ist der einfache semi-partielle Korrelationskoeffizient um den Betrag 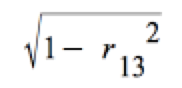kleiner als der einfache partielle Korrelationskoeffizient.

---

Hinweis zur Navigation, zum Ausdrucken und zur Bewertung: In der Abschusszeile finden Sie einen Link zur Druckversion, zum vorherigen und zum nächsten Arbeitsschritt und mit der Sitemap eine Übersicht über das gesamte Angebot. Zur Bewertung: Diese Seite ist überarbeitet worden. Deshalb wurden die bisherigen Bewertungen gelöscht. Bewerten Sie bitte diese aktualisierte Seite neu und helfen Sie uns, damit dieses Angebot weiter zu verbessern: Diese Seite ist: sehr gut    gut    eher gut    mittelmäßig    eher schlecht    schlecht    sehr schlecht Diese Seite wurde von 1 Benutzer mit "sehr gut" bewertet.

1/2 50 % Fortschritt

 

| Feedback | Copyright | Übersicht | Druckversion | Log-Out | Sitemap | Nächster Arbeitsschritt |