 |
Nichtlineare Kurvenanpassungen mit SPSS - Beispiele und Aufgaben im Modul XII-3 Das nichtlineare Regressions- und Korrelationsmodell
Vorbemerkung
Nachstehend wird am Beispiel der Datei Partizipation_1.sav und den dort enthaltenen Variablen Partizipationsprofil und Status gezeigt, wie mit SPSS nicht-lineare Regressions- und Korrelationsanalysen graphisch veranschaulicht und rechnerisch durchgeführt werden und wie die Ergebnisse im Hinblick auf Richtung und Stärke des Zusammenhangs der Variablen zu interpretieren sind.
Danach wird die Vielzahl von Möglichkeiten vorgestellt, die SPSS mit der Programmkomponente "Regression -> Kurvenanpassung" zur Analyse nichtlinearer Regressionsbeziehungen bereithält.
Schließlich werden dazu Aufgaben zum Arbeiten mit dem SPSS-Tool "Kurvenanpassung" und Daten aus dem Bereich Wohnen gestellt.
1. Die nichtlineare Regressions zwischen der Variable Partizipationsprofil und der Variable Status
Diese Analyse greift auf das grafische Beispiel zur quadratischen Regression zurück, das im vorangegangenen Abschnitt in Abb. 12-4 vorgestellt wurde.
Dieser Grafik lag die Frage zugrunde, wie weit der betriebliche Status die Beteiligung an betrieblichen Entscheidungsprozessen bestimmt und ob dieser Zusammenhang nicht-linearen Charakter hat. Dabei sei vorläufig unterstellt, dass die Statuspositionen äquidistant sind.
Im Folgenden werden zuerst die Analysen an Hand von Streudiagrammen mit dem Analysetool "Diagramme" veranschaulicht und danach mit den Programmpaketen "Regression" rechnerisch durchgeführt und tabellarisch präsentiert.
a) Die graphische Regressionsanalyse mit SPSS
Der Aufruf zur Analyse erfolgt wieder über die Befehlskette: Grafik > alte Dialogfelder > Streu-/Punktdiagramm > einfaches Streudiagramm und wird mit der Eingabe der Variablen abgeschlossen.
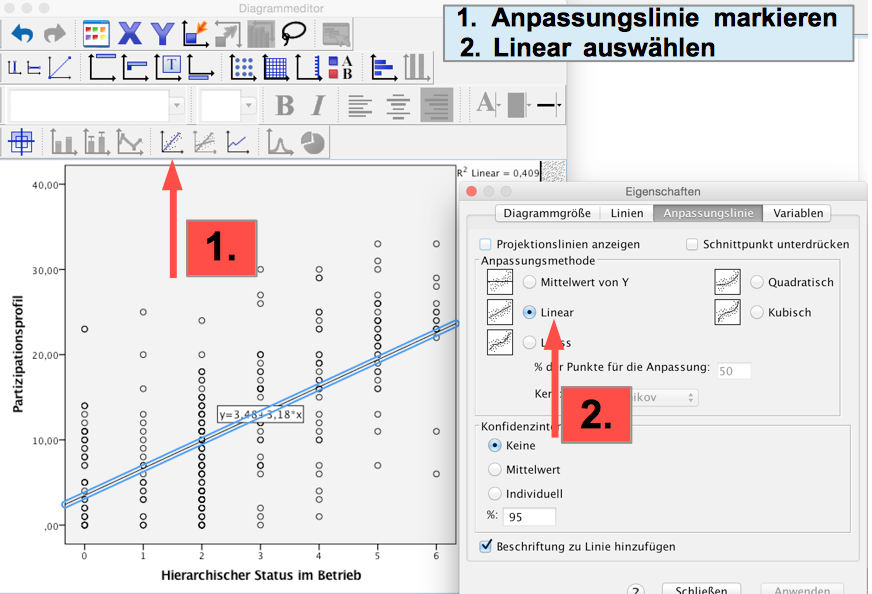
Nach einem Doppelklick auf die Grafik wird im Diagramm-Editor zuerst eine lineare (vgl. Screenshot 12-11), dann die quadratische Anpassungslinie (vgl. Screenshot 12-12) ausgewählt:
|
Screenshot 12-11: Streuungsdiagramm mit linearer Anpassungslinie anforden
|
|
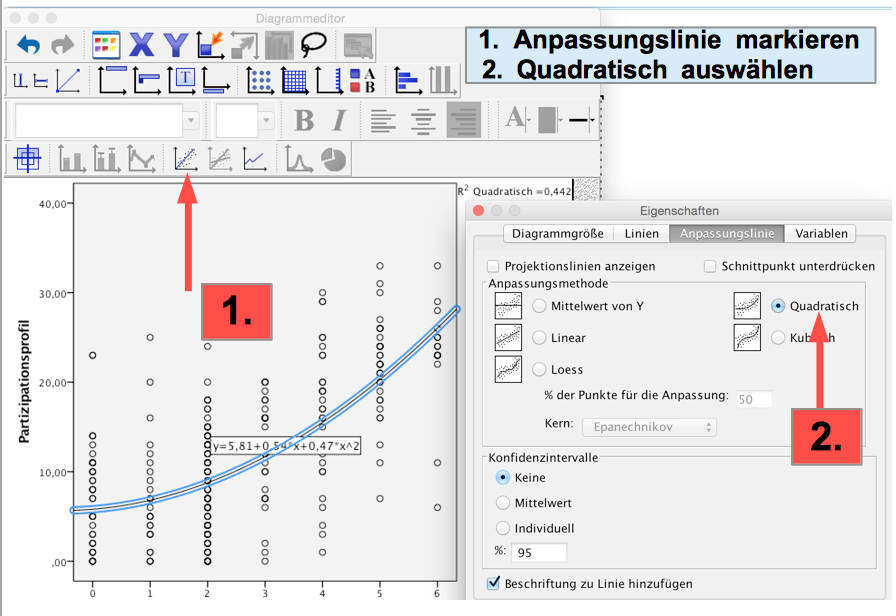
Screenshot 12-12: Streuungsdiagramm mit quadratischer Anpassungslinie anfordern
|
|
|
Für die lineare Regressions- und Korrelationsanalyse ist als Ergebnis eine Regressionsfunktion y = 3,48 + 3,18 x und ein R-Quadrat von 0,409 eingeblendet.
Für die quadratische Regressions- und Korrelationsanalyse ergibt sich eine Regressionsfunktion y = 5,81 + 0,54 x + 0,47 x 2 und ein R-Quadrat von 0,442 (zur Interpretation vgl. nachstehend Punkt d).
b) Die Kurvenanpassung mit SPSS anfordern
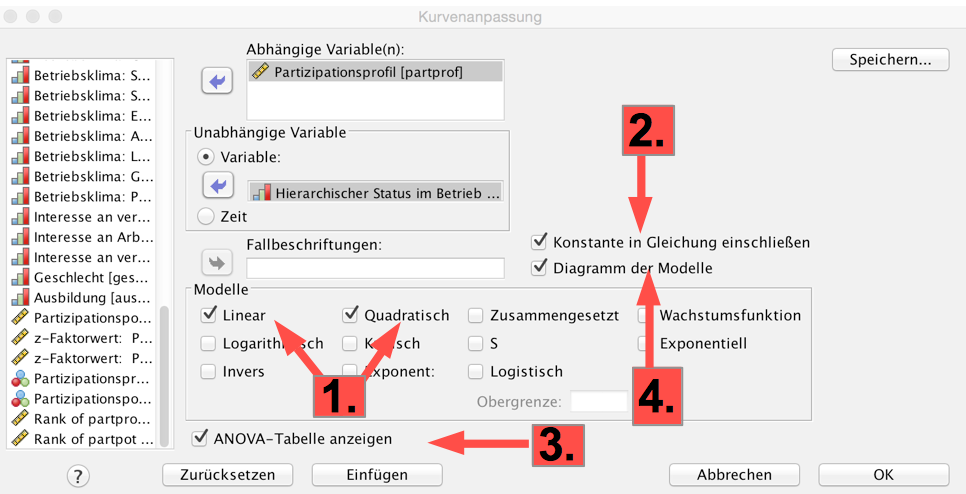
Die nicht-lineare Regressions und Korrelationsanalyse wird in SPSS als "Kurvenanpassung" bezeichnet. Dazu wird die Programmkomponente "Analysieren > Regression" aufgerufen und darunter die Prozedur "Kurvenanpassung".
Screenshot 12-13: Kurvenanpassung mit SPSS anfordern
|
|
Erläuterungen:

|
|
|
c) Die Ergebnisse der Kurvenanpassung
|
|
|
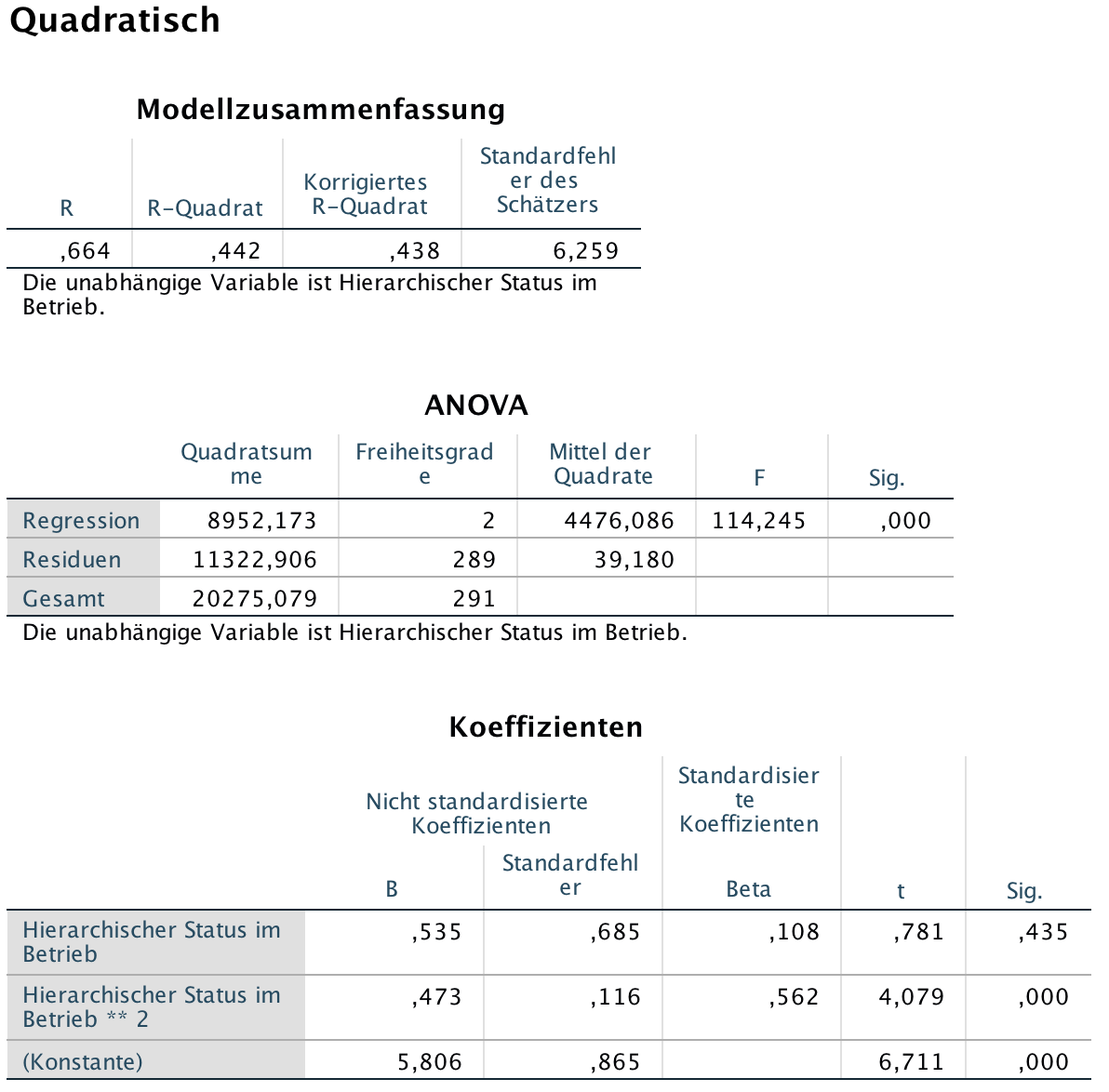
Screenshot 12-15: Die Ergebnisse der quadratischen Kurvenanpassung
|
|
|
Für die lineare Regressions- und Korrelationsanalyse erhalten wir eine Regressionskonstante von 3,48 und einen Regressionskoeffizienten von 3,18, sowie ein R-Quadrat von 0,409.
Für die quadratische Regressions- und Korrelationsanalyse ergibt sich eine Regressionsfunktion y = 5,81 + 0,54 x + 0,47 x 2 und ein R-Quadrat von 0,442.
Das angeforderte Diagramm entspricht den in den Screenshots 12-11 und 12-12 präsentierten Abbildern.
d) Die Interpretation der Ergebnisse
Im Vergleich der Modelle ist augenscheinlich, dass das quadratische Regressionsmodell etwa 4% der Varianz der Partizipation mehr erklärt als die lineare Analyse. Aus diesem Grund erscheint es vordergründig als das Modell der Wahl.
Andererseits ist nach der theoretischen Legitimation dieses Modells zu fragen, die vor allem für die Interpretation der Regressionsfunktion und hier besonders für die des Koeffizienten b2 relevant ist. b2 gibt an um welches Ausmaß y steigt, wenn x22 um eine Einheit zunimmt. Ein m2 bezeichnet eine Fläche, was ist aber real eine Statusposition2 und was bedeutet es, wenn diese Größe um eine Einheit zunimmt?
Im Falle dieses Beispiels ist zu konstatieren, dass die Aussagekraft des linearen Modells verbesserungsfähig ist, dass allerdings eine quadratische Regressionsanalyse kein tauglicher Weg ist.
Im Kontext nichtlinearer metrischer Modelle hatte das Beispiel also vor allem die Funktion, auf einfache Weise in die formalen Konzepte einzuführen und auch auf eine unsachgemäße, rein formale Behandlung dieser Modelle hinzuweisen.
Das statistische Problem liegt hier in der, der Variablen Status unterstellten Metrik. Dieses lässt sich allerdings in den nächsten Abschnitten mit dem Modell der einfaktoriellen Varianzanalyse (für ordinal-skalierte unabhängige Variablen) beheben.
2. Beispielsrechnungen für die Gesamtheit der nichtlinearen Regressionsanalysen mit SPSS
a) Vorbemerkungen
Das SPSS-Programm "Kurvenanpassungen" offeriert insgesamt zehn verschiedene Funktionstypen für nichtlineare Regressions- und Korrelationsanalysen. Diese sollen nachstehend mathematisch formuliert und grafisch veranschaulicht werden.
Wir betrachten zuerst die in den Parametern lineare Funktionen (Typ I), deren Definitionsbereich auch negative Werte enthalten kann. Dazu beziehen wir uns beispielhaft auf die Ausgangsvariablen Partizipationsprofil und -potential sowie auf deren standardisierte Formen.
Danach werden die Funktionen präsentiert, deren Transformationen auf logarithmischer Grundlage erfolgen (Typ 2). Diese sind deshalb nur für positive Werte der abhängigen und/oder der unabhängigen Variable möglich. Die Ausprägung "0" der zur Analyse herangezogenen Variablen Partizipationsprofil und -potential wird dazu auf "0,5" rekodiert.
b) Kurvenanpassungen (Typ I)
Hier werden die quadratische, die kubische und die inverse Regression und Korrelation diskutiert und mit der linearen formal, rechnerisch und grafisch verglichen.
Die Funktionen und ihre Transformation:
Übersicht 12-2: Funktionen und Transformationen nicht-linearer Anpassungslinien (Typ I)

Der grafische Vergleich der Ergebnisse zu den Ausgangsvariablen:
Screenshot 12-16: Streuungsdiagramm und Funktionen (Typ I)
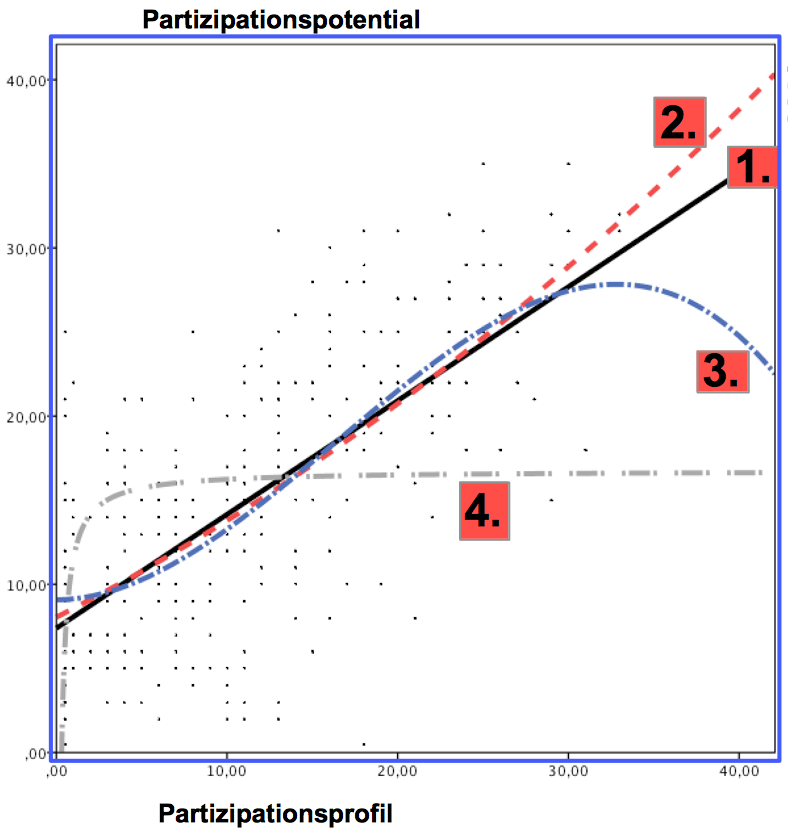

Der rechnerische Vergleich der Ergebnisse zu den Ausgangsvariablen:
Screenshot 12-17: Regressions- und Korrelationskoeffizienten zu den Kurvenanpassungen des Typs I

Der grafische Vergleich der Ergebnisse zu den standardisierten Variablen:
Screenshot 12-18: Streuungsdiagramm und Funktionen (Typ I) für standardisierte Variablen
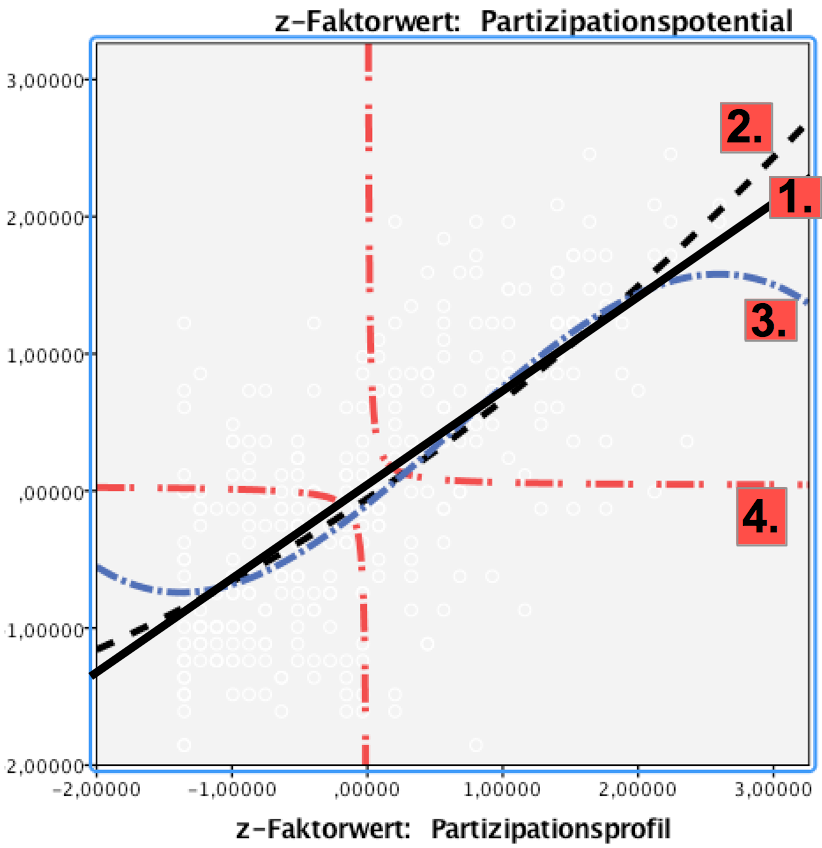

Der rechnerische Vergleich der Ergebnisse zu den standardisierten Variablen:
Screenshot 12-19: Regressions- und Korrelationskoeffizienten zu den Kurvenanpassungen des Typs I für standardisierte Variablen

Vergleich und Interpretation der Ergebnisse zu den Kurvenanpassungen des Typ I
Im Vergleich der Analysen der Ausgangsvariablen mit den Analysen der standardisierten Variablen unterscheiden sich die grafischen Verläufe wie die rechnerischen Ergebnisse zu R-Quadrat jeweils für die linearen, die quadratischen und die kubischen Regressionen nicht.
Deutliche Unterschiede ergeben sich für die inversen Regressionen: Hier erhalten wir bei den standardisierten Variablen aufgrund der negativen Werte zwei Äste. Dies führt zu Unterschieden in R-Quadrat und den Regressionsparametern. Allerdings erweisen sich die beiden inversen Modelle sowohl theoretisch wie empirisch als wenig geeignet, den Zusammenhang zwischen den Variablen adäquat zu modellieren.
Vergleicht man den linearen mit dem quadratischen und dem kubischen Ansatz, so zeigt sich eine leichte Verbesserung der Erklärungskraft um 0,3 bzw. um 0,6%. Im Fazit ist das kubische Modell dem linearen nicht nur wegen des größeren R-Quadrat sondern auch aus theoretischen Gründen vorzuziehen.
So ist es durchaus plausibel, dass eine Zunahme der Entscheidungsmöglichkeiten im unteren Bereich noch nicht zu einer deutlicheren Zunahme der Beteiligungswünsche führt und andererseits im oberen Kompetenzbereich "Sättigungstendenzen" auftreten können. Eine faktische Zunahme der Entscheidungskompetenzen generiert vor allem also im mittleren Bereich ein deutliche Zunahme der Beteiligungswünsche.
c) Kurvenanpassungen (Typ II)
Die Funktionen und ihre Transformation:
Übersicht 12-3: Funktionen und Transformationen nicht-linearer Anpassungslinien (Typ II)

Die Spezifikation der Modelle
Screenshot 12-20: nicht-lineare Anpassungslinien (Typ II) anforden
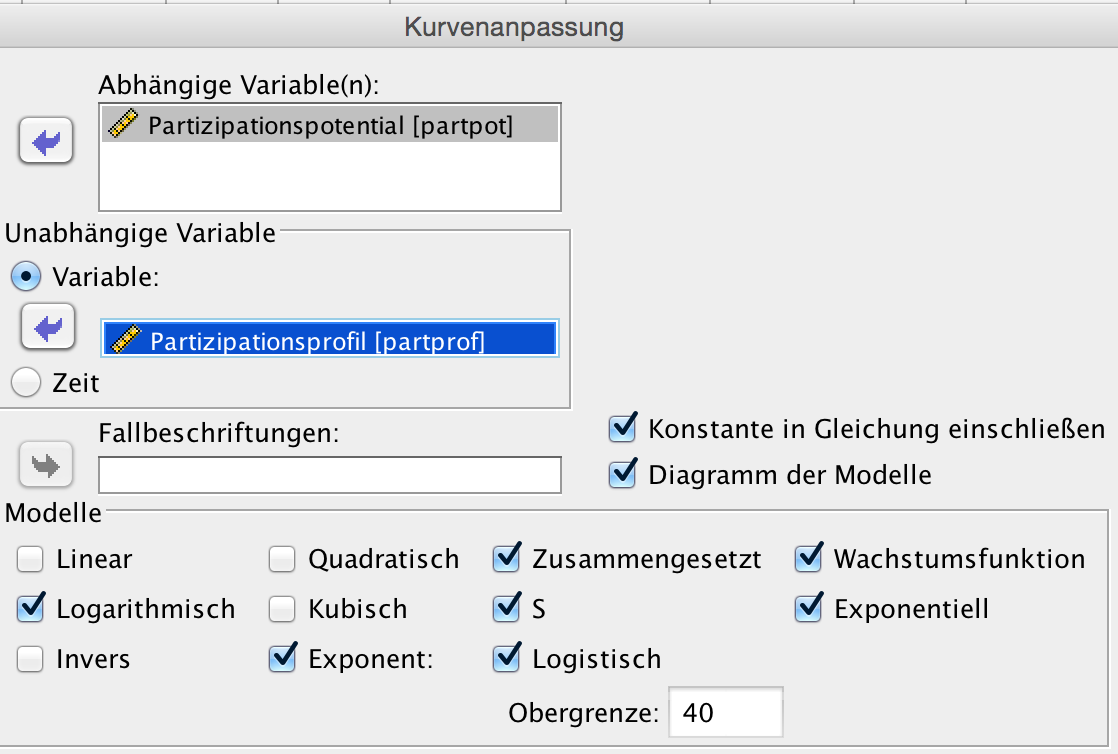
Hinweis: Für die abhängigen und/oder die unabhängigen Variablen sind nur positive Werte zulässig. Deshalb wurden die Ausprägung "0" der Variablen Partizipationsprofil und -potential auf "0,5" rekodiert.
Für das logistische Modell wurde als Obergrenze der abhängigen Variablen der Wert 40 eingegeben. Fehlt diese Eingabe wird das Modell nicht oder falsch berechnet.
Der grafische Vergleich der Ergebnisse zu den Ausgangsvariablen:
Screenshot 12-21: Streuungsdiagramm und nicht-lineare Anpassungslinien (Typ II)
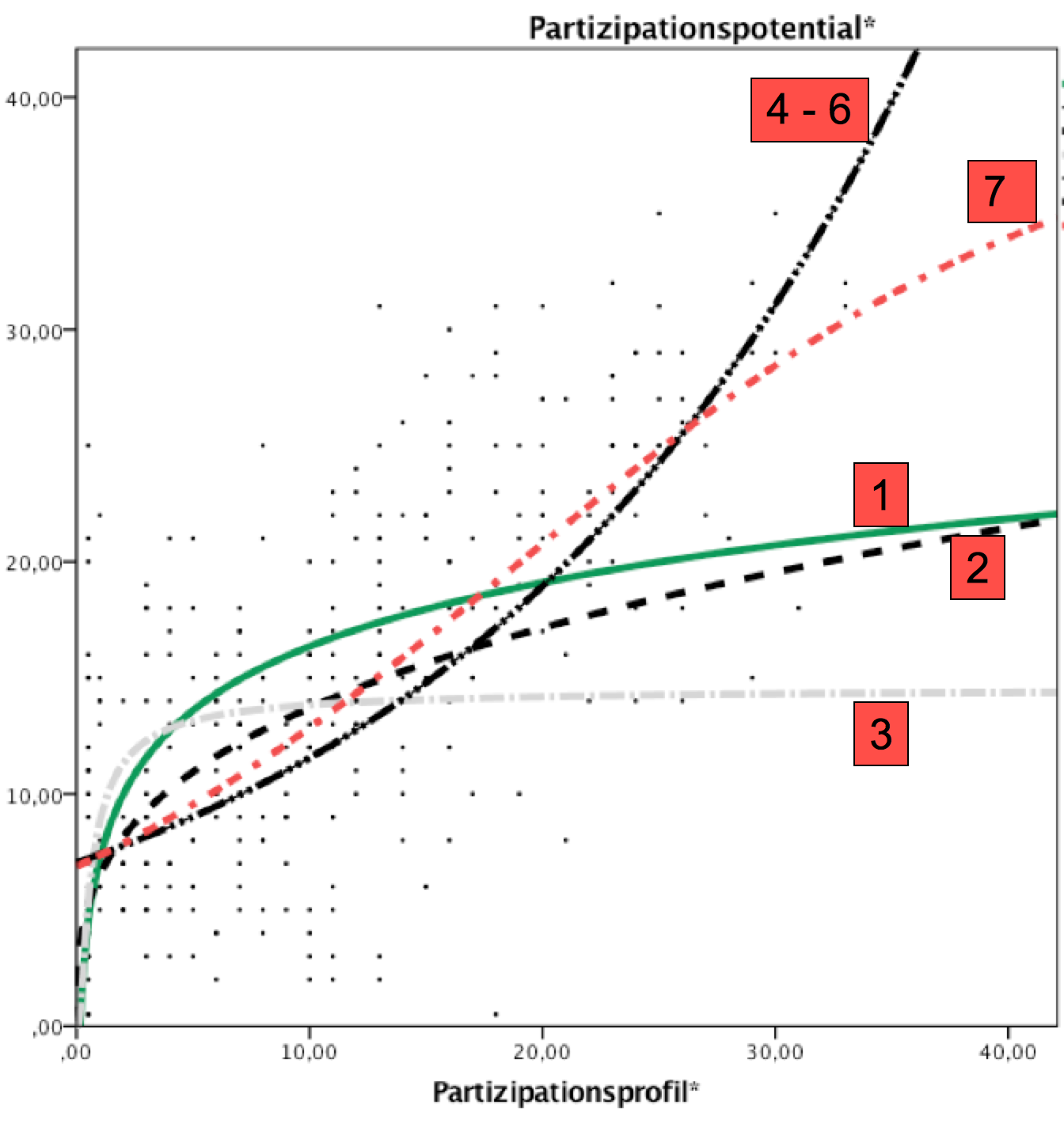

Der rechnerische Vergleich der Ergebnisse zu den Ausgangsvariablen:
Screenshot 12-22: Regressions- und Korrelationskoeffizienten zu den Kurvenanpassungen des Typs II
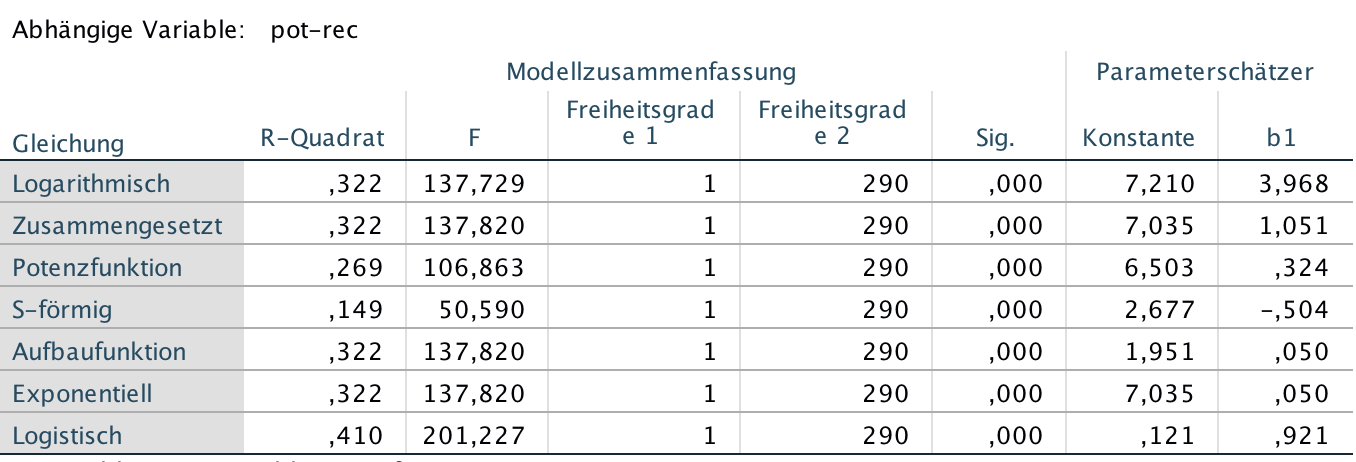
Vergleich und Interpretation der Ergebnisse zu den Kurvenanpassungen des Typ II
Unter den hier behandelten 7 verschiedenen Funktionsformen finden wir sowohl für die grafischen Verläufe wie für die rechnerischen Ergebnisse zu R-Quadrat eine Reihe von sehr ähnlichen Resultaten. Dabei unterscheiden sich die zusammengesetzte Funktion (4), die Aufbau- bzw. Wachstumsfunktion(5) sowie die exponentielle Funktion (6) sowohl in den Werten der Konstanten a wie im Regressionskoeffizienten b z.T. deutlich. Gleichwohl sind ihre Grafen identisch.
Deutliche Unterschiede ergeben sich zur logarithmischen und der logistischen wie der Potenz- und der S-Funktion, deren Grafen sich in einem unteren Wertebereich des Partizipationspotentials bewegen.
Bezüglich der Stärke der Zusammenhänge zeigt sich ein deutlicher Rückgang der Erklärungskraft der Modelle auf etwa 15 - 30%. Dies und das Fehlen plausibler theoretischer Erklärungen für die Verläufe verweist eher auf den Demonstrationscharakter dieser Analysen als auf ihre empirische Relevanz.
3. Aufgaben
a) Die Ausgangsdaten
Analysieren Sie unter Verwendung der Datei Wohnen.sav mit SPSS den linearen Zusammenhang und die nichtlinearen Zusammehänge zwischen den Variablen Wohnfläche, Miete und Haushaltseinkommen.
Betrachten Sie dazu die Variablenpaare Miete-Wohnfläche, Miete-Einkommen und Wohnfläche-Einkommen.
b) Die Aufgabenstellung
Führen Sie die Regressions- und Korrelationsanalyse für die Variablenpaare durch und interpretieren Sie die Ergebnisse für das lineare und das aussagefähigste nichtlineare Modell.
Vergleichen Sie dazu für diese Modelle die ermittelten Determinationskoeffizienten und formulieren Sie für die nichtlinearen Modelle eine Aussage über die möglichen theoretischen Gründe der Nichtlinearität.
|



