 |
Konzepte und Definitionen im Modul XII-3 Das nichtlineare Regressions- und Korrelationsmodell
1. Die Relevanz nichtlinearer Regressions- und Korrelationsmodelle
Die Linearität eines Zusammenhangs impliziert eine Proportionalität der abhängigen und unabhängigen Variablen und damit eine gleichgerichtete Veränderung beider.
Manche Sachverhalte decken sich nicht mit dieser Annahme: Entweder signalisiert die Gestalt der Punktwolke Nichtlinearität oder die theoretische Aussage über die Beziehung zwischen den beiden Variablen ist damit nicht kompatibel.
Nichtlineare Funktionen sind vor allem in den Wirtschaftswissenschaften bekannt. So basieren Produktionsfunktionen auf multiplikativen Verknüpfungen von Produktionsfaktoren, Konsumfunktionen unterstellen mit wachsendem Einkommen Sättigungstendenzen bei den Konsumenten und Wachstumsmodelle werden mit Exponentialgleichungen formuliert.
Da die Anzahl der möglichen mathematischen Funktionen fast beliebig ist, die Modelle oft sehr komplex und die Schätzverfahren damit sehr aufwändig, werden im folgenden nur einige mathematisch und statistisch einfache und besonders relevante
Ansätze beschrieben.
Im Modul "Beispiele und Aufgaben" wird dabei auch auf die verfügbaren Modelle im SPSS-Analysetool "Regression - Kurvenanpassung" eingegangen.
2. Modellansätze
a) Ein graphischer Vergleich eines linearen mit einem quadratischen Modell
Nachstehend sollen die grundlegenden konstruktiven Problem einer nichtlinearen Analyse an einem einfachen Modell veranschaulicht und Lösungsansätze im Hinblick auf die Ermittlung von Richtung und Stärke des Zusammenhangs der Variablen vorgestellt werden.
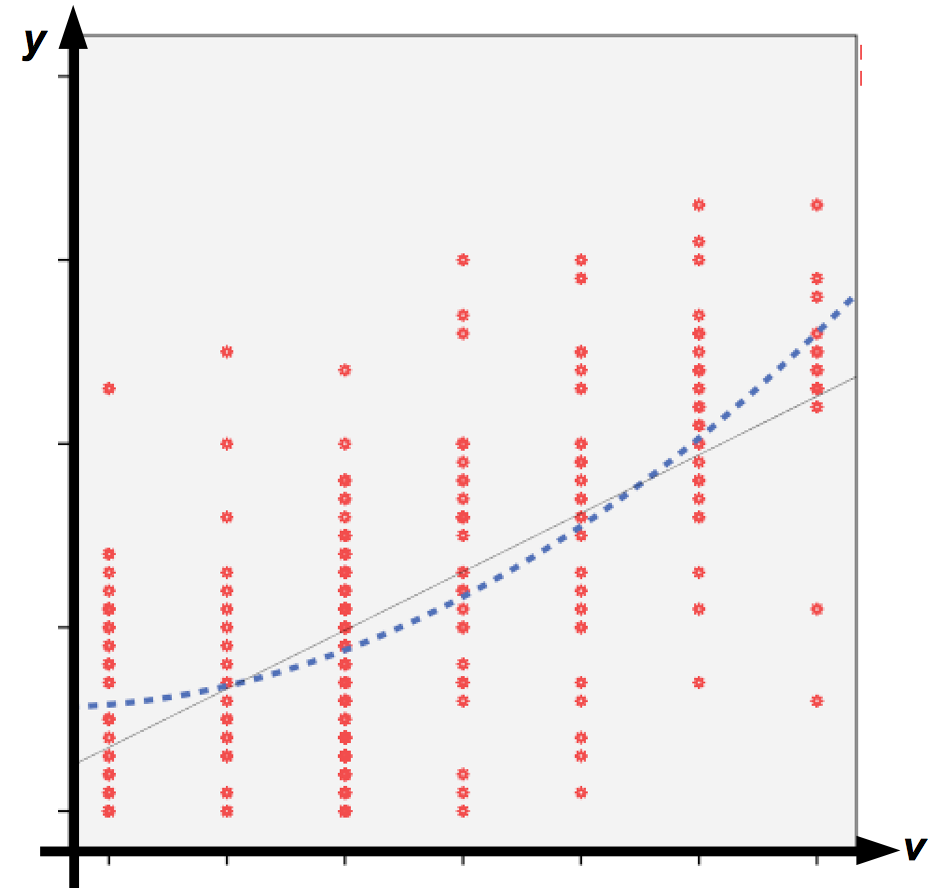
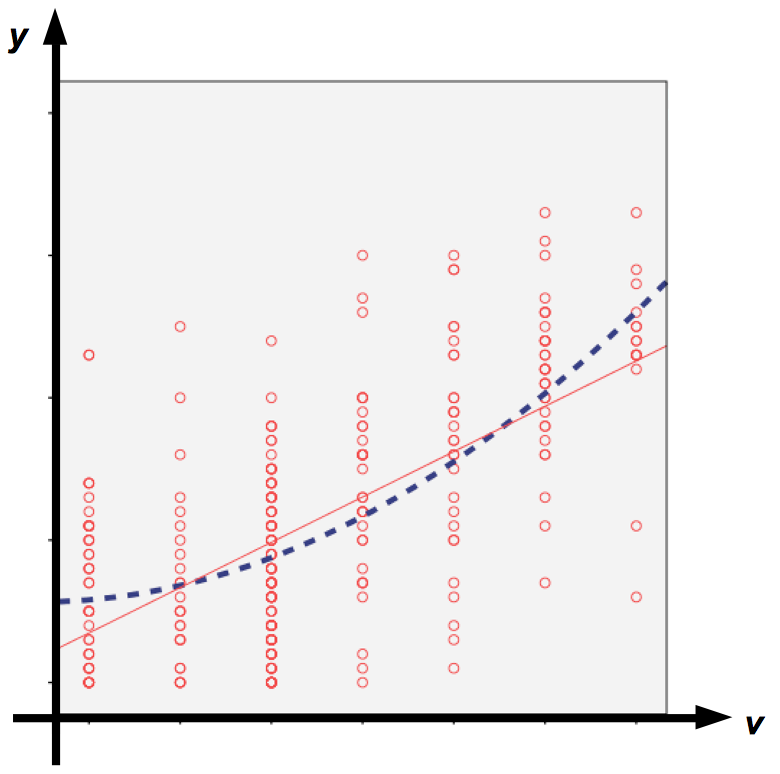
In Abb. 12-4 weist die Gestalt der Punktwolke auf einen möglicherweise nichtlinearen, progressiven Zusammenhang der beiden Variablen hin. Unter empirischen Aspekten wäre zu prüfen, ob ein nicht-linearer Verlauf der Kurve, beschrieben etwa mit einer quadratischen Funktion, bessere Ergebnisse, also höhere Werte in den Zusammenhangsmaßen liefert als die ebenfalls eingezeichnete lineare Funktion.
Zur Unterscheidung der Modelle werden in Folgenden je nach Modellformulierung die abhängigen Variablen mit y bzw. mit x1 und die unabhängigen Variablen mit v bzw. mit x2 bezeichnet.
Abbildung 12-4: Lineare und nichtlineare Regressionsfunktionen
b) Die Formulierung des quadratischen Modell
Dem quadratischen Modell können folgende Funktionsgleichungen zugrunde gelegt werden:
ein Modell, das nur die quadratische Komponente enthält:
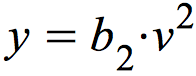
ein Modell, das neben der quadratischen Komponente eine Konstante einschließt:
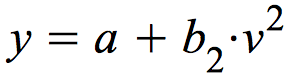
ein Modell, das neben der Konstanten, eine lineare und die quadratische Komponente enthält:
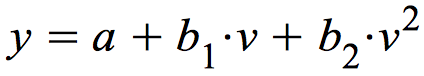
Die in Abb. 12-4 dargestellte quadratische Funktion entspricht dem vollständigen Modell mit den drei Komponenten. Dieses Modell wird unter "Beispiele und Aufgaben" ausführlich vorgestellt. Hier sei nur vermerkt, dass der Determinationskoeffizient vom linearen Modell mit einem R-Quadrat von 0,409 auf ein R-Quadrat im quadratischen Modell von 0,442 steigt. Dieses Modell gehört zu einer Klasse von Modellen, die in den Parametern lineare Funktionen aufweisen. Die Nichtlinearität ergibt sich über die Art des Einbezugs der unabhängigen Variablen, die Modellkomponenten selbst sind additiv mit einander verknüpft.
c) In den Parametern lineare Funktionen
In den folgenden Abbildungen betrachten wir neben dem quadratischen Modell, ein inverses Modell mit der unabhängigen Variablen v-1 und ein logarithmisches Modell mit der unabhängigen Variable ln(v) :
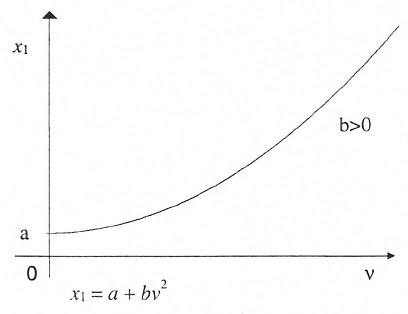
Abbildung 12-5: Quadratisches Modell mit einer Konstanten
|
|
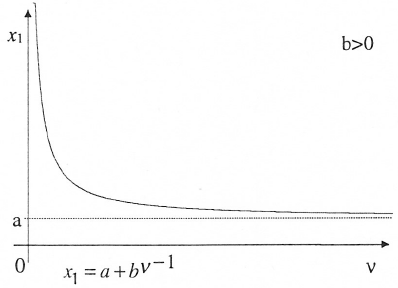
Abbildung 12-6: Inverses Modell mit einer Konstanten
|
|
|
Abbildung 12-7: Logarithmisches Modell mit einer Konstanten
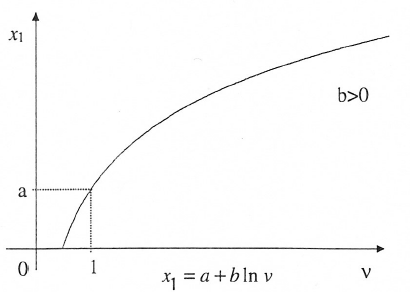
Funktionen, die in den Parametern linear sind, lassen sich durch eine Transformation der unabhängigen Variablen leicht linearisieren und können danach einer linearen Regressions- und Korrelationsanalyse unterzogen werden.
d) Intrinsisch lineare Funktionen
Eine weitere Klasse von relevanten Funktionen sind zwar nicht linear in den Parametern, lassen sich aber durch Transformationen der abhängigen Variablen ebenfalls linearisieren.
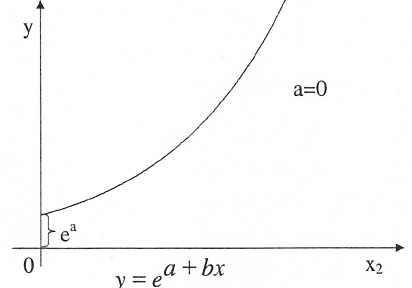
Dazu betrachten wir sog. Potenz-Modelle, bei denen der Regressionskoeffizient im Exponenten der unabhängigen Variablen steht, und ein Exponential-Modell, mit der unabhängigen Variablen im Exponenten :
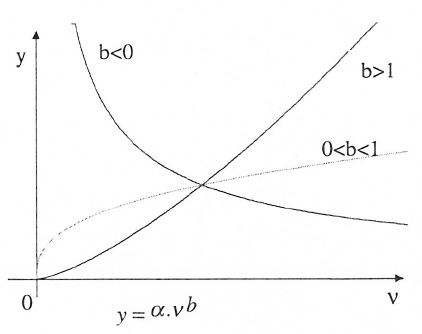
Abbildung 12-8: Modelle mit einer Potenzfunktion
|
|
Abbildung 12-9: Modell mit einer Wachstumsfunktion
|
|
|
3. Die Linearisierungen der Regressionsfunktionen
a) Die Linearisierung bei Linearität in den Parametern
In dieser Klasse von Modellen erfolgt die Linearisierung über eine Transformation der unabhängigen Variablen. Praktisch bedeutet das, dass die Ausgangsvariable v in die Modellvariable x2 bzw. x3 umgerechnet wird. Diese erfolgt modellspezifisch und ist nachfolgend demonstriert.
Die Linearisierung des quadratischen Modells
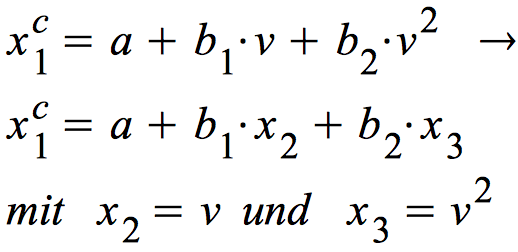
Die Linearisierung des inversen Modells
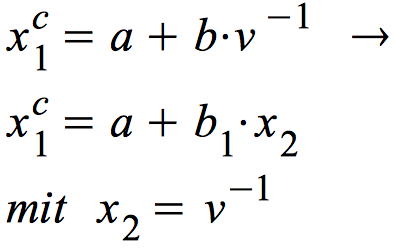
Die Linearisierung des logarithmischen Modells
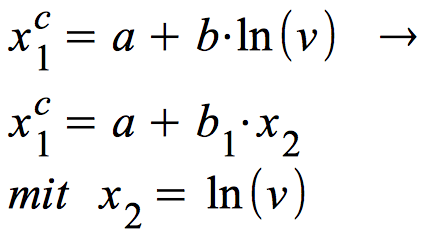
b) Die intrinsische Linearisierung
Für die in 2.d) präsentieren Klasse von Modellen erfolgt die Linearisierung über eine Transformation der abhängigen Variablen. Praktisch bedeutet das, dass die Ausgangsvariable y in die Modellvariable x1 umgerechnet wird. Diese erfolgt wieder modellspezifisch und ist nachfolgend demonstriert.
4. Die Berechnung des Regressions- und Korrelationsmodells
a) Die Berechnung der Regressionsparameter
Nach der Linearisierung der Modellkomponenten erfolgt die Ermittlung der Regressionsfunktion wie im einfachen linearen Modell nach der Methode der kleinsten Quadrate. Dies kann im Vergleich der Abb. 12-4 und 12-9 unmittelbar veranschaulicht werden.
Abbildung 12-4: Lineare und quadratische Regressionsfunktion für die Ausgangsdaten
|
|
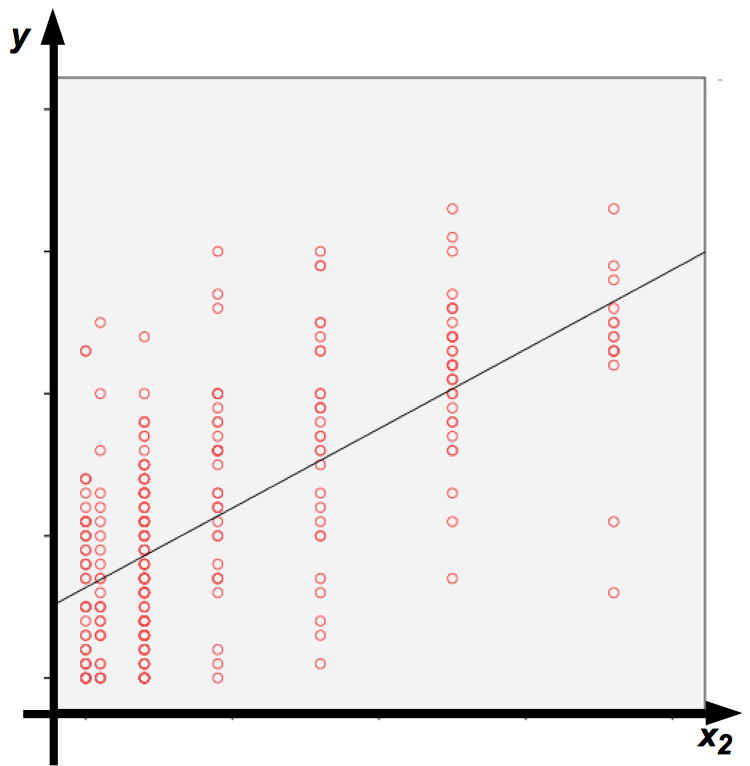
Abbildung 12-9: Lineare Regressionsfunktion nach der Transformation x2 = v2
|
|
|
Mit x2 = v2 werden die Ursprungswerte der Variablen v (0...6) in die Wertereihe (0, 1, 4, 9, 16, 25, 36) transformiert, für die sich dann eine lineare Beziehung ergibt.
Auf der Basis der transformierten Variablen ergeben sich die Werte der Regressionsparameter nach den in Kap. 11 abgeleiteten Formeln. Dies gilt sowohl für Modelle mit in den Parametern linearen Funktionen wie für Modelle mit intrinsisch linearen Funktionen.
b) Die Berechnung und Interpretation des Korrelations- und Determinationskoeffizienten
Die Berechnung der Koeffizienten:
Auf der Basis der transformierten Variablen ergeben sich die Werte der beiden Koeffizienten ebenfalls nach den in Kap. 11 für R und R-Quadrat abgeleiteten Formeln. Dies gilt sowohl für Modelle mit in den Parametern linearen Funktionen wie für die Modelle mit intrinsisch linearen Funktionen. Allerdings unterscheiden sich für die beiden Modelle die bekannten Möglichkeiten der Interpretation der Determinationskoeffizienten.
Die Interpretation der Determinationskoeffizienten:
Im Modell mit in den Parametern linearen Funktionen erfolgt eine Transformation der unabhängigen Variablen. Davon bleibt die Verteilung der abhängigen Variablen insbes. deren Varianz unberührt. Allerdings erhöht die nicht-lineare Funktion im transformierten Modell den Anteil der erklärten Varianz. Dies drückt der Determinationskoeffizient im nicht-linearen Modell ebenso aus wie im linearen.
Im Modell mit intrinsisch linearen Funktionen erfolgt eine Transformation der abhängigen Variablen. Davon wird die Verteilung der abhängigen Variablen ebenso wie deren Varianz tangiert. In diesem Modell drückt der Determinationskoeffizient deshalb nur den Anteil der erklärten Varianz der transformierten Variablen und nicht mehr den der Ursprungsvariablen aus.
|



