 |
Standardisierte Regressionen mit SPSS - Beispiele und Aufgaben im Modul XII-2 Regression und Korrelation mit standardisierten Variablen
1. Beispielsrechnungen mit SPSS
Nachstehend wird am Beispiel der Datei Partizipation_1.sav und der dort enthaltenen, metrisch-skalierten Variablen Partizipationsprofil und Partizipationspotential gezeigt, wie mit SPSS Regressions- und Korrelationsanalysen mit standardisierten Variablen graphisch veranschaulicht und rechnerisch durchgeführt werden und wie die Ergebnisse im Hinblick auf Richtung und Stärke des Zusammenhangs der Variablen zu interpretieren sind.
Um die nachfolgenden Aufgaben bearbeiten zu können, wird nochmals gezeigt, wie die Ausgangsvariablen mit SPSS standardisiert werden:
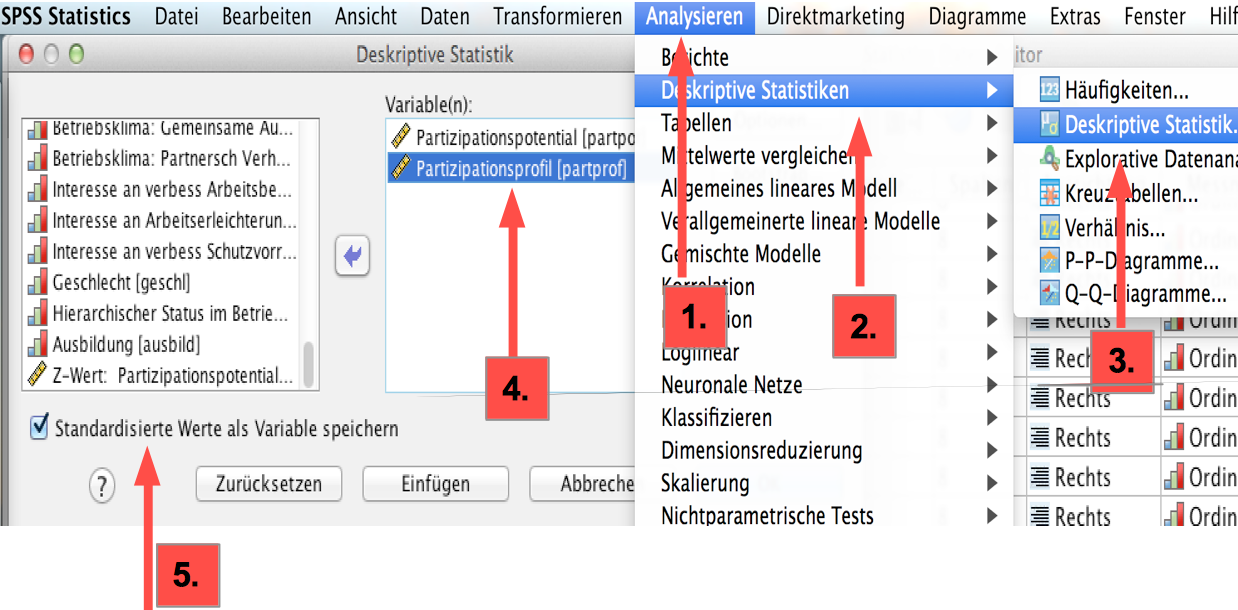
Screenshot 12-6: Standardisierung der Ausgangsvariablen mit SPSS
|
|
Erläuterungen:

|
|
|
Im Folgenden werden zuerst die Analysen an Hand von Streudiagrammen mit dem Analysetool "Grafik" veranschaulicht und danach mit den Programmpaketen "Regression" rechnerisch durchgeführt und tabellarisch präsentiert.
a) Die graphische Regressions- und Korrelationsanalyse
Dazu wird wieder die Prozedur "Streu-/Punktdiagramm" aufgerufen und das Ergebnis in Form eines Streuungsdiagramms mit eingefügter Regressionsfunktion dargestellt.
Screenshot 12-7: Im Grafik-Modul das Streuungsdiagramm anfordern
Screenshot 12-8: Im Grafik-Editor die Regressionsfunktion eintragen
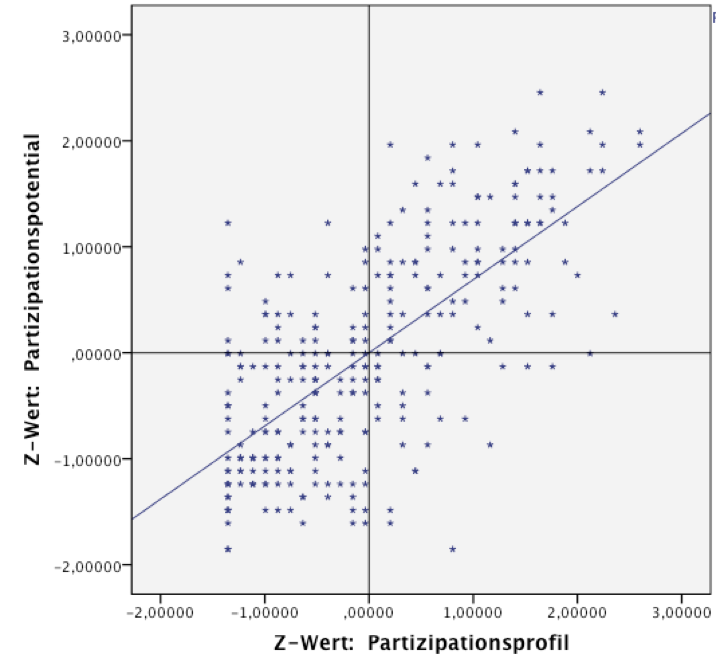
Zur Bearbeitungen der Grafik im Grafik-Editor vgl. Kap. 11-3.
Nach der rechnerischen Regressionsanalyse werden die Ergebnisse interpretiert und mit den Ergebnissen einer Regressionsanalyse zwischen den Ausgangsdaten verglichen.
b) Die rechnerische Regressionsanalyse
Die Regressionsanalyse mit SPSS
|
Screenshot 12-9: Im Regressionsmodul die Regressions- und Korrelationsanalyse anfordern
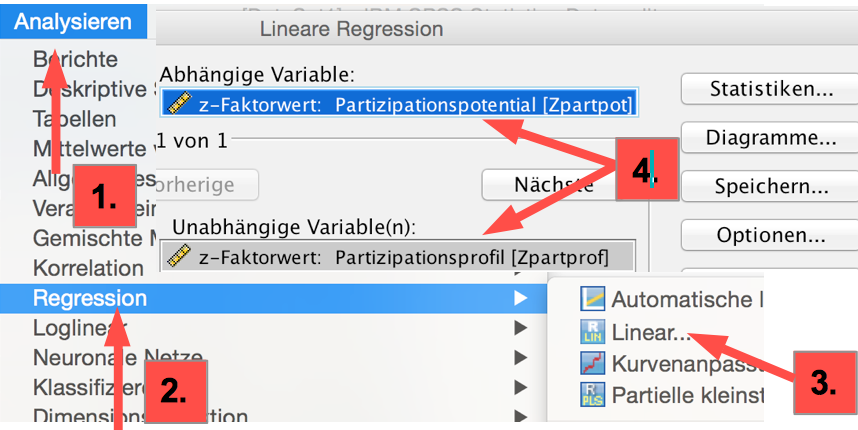
1. Im Menue die Programmkomponente "Analysieren" markieren,
2. "Regression“ auswählen,
3. "Lineare Regression" spezifizieren,
4. Die z - Variablen eintragen.
|
|
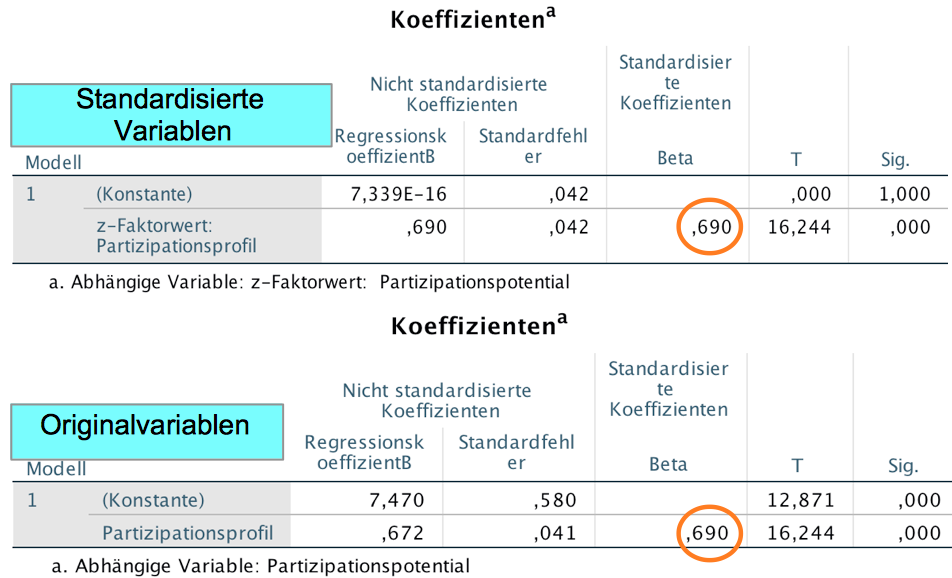
Screenshot 12-10: Die Ergebnisse der Regressionsanalysen vergleichen
|
|
|
Interpretation der Koeffizienten der standardisierten Variablen
Die Regressionskonstante weist einen Betrag von 7,339 E-16 auf, das ist ein Wert, der mit 7,339/ 1016 sehr nahe bei "0" liegt.
Der Regressionskoeffizient beträgt 0,69 und ist identisch mit dem standardisierten Koeffizienten "Beta". Er besagt, dass die abhängige Variable im Durchschnitt um 0,69 Standardabweichungen wächst, wenn die unabhängige um eine Standardabweichungen zunimmt. Diese Aussage gilt auch für die Ausgangsvariablen.
Vergleich der Koeffizienten der standardisierten Variablen mit den Koeffizienten der Regression der Ausgangsvariablen:
Die Ausgabetabelle für die Ausgangsdaten enthält auch den Wert des standardisierten Regressionskoeffizienten "Beta", der mit den entsprechenden Ergebnissen für die standardisierten Variablen übereinstimmt.
Zur Interpretation der nicht standardisierten Koeffizienten vgl. das Beispiel in Kap. 11-3, Regressions- und Korrelationsanalysen mit SPSS
c) Die Ergebnisse zur Korrelationsanalyse vorstellen und vergleichen
Die Korrelationsanalysen mit SPSS
|
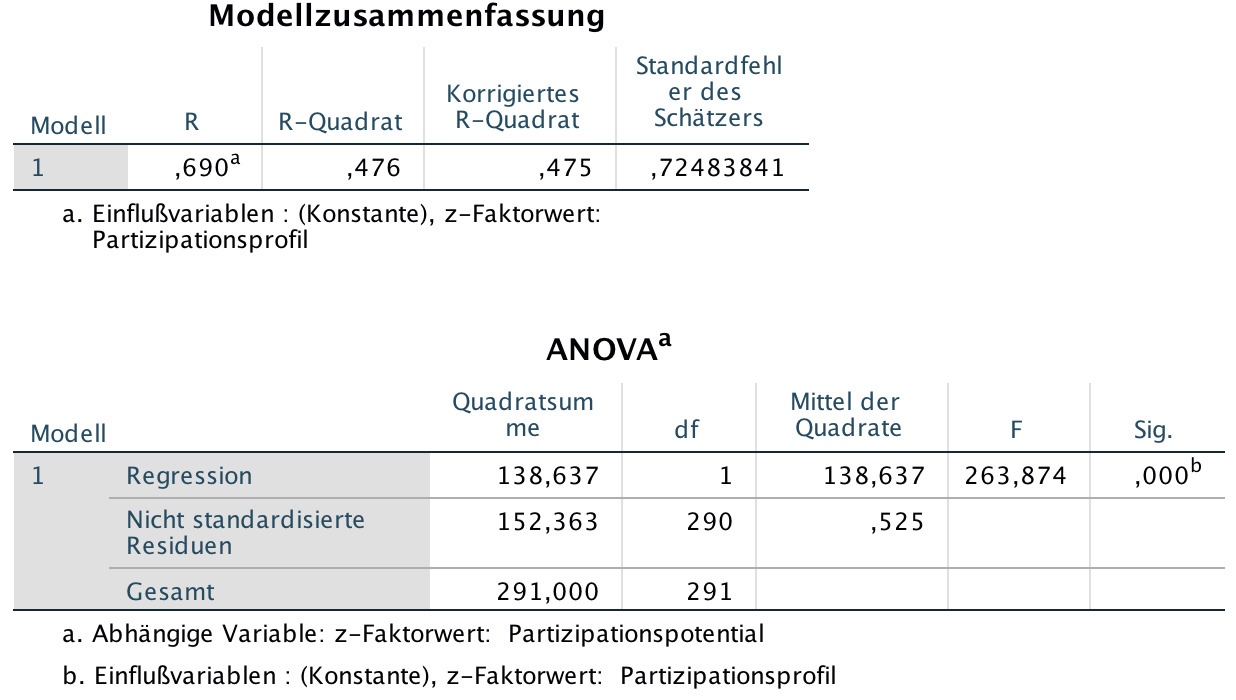
Screenshot 12-11: Die Ergebnisse der Korrelationsanalyse zwischen den standardisierten Variablen
|
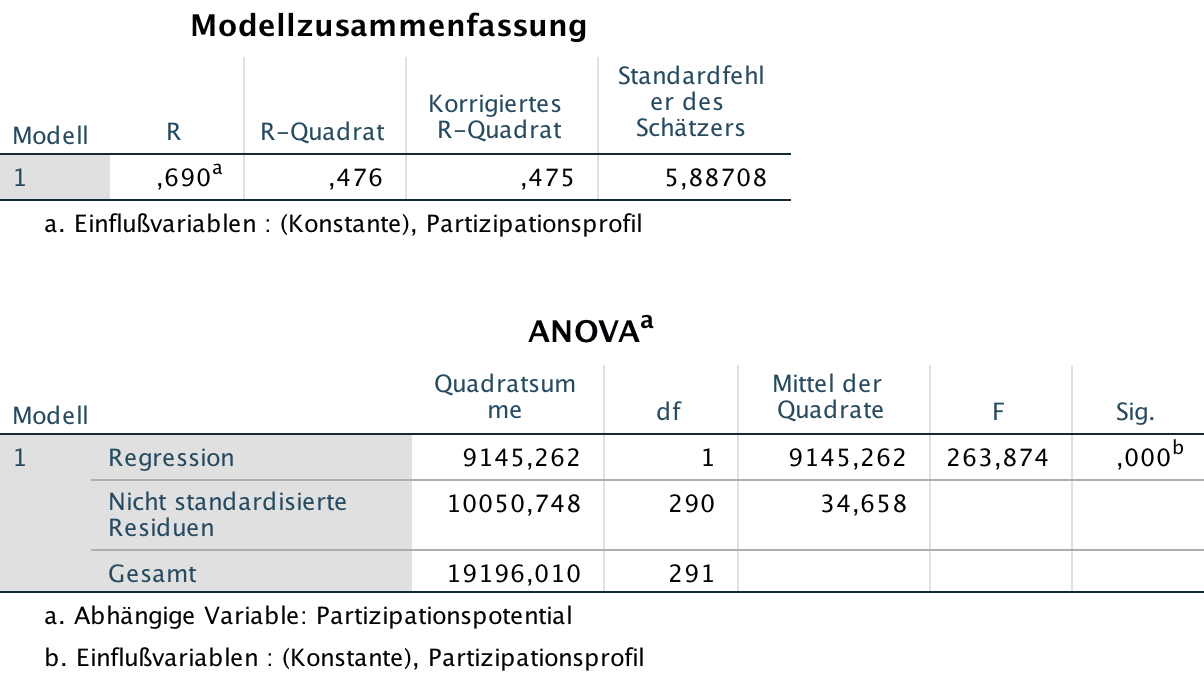
| Screenshot 12-12: Die Ergebnisse der Korrelationsanalyse zwischen den Ausgangs-Variablen
|
Interpretation der Koeffizienten der standardisierten Variablen
Die Modellzusammenfassung weist einen Betrag für R von 0,69 auf. Dieser entspricht dem Wert des standardisierten Regressionskoeffizienten und dem Beta-Wert (vgl. Screenshot 12-10).
In der ANOVA-Tabelle beträgt die Gesamtsumme der Abstandsquadrate 291. Das entspricht dem n-1 fachen Wert der Varianz der standardisierten Variablen von "1".
Vergleich der Korrelation der standardisierten Variablen mit der Korrelation der Ausgangsvariablen:
Die Modellzusammenfassungen enthalten die Werte für R und R-Quadrat und bestätigen die Identität der Koeffizienten für die Korrelation zwischen den standardisierten Variablen und zwischen den Ausgangsvariablen.
Zur Interpretation von R und R-Quadrat vgl. das Beispiel in Kap. 11-3.
Anmerkung: Darstellung und Interpretation der induktiven Aspekte der Regressios- und Korrelationsanalyse finden sich in ViLeS 2, Modul Regressionsanalyse mit SPSS .
2. Aufgaben
a) Die Ausgangsdaten
Analysieren Sie unter Verwendung der Datei Partizipation_1.sav mit SPSS den Zusammenhang zwischen den standardisierten Variablen tatsächlicher Beteiligung (z-partprof) und Geschlecht (z Geschl) sowie zwischen den standardisierten Variablen gewünschte Beteiligung (z-partpot) und Geschlecht (z Geschl).
Standardisieren Sie dazu die beiden Variablen nach dem in Screenshot 12-6 demonstrierten Verfahren.
b) Die Aufgabenstellung
Führen Sie die Regressions- und Korrelationsanalyse für die beiden Variablenpaare durch und interpretieren Sie die Ergebnisse.
Vergleichen Sie die, in den beiden Modellen ermittelten Beta-Koeffizienten und formulieren Sie eine Aussage darüber, auf welche abhängige Variable die Variable Geschlecht den größten Einfluss hat.
Vergleichen Sie anhand der Beta-Koeffizienten den Einfluss der Variablen Geschlecht und den Einfluss der Variablen tatsächliche Beteiligung auf die Variablen gewünschte Beteiligung und formulieren Sie eine Aussage darüber, welche unabhängige Variable den stärksten Einfluss auf die gewünschte Beteiligung hat.
|



