 |
Konzepte und Definitionen im Modul XII-2 Regression und Korrelation mit standardisierten Variablen
1. Die standardisierten Variablen zj (j = 1,2)
a) Definition und Funktion standardisierter Variablen
Definition der standardisierten Variablen:
Eine standardisierte Variable weist einen Mittelwert von "0" und eine Standardabweichung von "1" auf.
Eine beliebige Variable xj kann in eine standardisierte Variable zj transformiert werden, dabei führt die Standardisierung zu einer Rescalierung der Ausgangswerte.
Die Funktion der Standardisierung:
Aus verschiedenen Gründen kann es sinnvoll sein, eine beliebige Variable xj in eine standardisierte Variable zj zu transformieren:
So lässt sich die formale Betrachtung von komplexen statistischen Zusammenhängen wesentlich vereinfachen, wenn man sie für standardisierte Variablen durchführt. Insofern bereitet dieser Abschnitt die folgenden Methodenbeschreibungen vor.
Wie nachstehend gezeigt wird, eignet sich der standardisierte Regressionskoeffizient besonders für den Vergleich des Einflusses unterschiedlicher Regressoren.
Darüber hinaus stehen standardisierte Variablen im Zentrum der schließenden Statistik (vgl.: ViLeS 2)
Beispiel einer standardisierten Variablen:
Als Beispiel betrachten wir die skalierte Variable zPartprof, die sich aus der Variablen Partprof der tatsächlichen Beteiligung ableiten lässt:
Abbildung 12-2: Die Verteilung der standardisierten Variablen zPartprof
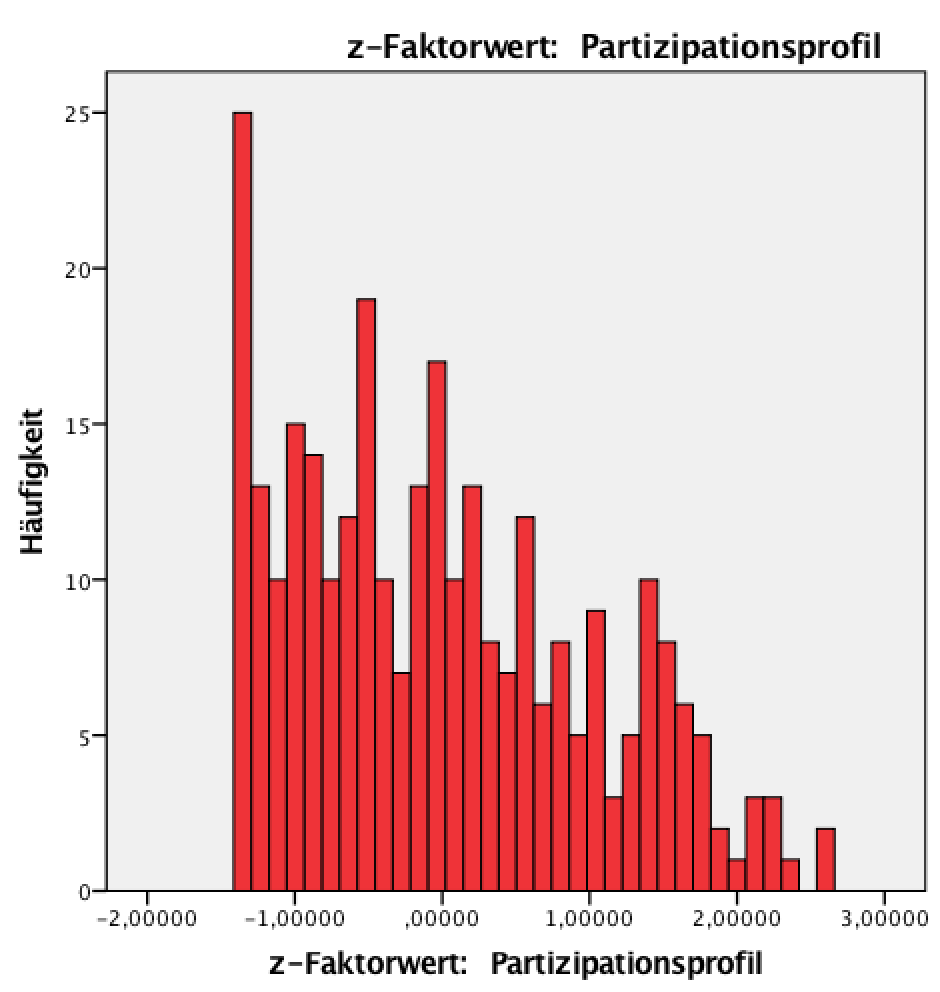
Die Beobachtungen streuen nun um den Mittelwert von "0". Die Skaleneinheit beträgt eine Standardabweichung und die Skalenwerte reichen von -2 bis +3, d.h. die Abweichungen vom Mittelwert werden nicht mehr in den ursprünglichen Einheiten gemessen sondern in der Einheit "Standardabweichung". Die innere Struktur der Verteilung bleibt hingegen unverändert.
b) Die Standardisierung der Variablen xj
Wir erhalten die standardisierte Variable zj über:
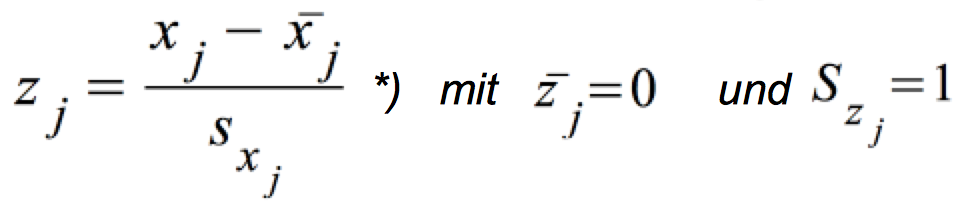
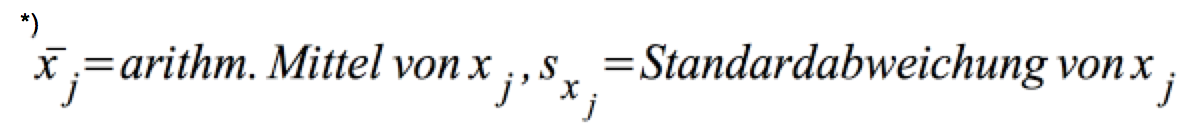
2. Regression zwischen standardisierten Variablen
a) Die Regressionsfunktion
-
Die Funktionsform:
Die Regressionsfunktion z1c = f(z2)
lautet:
z1c = a* + b* · z2 , mit a* und b* wie folgt:
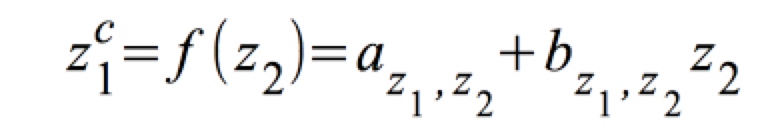
Zu den Formeln für die Regressionsparameter vgl. b).
-
Die Darstellung im Streuungsdiagramm:
Das Zentrum der Punktwolke liegt im 0-Punkt des Koordinatensystems und die Funktion verläuft durch diese Mitten der Verteilungen:
Abbildung 12-3: Die Funktion im Koordinatensystem
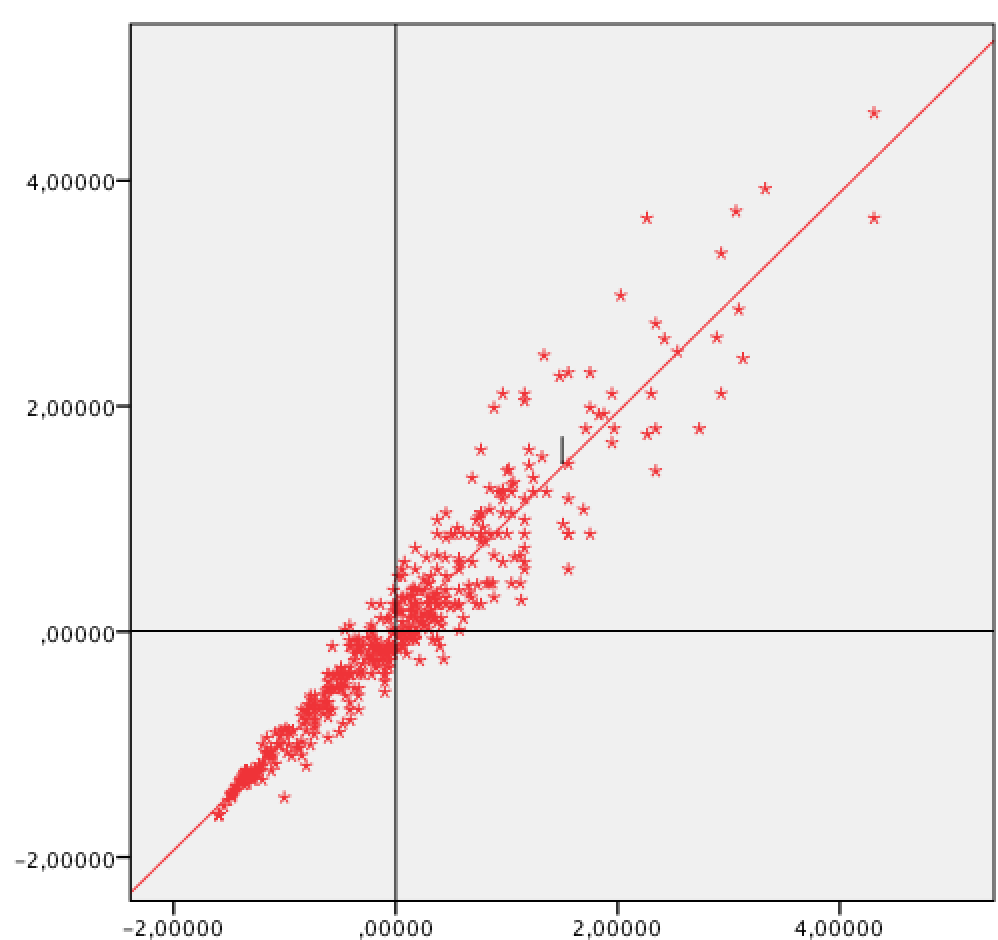
Die Fehlerquadrate werden minimiert, wenn die Regressionsfunktion, wie in Abb. 12-3 gezeigt, durch die arithmetischen Mittel der beiden Verteilungen verläuft.
b) Die Regressionsparameter
3. Der Korrelations- und Determinationskoeffizient
a) Die Ermittlung von R und R2
Wie schon bei der rechnerischen Bestimmung der Regressionsparameter stützt sich die Berechnung des Korrelations- und des Determinationskoeffizienten auf die entsprechenden Formeln in Kap. 11.
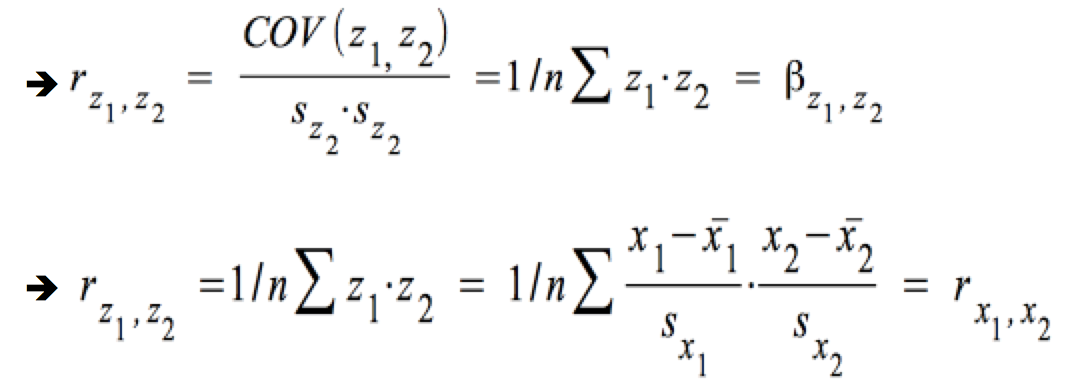
b) Die Interpretation von R und R2
R2 verkörpert das Ausmaß der Varianz von z1, das durch den Regressor z2 erklärt wird. Dabei sind zwei Aspekte von zentraler Bedeutung:
Im Falle standardisierter Variablen entsprechen sich Korrelationskoeffizient und Regressionkoeffizient.
Der Korrelationskoeffizient zwischen standardisierten Variablen entspricht dem Korrelationskoeffizient zwischen nicht-standardisierten Variablen.
Dies ist auschlaggebend für Regressions- und Korrelationsanalysen auf der Basis standardisierter Variablen, weil somit die Standardisierung keinen Einfluss auf die Stärke des Zusammenhangs hat.
|



