 |
Regressions- und Korrelationsanalysen mit SPSS im Modul XI-3 Eigene Analysen und Interpretationen
1. Vorbemerkungen
Nachstehend wird am Beispiel der Datei Partizipation_1.sav und der dort enthaltenen, metrisch-skalierten Variablen Partizipationsprofil und .potential gezeigt, wie mit SPSS Regressions- und Korrelationsanalysen graphisch veranschaulicht und rechnerisch durchgeführt werden und wie die Ergebnisse im Hinblick auf Richtung und Stärke des Zusammenhangs der Variablen zu interpretieren sind.
Dazu werden zuerst die Analysen an Hand von Streudiagrammen mit dem Analysetool "Grafik veranschaulicht und danach mit den Programmpaketen "Regression" und "Korrelation" rechnerisch durchgeführt und ausführlich tabellarisch präsentiert. Die Ergebnisse, die bereits in den vorangegangenen Modulen dieses Kapitels vorgestellt wurden, werden schließlich vertieft inhaltlich diskutiert.
2. Die graphische Regressions- und Korrelationsanalyse
a) Die Prozedur "Streudiagramme" aufrufen
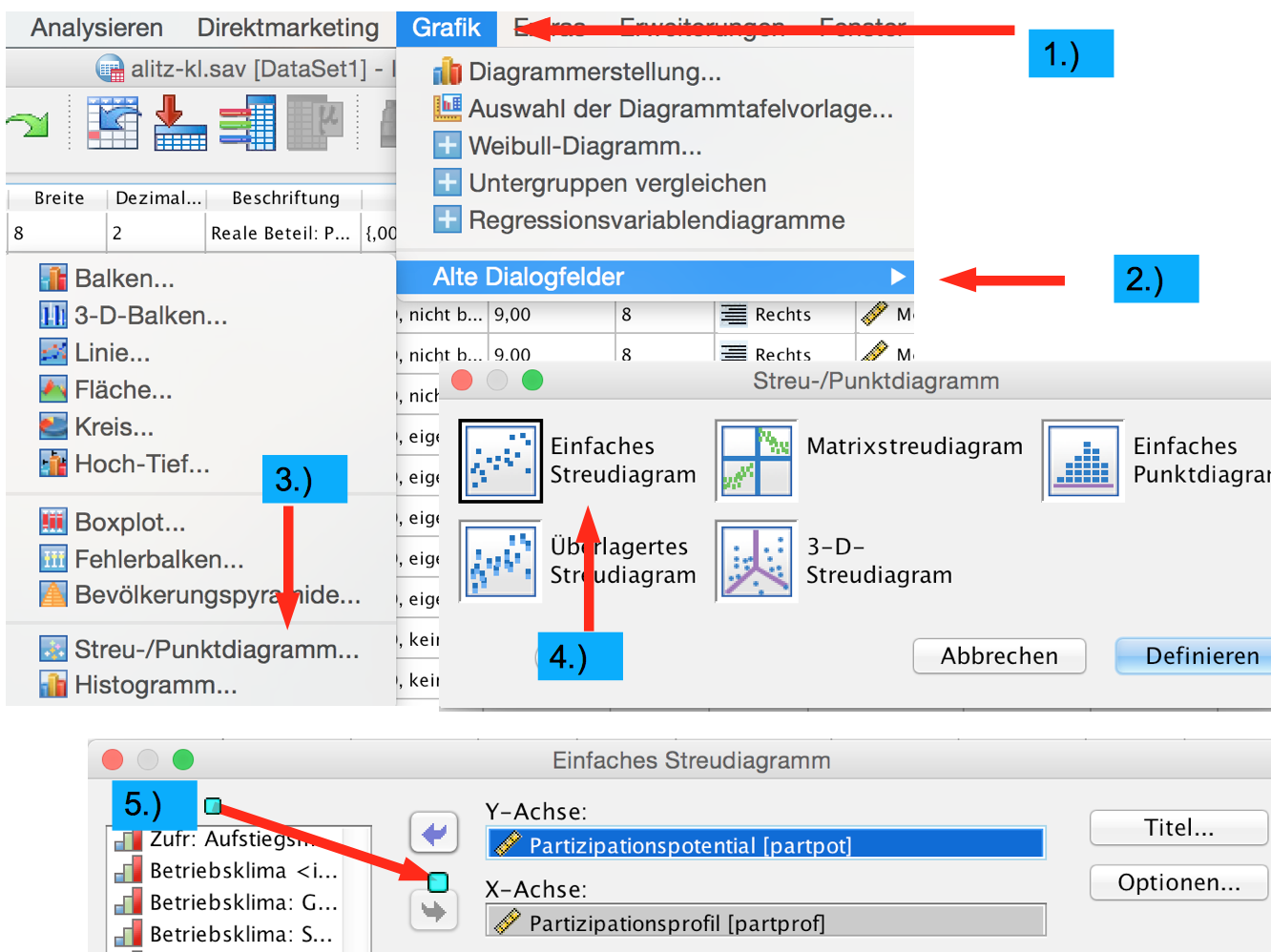
Dazu wird im ersten Schritt die Prozedur "Streu-/Punktdiagramm" über folgende Eingaben aufgerufen:
Screenshot 11-1: Mit SPSS Streudiagramme aufrufen
b) Das Streuungsdiagramm im Grafik-Editor bearbeiten
In den nächsten Schritten wird die Regressionsfunktion in die Grafik eingefügt und die Grafik unter Analyseaspekten modelliert.
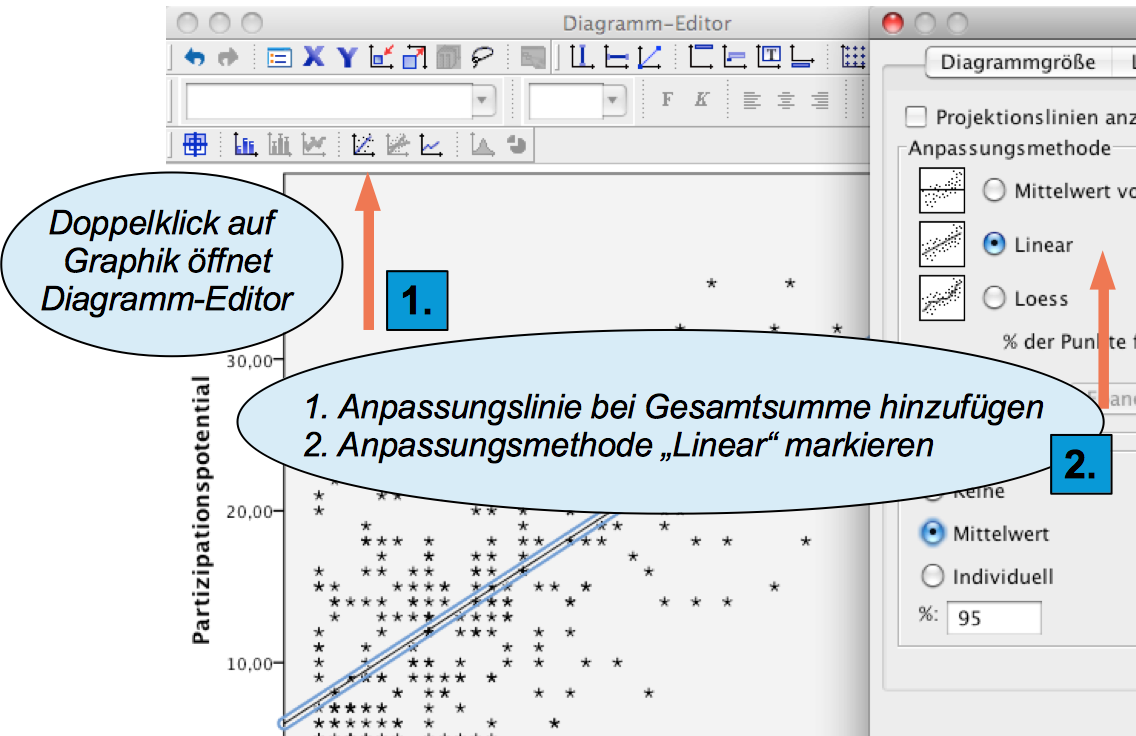
Den Grafik-Editor aufrufen und die Regressionsfunktion erzeugen
Um die Regressionsfunktion in die Punktwolke einzuzeichnen und die Achsen korrekt zu verorten, sind die beiden folgenden Prozeduren vorzunehmen:
|
Screenshot 11-2: Im Grafik-Editor die Regressions- funktion anfordern
|
|
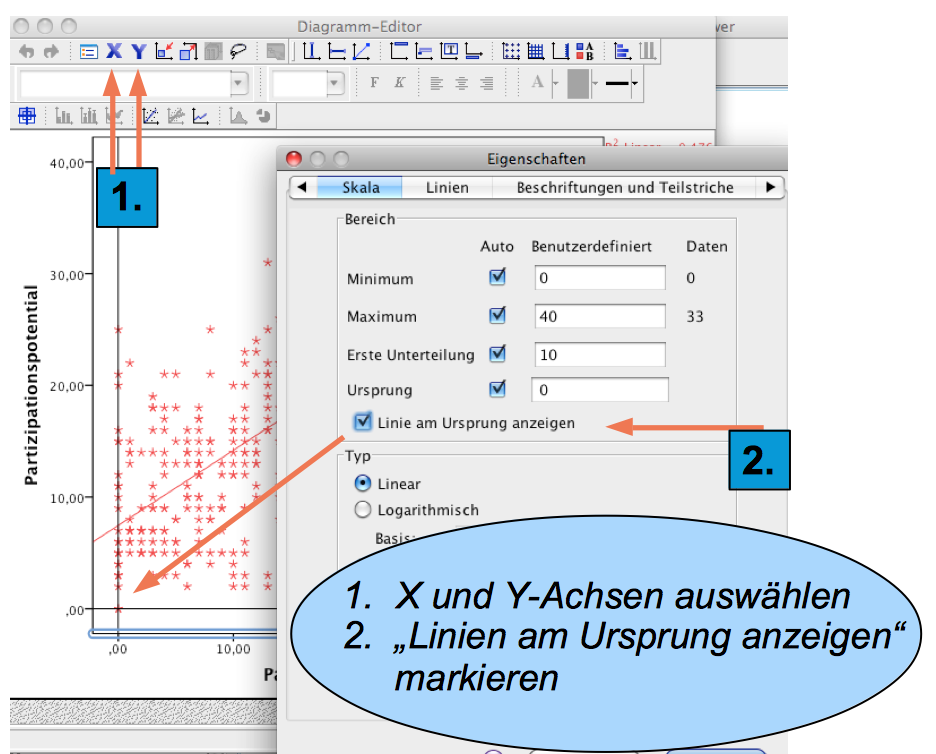
Screenshot 11-3: Die Koordinatenachsen in den "Null"-Punkt" legen
|
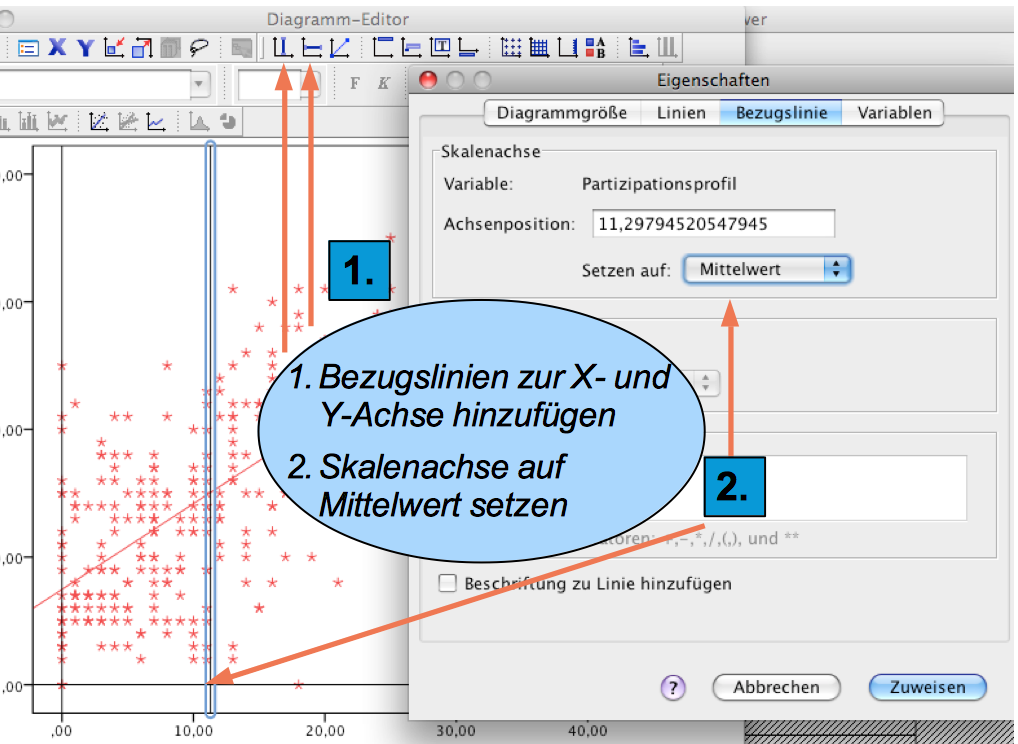
Analyseaspekte durch Hilfs-Linien veranschaulichen
Durch eine zusätzliche Bearbeitung der Grafik können weitere Aspekte des Zusammenhangs zwischen den Variablen herausgearbeitet werden.
|
Screenshot 11-4: Mittelwert-Linien einzeichnen
|
|
Screenshot 11-5: 45°-Linie einzeichne
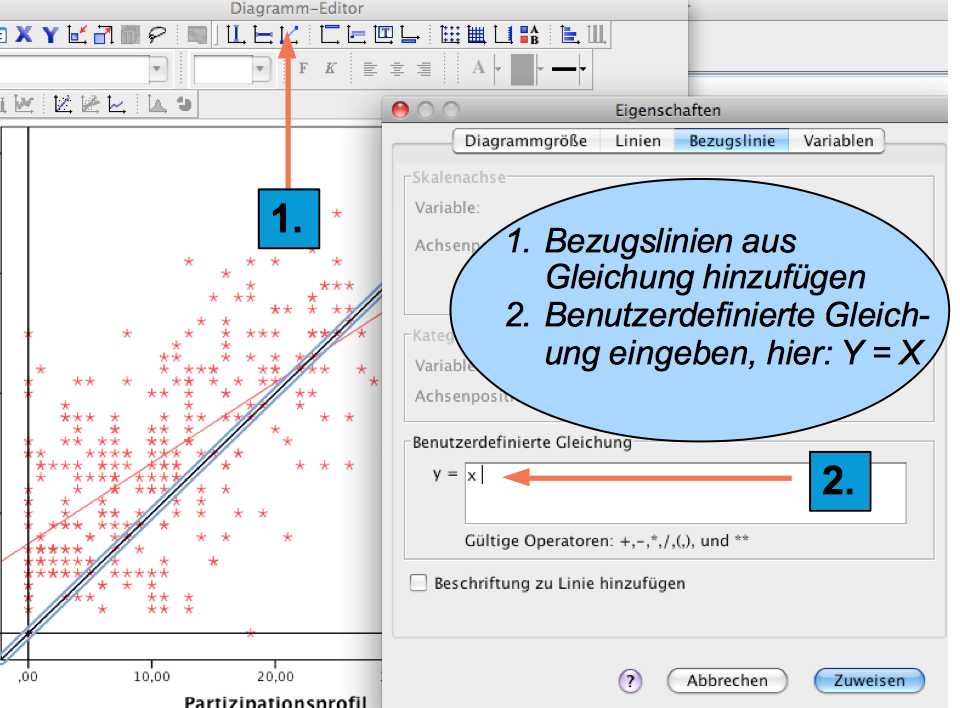
|
Der Grafik-Editor bietet eine Vielzahl von grafischen und redaktionellen Gestaltungsmöglichkeiten, wie farbliche oder textliche Veränderungen, die hier nicht nicht weiter vorgestellt werden können. Sie erschließen sich durch Anklicken der jeweiligen Elemente der Grafik von selbst.
c) Die Ergebnisse vorstellen und interpretieren
|
Screenshot 11-6: Das modifizierte Streudiagramm
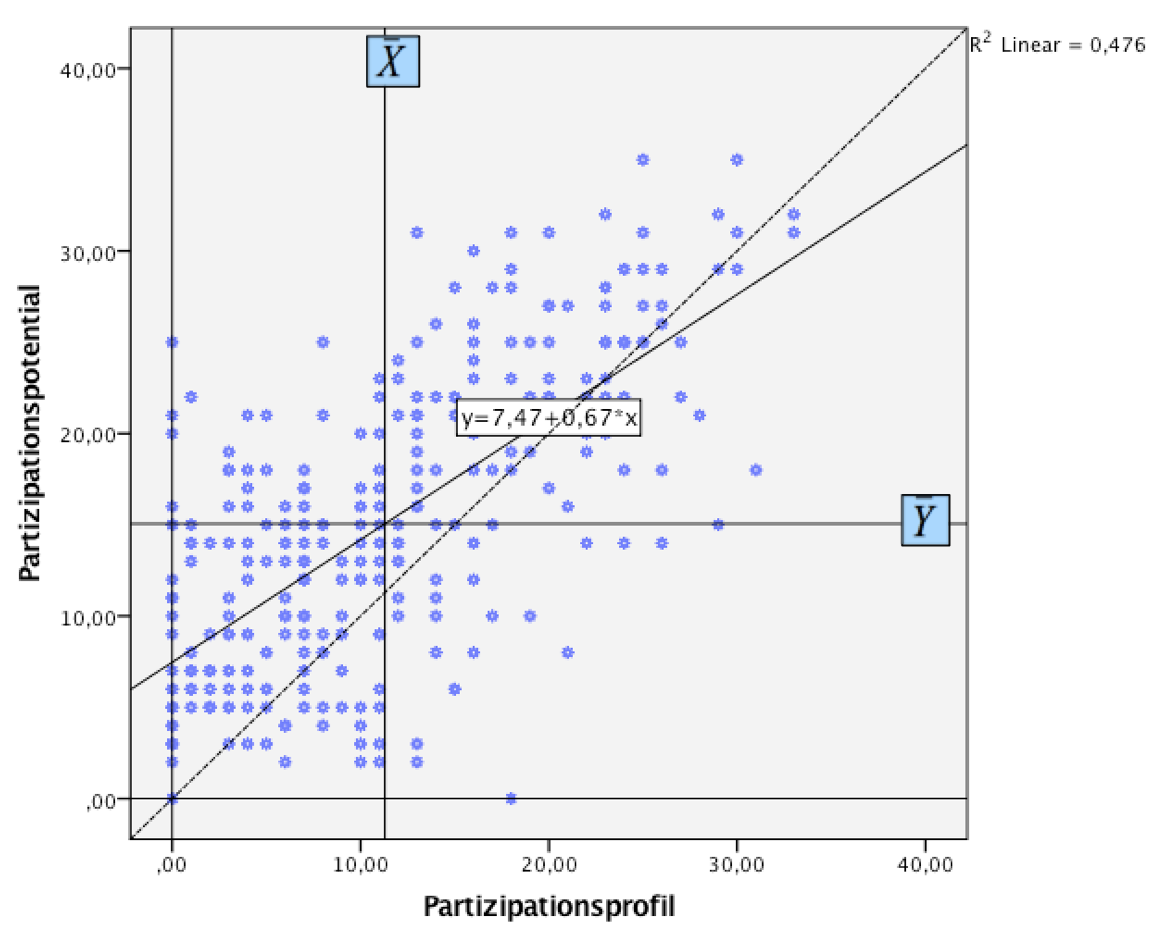
|
| 
|
3. Die Regressions- und Korrelationsanalyse mit der Prozedur "Regression"
Mit der Prozedur "Regression" wird in SPSS nicht nur eine Regressionsanalyse sondern auch eine Korrelationsanalyse durchgeführt. Ein Streuungsdiagramm wird nicht erstellt, allerdings ein Diagramm, dass die Verteilung der Fehler beinhaltet.
a) Die Prozedur "Regression" aufrufen
Screenshot 11-7: Die Regressionsanalyse anfordern


b) Die Ergebnisse der Regressionsanalyse vorstellen und interpretieren
|
Screenshot 11-8: Die Ergebnisse der Regressionsanalyse
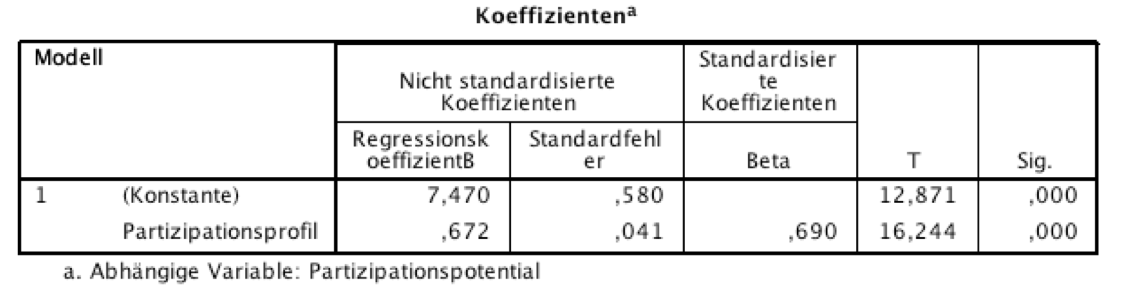
|
|

|
Anmerkung: Darstellung und Interpretation der induktiven Aspekte der Regressios- und Korrelationsanalyse finden sich in Regressionsanalyse mit SPSS .
c) Die Ergebnisse der Korrelationsanalyse vorstellen und interpretieren
|
Screenshot 11-9: Die ANOVA-Ergebnisse der Korrelationsanalyse
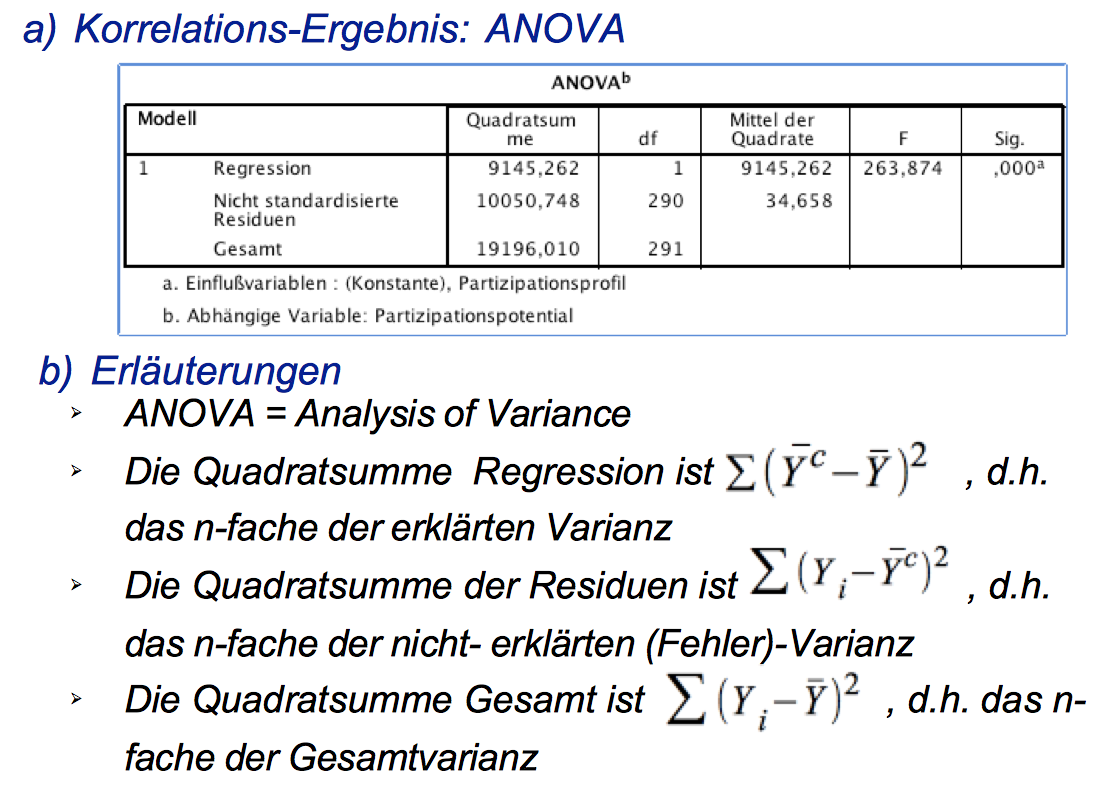
|
| Screenshot 11-10: Die Maßzahlen der Korrelationsanalyse

|
Anmerkung: Zu den induktiven Aspekte der Regressios- und Korrelationsanalyse vgl. die Anmerkung unter b).
d) Die Fehleranalyse anfordern und interpretieren
|
Screenshot 11-11: Das Fehlerdiagramm anfordern
|
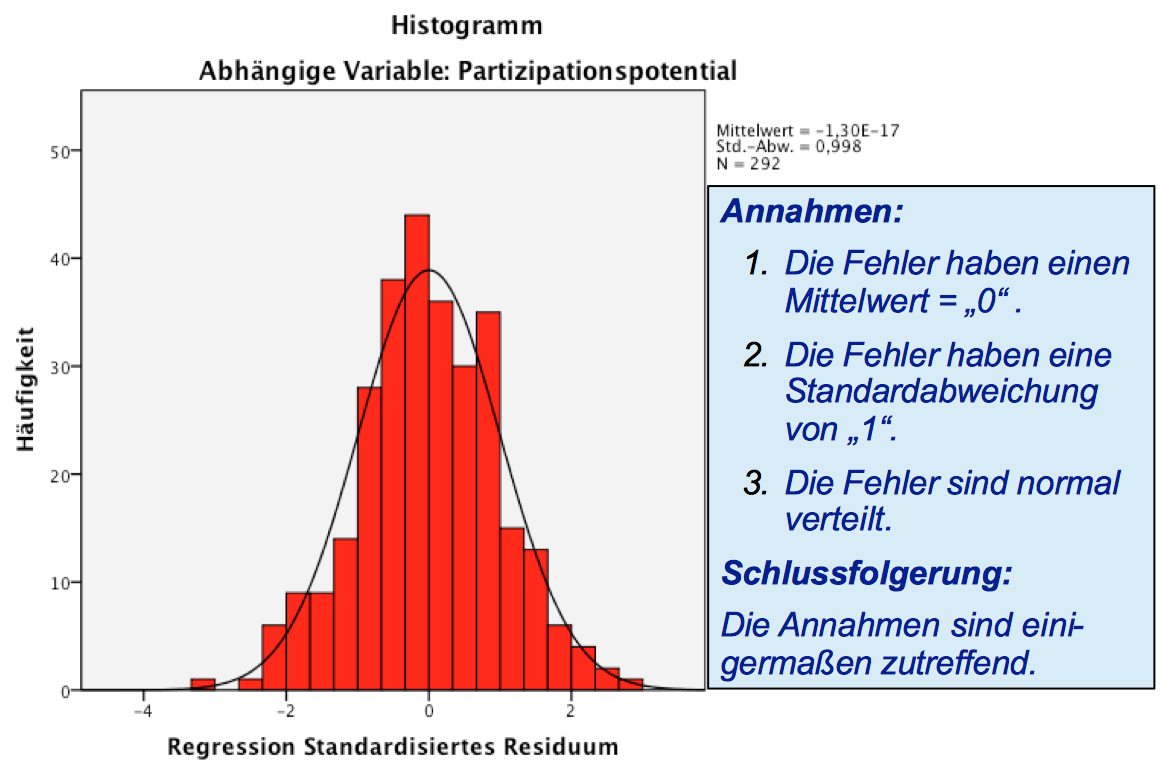
| Screenshot 11-12: Das Fehlerdiagramm interpretieren
|
4. Die Korrelationsanalyse mit der Prozedur "Korrelation"
Mit der Prozedur "Korrelation" wird in SPSS nur eine einfache Korrelationsanalyse durchgeführt, allerdings gemeinsam für eine Reihe von Variablen. Damit können die Zusammenhänge in einem Datensatzes in Form einer Korrelations-Matrix dargestellt werden.
a) Die Prozedur "Korrelation" aufrufen
Im Folgenden sollen die Beziehungen zwischen den Kompetenzen in den einzelnen Entscheidungsbereichen untersucht werden. Dazu soll eine Korrelationsmatrix für die Entscheidungsbereiche "Reale Beteiligung bei Personalentscheidungen".... "Reale Beteiligung bei Entscheidungen über den Arbeitsprozess-Ablauf" erstellt werden
Screenshot 11-13: Die Korrelationsmatrix anfordern
b) Die Korrelationsmatrix vorstellen und interpretieren
|
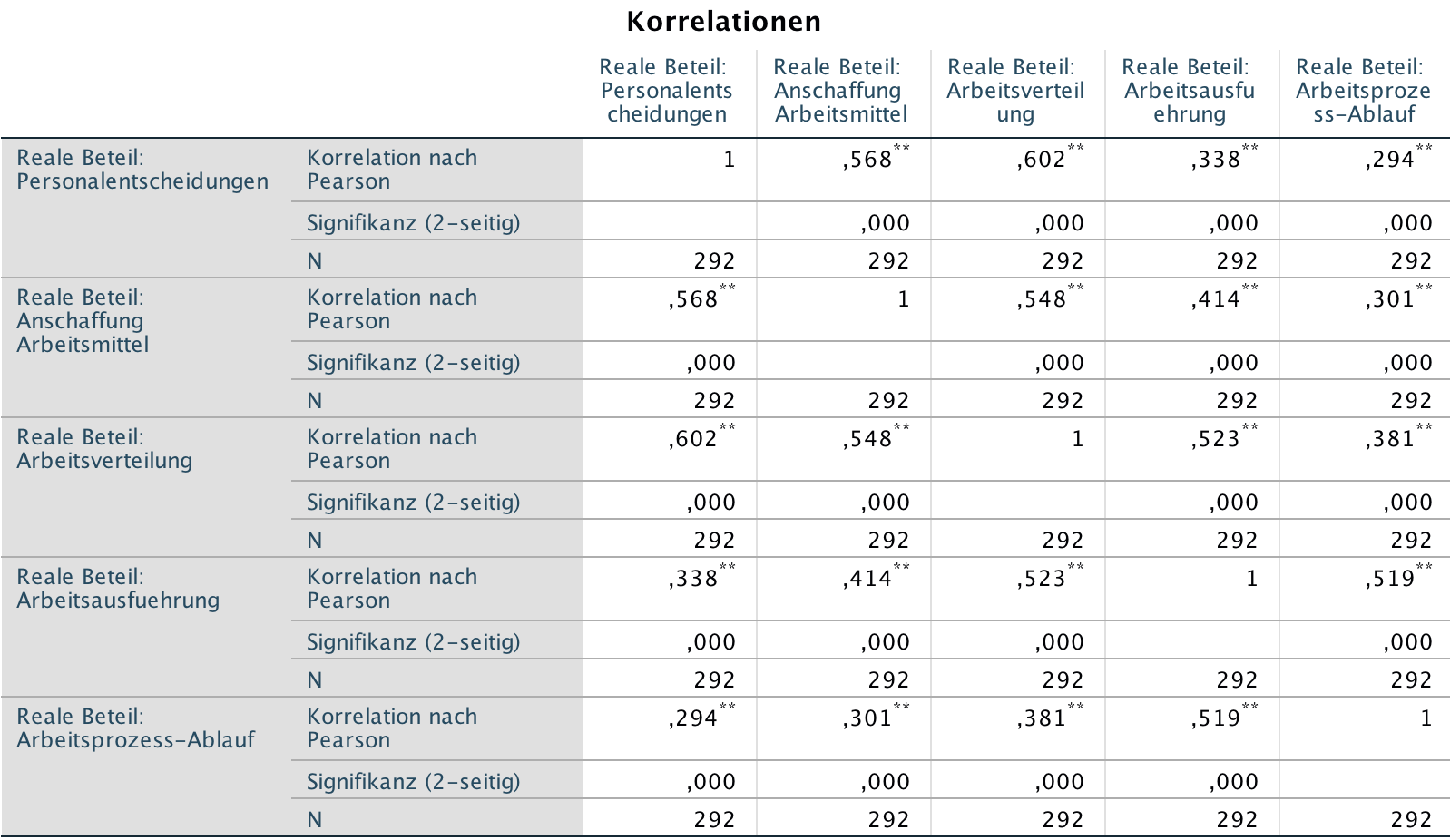
Screenshot 11-14: Die Korrelationsmatrix
|
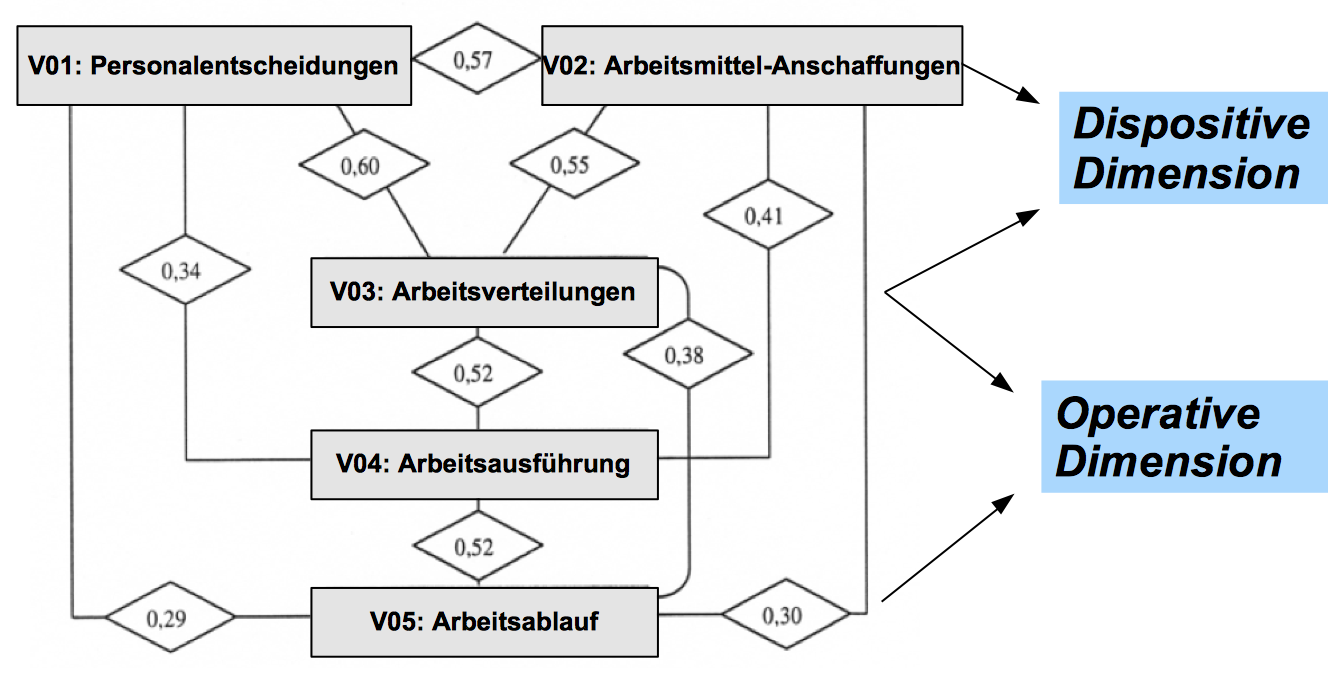
| Abbildung 11-19: Dispositive und operative Dimensionen des Entscheidungssystems
|
Die Aussage der Korrelationsmatrix
Die Korrelationsmatrix ist eine quadratische, um die Hauptdiagonale symmetrische Matrix der Korrelationen.
Sie beinhaltet die Korrelationskoeffizienten ri,j und
für die Variablenpaare (xi, xj) (i,j = 1..k).
Auf der Hauptdiagonalen sind die Korrelationen der Variablen mit sich selbst: rj,i = 1 mit i =j ausgewiesen.
Neben den Koeffizienten sind die Fallzahlen und die Signifikanzen dargestellt. Diese weisen alle einen Betrag von 0,000 auf. Damit sind die Korrelationen alle hoch signifikant, d.h. die Zusammenhänge sind auch in einer hypothetischen Grundgesamtheit gegeben (Zum Begriff der Signifikanz vgl. ViLeS 2, Kap. IV).
Die Interpretation der Korrelationskoeffizienten
Den Beträgen nach liegen die Korrelationen mit Werten zwischen etwa 0,30 und 0,60 im Bereich geringer bis mittlerer Zusammenhänge. Betrachten man Zusammenhänge im Einzelnen so fallen
drei Besonderheiten auf, die in Abb. 11-19 veranschaulicht sind.
Es gibt eine Dreiergruppe von Variablen, die mit Beträgen zwischen 0,55 und 0,60 untereinander verknüpft sind. Es sind dies die Entscheidungsbereiche "Personalentscheidungen", "Anschaffung von Arbeitsmitteln" und "Verteilung der Arbeit", also Entscheidungen im dispositiven Bereich, die üblicherweise dem Mittelmanagement vorbehalten sind.
Daneben sind zwei Paarkonstellationen mit Koeffizienten von 0,52 gegeben. Sie beziehen sich auf Zusammenhänge zwischen den Variablen "Arbeitsverteilung" und "Arbeitsausführung" sowie auf die Variablen "Arbeitsausführung" und "Arbeitsprozess-Ablauf". Damit sind jeweils Bereiche miteinander korreliert, die die Organisation der Arbeitsprozesse betreffen, also eine operative Dimension haben, an der auch die unteren Statusgruppen partizipieren.
Diese Beziehungsgeflechte stehen jeweils für sich, da die restlichen 50% der Zusammenhänge zwischen den Variablen nur Koeffizientenwerte zwischen 0,3 und 0,4 aufweisen.
|



