 |
Konzepte und Definitionen im Modul XI-2 Das einfache lineare Korrelationsmodell
1. Vorüberlegungen
Das einfache lineare Korrelationsmodell ergänzt das lineare Regressionsmodell um die Analyse der Stärke des Zusammenhangs. Unterstellt wird dabei wieder ein einfacher linearer Zusammenhang zwischen einer abhängigen und einer unabhängigen Variablen, wobei es für das Ausmaß der Stärke eines Zusammenhangs unerheblich ist, welche Variable als unabhängige und welche als abhängige Variable behandelt wird.
a) Die Gestalt der Punktwolke
Die ermittelte Regressionsfunktion für sich sagt
noch nichts darüber aus, wie stark der statistische Zusammenhang
zweier Variablen tatsächlich ist. Graphisch lässt sich
die Stärke des Zusammenhanges daran einschätzen, wie eng
oder weit die Punktwolke um die Regressionsgerade streut.
Abbildung 11-9: Streuungsdiagramme und Korrelationsbeziehungen
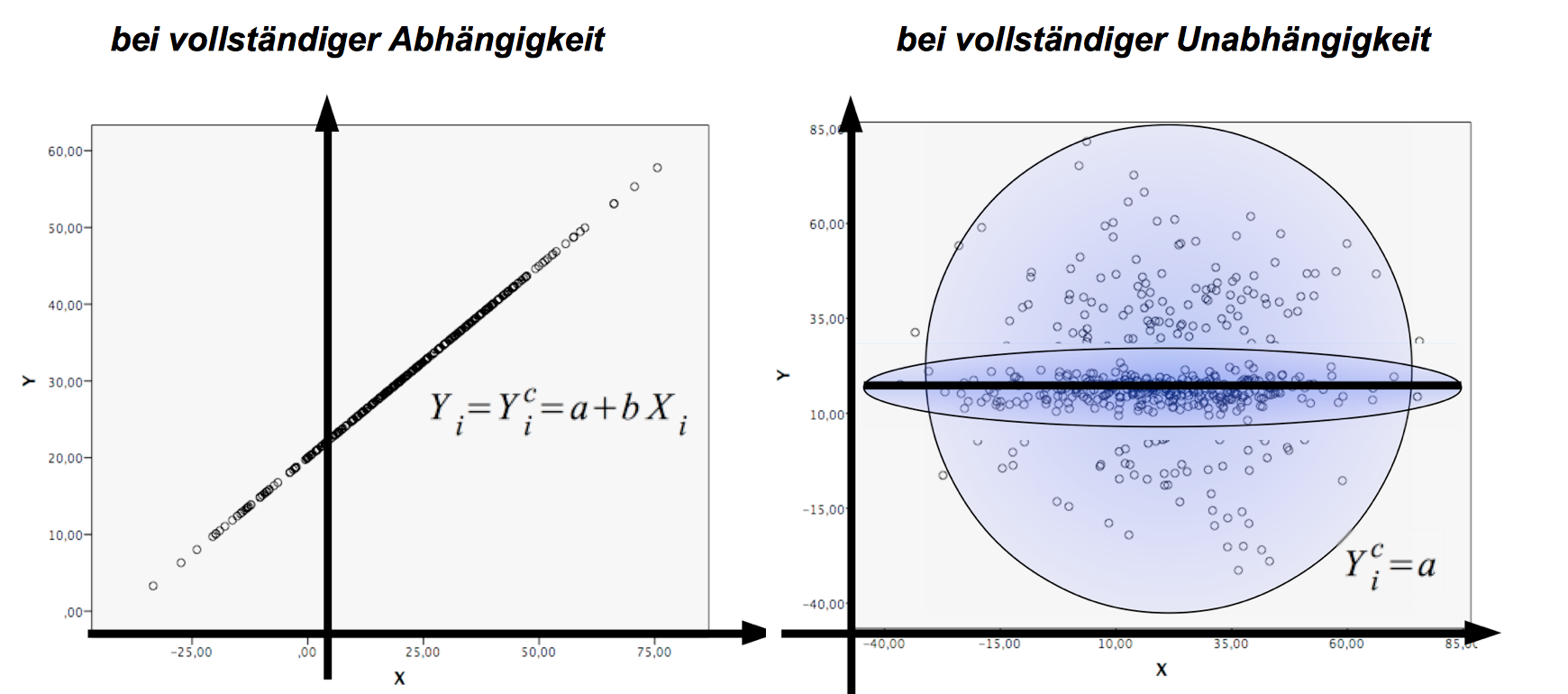
Bei vollständiger Abhängigkeit würden alle Punkte auf
einer (unsichtbaren) Geraden liegen und wir erhielten:
Y i = Yi c = a + b ·X i
Im Falle der Unabhängigkeit wäre die idealisierte Punktwolke
In diesen drei Fällen wäre die Regressionsfunktion eine Parallele zur X - Achse mit: Yi c = a = Ȳ
In der Realität ist nun eher ein Streuungsdiagramm mit einer mehr oder weniger ausgeprägten Streuung um eine Regressionslinie zu erwarten, deren Ausmaß mit einem Zusammenhangsmaß quantifiziert werden soll.
b) Die Anforderungen an ein Korrelationsmaß
Die gewünschten Eigenschaften des Maßes sowie die dominierenden Maße werden in folgendem Schaubild vorgestellt:
Schaubild 11-2: Kriterien für Korrelationsmodelle

Die gebräuchlichsten Maßzahlen,
um für metrische Daten die Stärke des Zusammenhanges zu
ermitteln sind der Korrelationskoeffizient r nach Bravais-Pearson und sein Quadrat der Determinationskoeffizient r2. Diese werden in den folgenden Abschnitten 2 und 3 abgeleitet.
2. Der Korrelationskoeffizient r
a) Das Konzept der Kovarianz
Die Kovarianz
(COV) war bereits Bestandteil der Formel für den
Regressionskoeffizienten b. Sie ist ein Ausdruck der gemeinsamen
Variation zweier Variablen und wie folgt definiert:
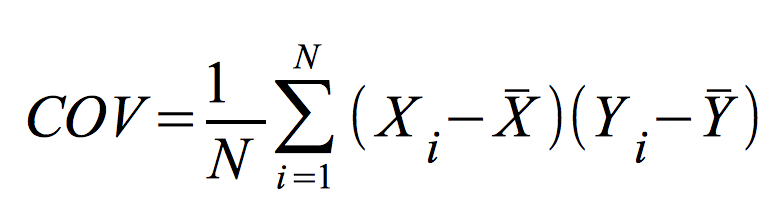
Das Konzept der Kovarianz setzt
nicht bei den originären Beobachtungen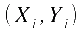 an,
sondern bei deren Abweichungen von ihren jeweiligen Mittelwerten,
also bei an,
sondern bei deren Abweichungen von ihren jeweiligen Mittelwerten,
also bei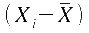 und und
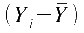 sowie
dem Produkt dieser beiden Abweichungen. sowie
dem Produkt dieser beiden Abweichungen.
Sind beide Abweichungen positiv oder beide negativ, ist das Produkt positiv.
Ist eine der Abweichungen positiv, die andere negativ, ist das Produkt negativ.
Das Vorzeichen der Kovarianz hängt dann davon ab, ob die positiven oder die negativen Komponenten überwiegen.
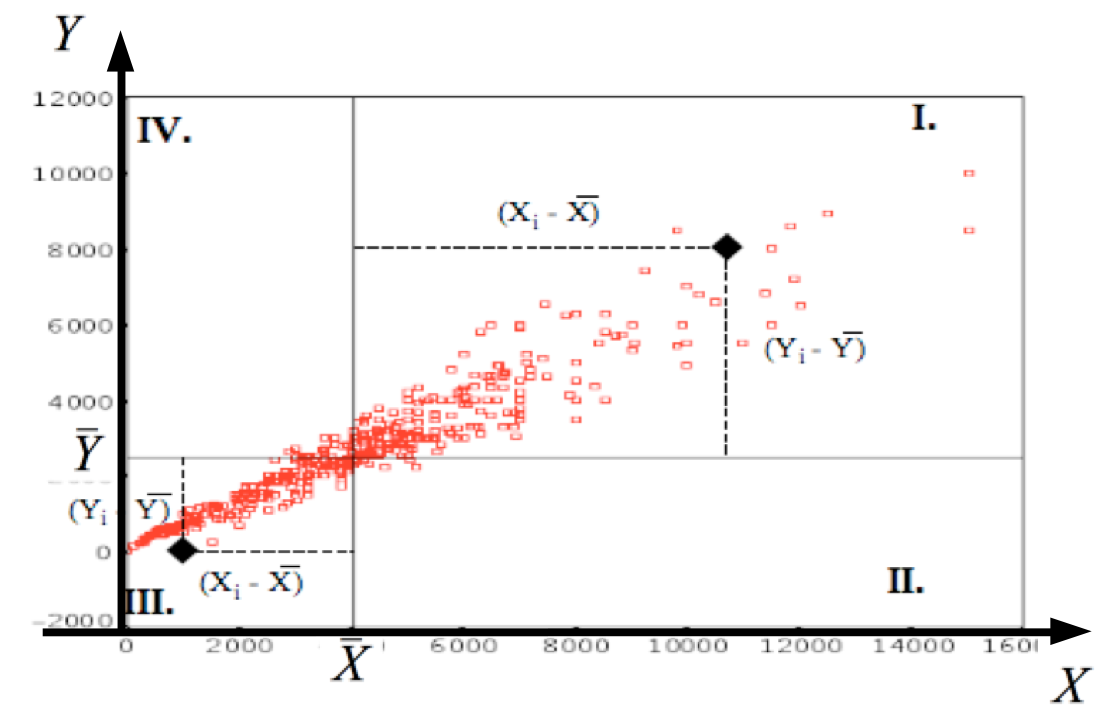
Bei einem gleichgerichteten
Zusammenhang liegen die Beobachtungen überwiegend im I. und III. Quadranten des Koordinatensystems (vgl. Abb. 11-10). Weil die Abweichungspaare überwiegend entweder beide positiv oder beide negativ sind, nimmt ihr Produkt und damit 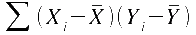 einen
positiven Wert an. einen
positiven Wert an.
Bei gegenläufigen Zusammenhängen finden sich die Beobachtungen vor allem im II. und IV. Quadranten.
Deshalb ergibt sich eine Häufung von Abweichungspaaren mit unterschiedlichem
Vorzeichen und damit eine insgesamt negative Kovarianz.
Bei einer
gleichmäßigen Streuung aller Wertepaare über alle vier Quadranten des
Koordinatensystems resultiert dem zu Folge eine Kovarianz von null.
Abbildung 11-10: Die Kovariation der Beobachtungen im Streuungsdiagramm
Da die Kovarianz mit dem Ausmaß der Streuung der Variablen wächst und deshalb den in Schaubild 11-2 formulierten Kriterien nicht genügt, muss sie um diese abträglichen Einflüsse bereinigt werden.
b) Der Korrelationskoeffizient nach Bravais-Pearson
Zur Berechnung des Koeffizienten wird deshalb die Kovarianz durch die
Standardabweichungen der beiden Variablen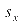 und und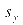 dividiert. dividiert.
Im allgemeine Fall gilt somit für den Korrelationskoeffizienten r:
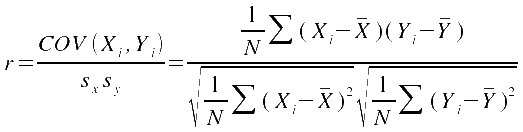
Für die
Berechnung von Hand und per Arbeitstabelle verwendet man wieder die
Umformungen:
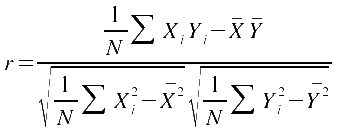
Für gruppierte Daten werden folgende Formeln zu Grunde gelegt:
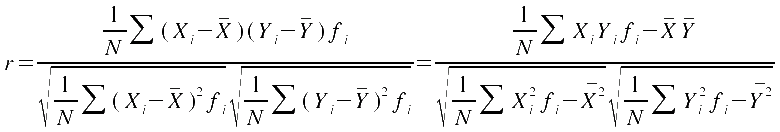
r liegt im
Wertebereich: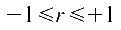 ,
wobei -1 einem vollständigen negativen, 0 der statistischen
Unabhängigkeit und +1 einem vollständigen positiven
Zusammenhang entspricht. ,
wobei -1 einem vollständigen negativen, 0 der statistischen
Unabhängigkeit und +1 einem vollständigen positiven
Zusammenhang entspricht.
c) Die rechnerische Beziehung zwischen Korrelationskoeffizient und Regressionskoeffizient
Der
Zähler der Berechnungsformel für b ist identisch mit dem
Zähler des Korrelationskoeffizienten r. Im Nenner von r steht das Produkt der beiden Standardabweichungen, im Nenner von b die Varianz von X.
Zwischen b und r besteht daher folgende Beziehung:
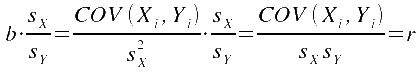 , ,
r ergibt sich somit auch über:
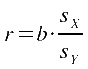
d) Die Korrelationszusammenhänge im Datensatz
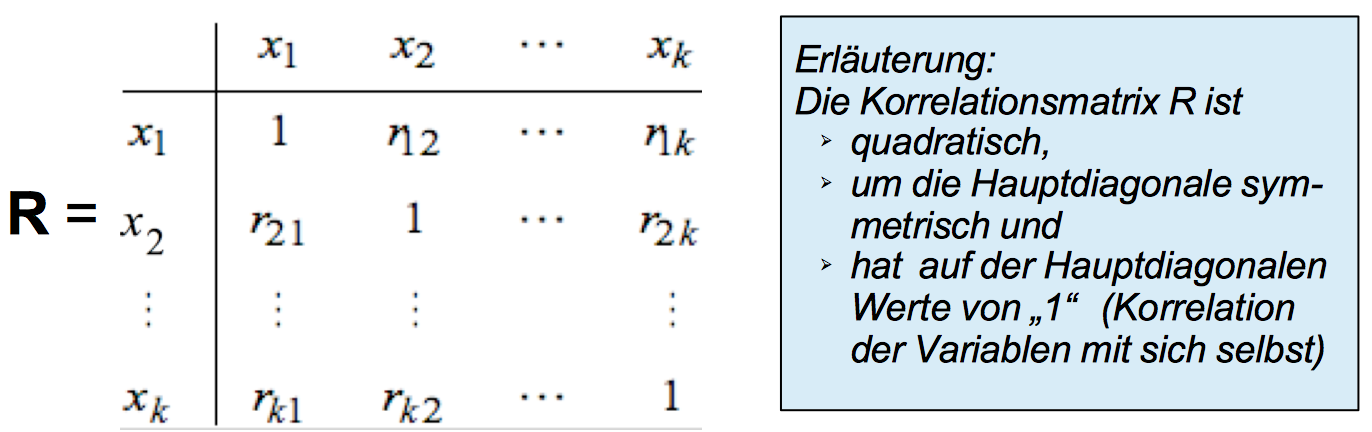
Oft ist es sinnvoll, sich einen Überblick über die Korrelationen zwischen den k Variablen eines Datensatzes zu verschaffen.
Diese lassen sich in einer sog. Korrelationsmatrix R zusammengefasst darstellen. Dabei definieren die k Variablen die Zeilen und Spalten der Matrix. In den Tabellenfeldern finden sich die Korrelationskoeffizienten ri,j (i,j = 1...k)
Abbildung 11-11: Die Korrelationsmatrix R
3. Der Determinationskoeffizient r2
Das Konzept des Determinationskoeffizienten
beruht auf dem Prinzip der Varianzzerlegung.
a) Die Komponenten der Gesamtvarianz
Die Streuung der Beobachtungen der abhängigen Variablen um ihren Durchschnitt wird durch Gesamtvarianz der Yi (i = 1...N) ausgedrückt:
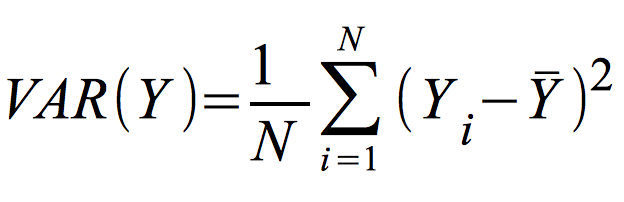
Die Gesamtvarianz ergibt sich aus den Abweichungen der Yi vom arithmetischen Mittel
Ȳ (vgl. Abb. 11-12).
Abbildung 11-12: Die Gesamtvarianz der abhängigen Variablen Yi
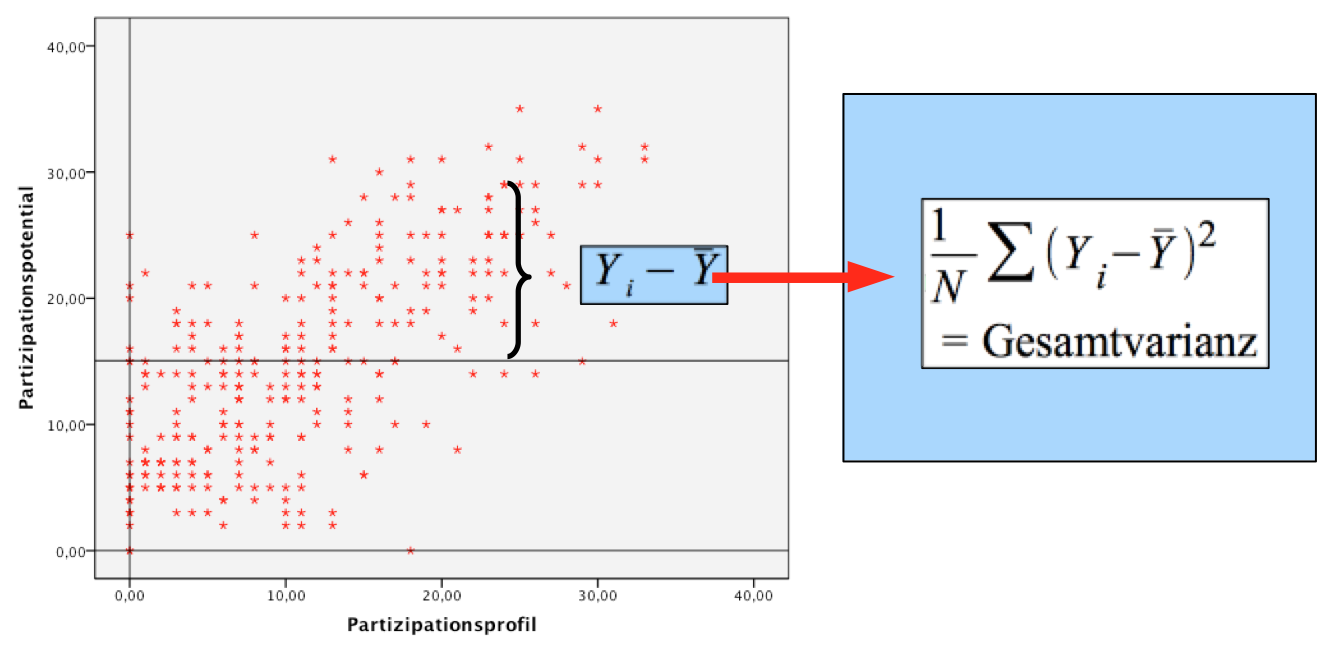
Diese Varianz wird in zwei Komponenten aufgeteilt:
Die erste Komponente erfasst die "erklärte Varianz". Sie ergibt sich aus den Abweichungen der Werte der Regressionsfunktion Yi c vom arithmetischen Mittel
Ȳ (vgl. Abb. 11-13).
Abbildung 11-13: Die erklärte Varianz der abhängigen Variablen Yi
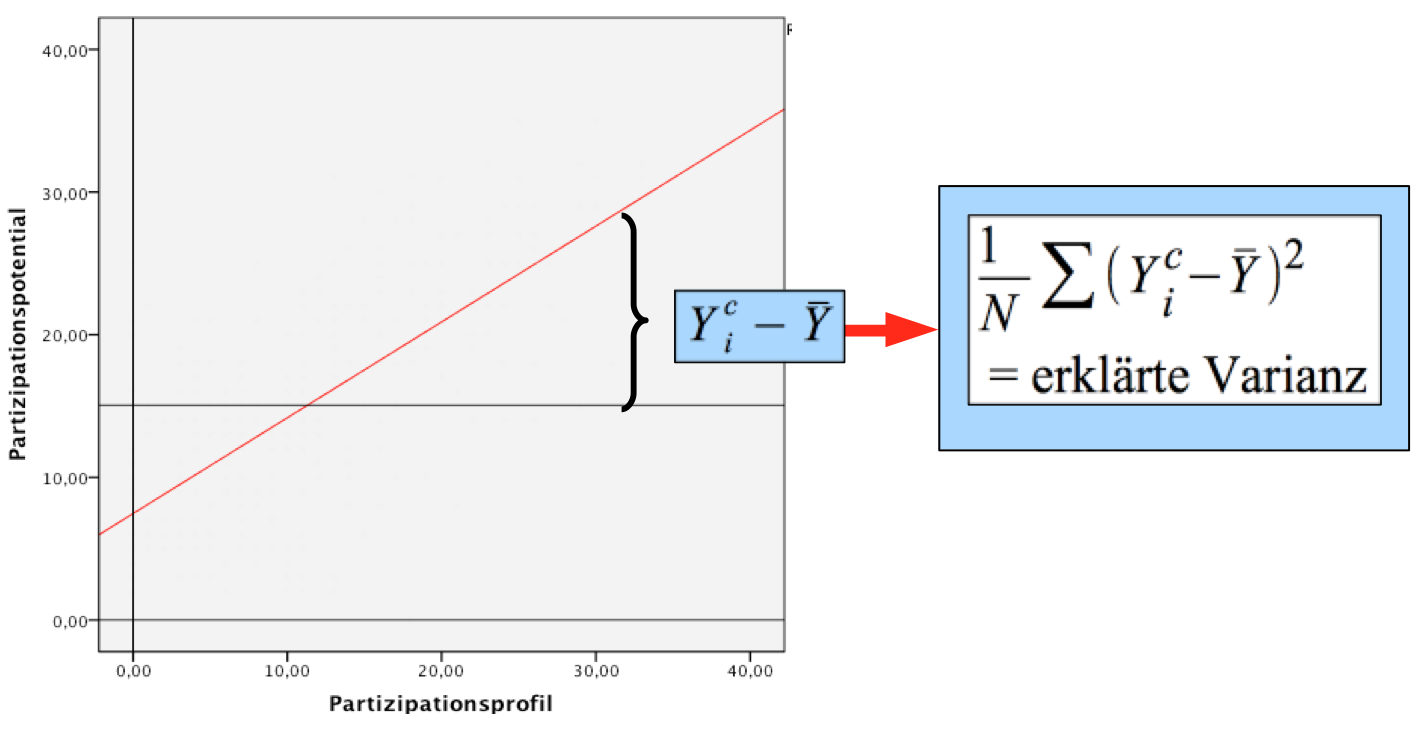
Die zweite Komponente, die "nicht-erklärte Varianz" oder "Fehler-Varianz" gibt den Zufallseinfluss wieder.
Diese ergibt sich aus den Abweichungen der Beobachtungen Yi von der Regressionsfunktion Yi c (vgl. Abb. 11-14)
Abbildung 11-14: Die nicht-erklärte Varianz der abhängigen Variablen Yi
b) Die Varianzzerlegung
Die unter a) definierten Komponenten "erklärte Varianz" und "nicht-erklärte Varianz" schöpfen die Gesamtvarianz vollständig aus. Dies soll im Folgenden demonstriert werden.
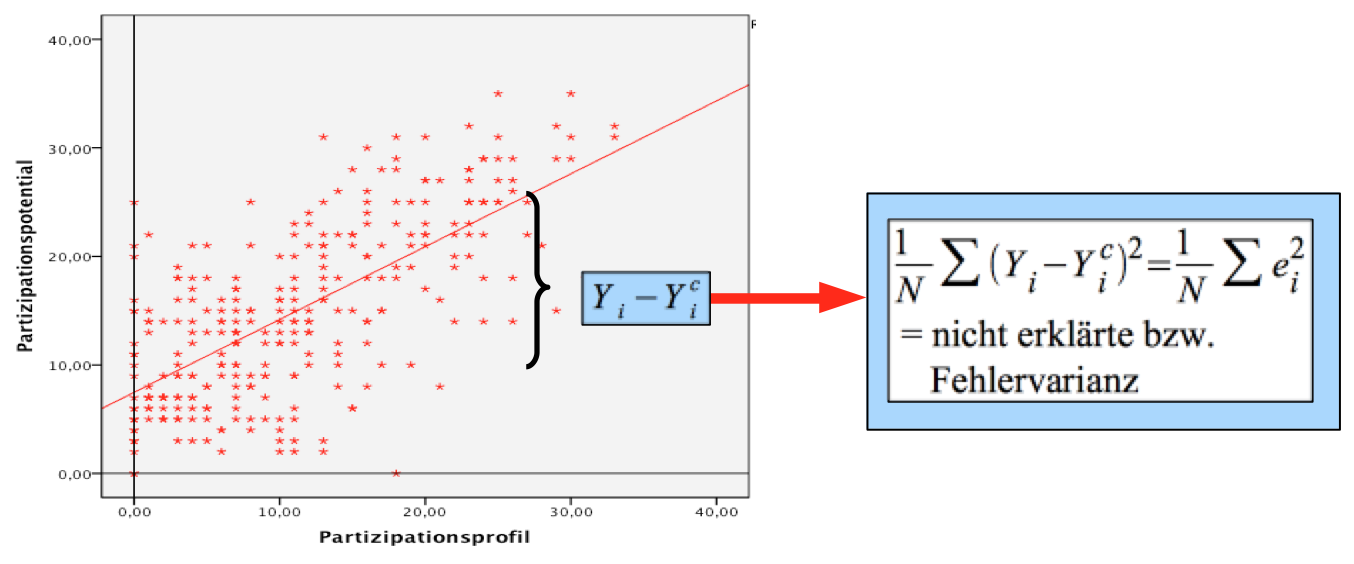
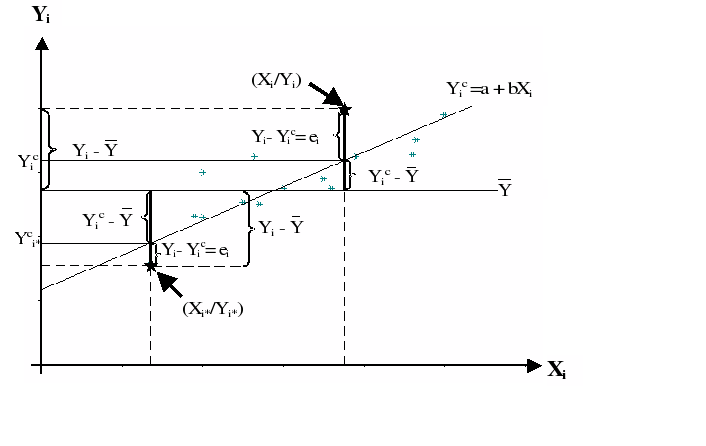
Die graphische Veranschaulichung
Betrachten wir dazu zuerst die Abweichungen der Beobachtungen Yi von ihrem Mittelwert Ȳ. Diese Abweichungen Yi
- Ȳ lassen sich, wie in Abb. 11-15 gezeigt, in eine erklärte (Yi c
- Ȳ) und in eine nicht-erklärte Abweichung (Yi - Yi c) aufspalten
Abbildung 11-15: Zerlegung
der Gesamtabweichungen Yi
- Ȳ
Die rechnerische Ableitung
Ausgehend von der Zerlegung der Abweichungen in Abb. 11-15 soll dies für die Varianz an Hand des folgenden Schaubildes demonstriert werden.
Abbildung 11-16: Zerlegung
der Gesamtvarianz in drei Schritten

Zu 1): Die Zerlegung der Gesamt-Abweichungen Yi - Ȳ in einen erklärten und in einen nicht erklärten Teil gilt, weil die rechte Seite der Gleichung nur um ± Yi c erweitert wurde.
Zu 2): Die Zerlegung der Summe der Abstandsquadrate ergibt sich aus 1) durch Quadrierung und Aufsummierung der Quadrate für alle Beobachtungen.
Zu 3): Die Zerlegung der Varianz resultiert aus der Division der Gleichung 2) durch N.
c) Die Formel für den Determinationskoeffizienten r2
Der Determinationskoeffizient r2 ist , wie der Begriff nahe legt, das Quadrat des Korrelationskoeffizienten nach Bravais-Pearson mit:
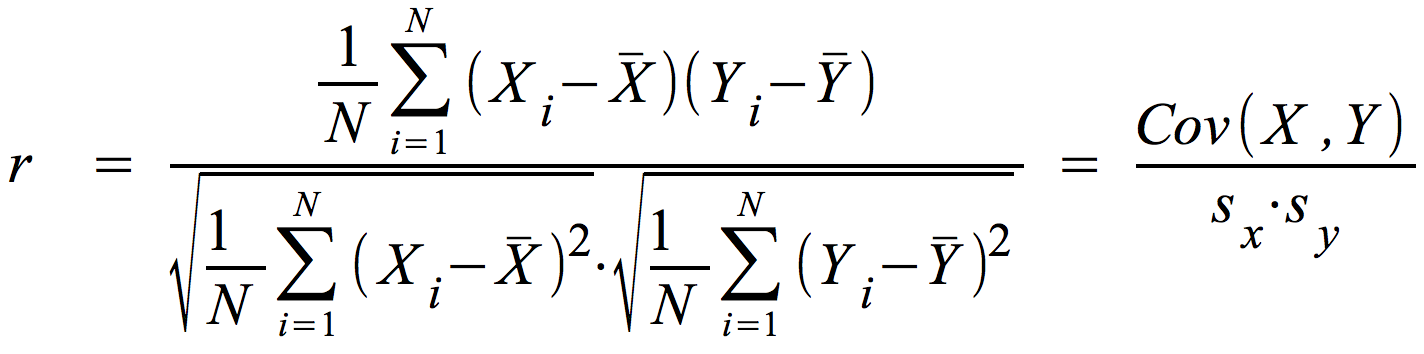
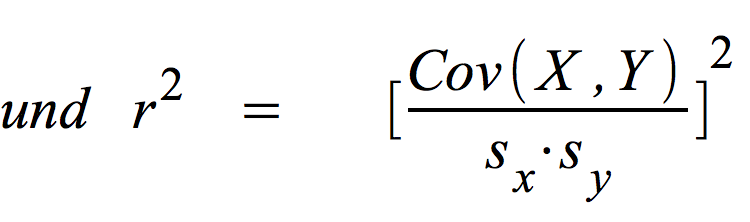
Die Varianzzerlegung liefert nun die Grundlage einer alternativen Definition eines Zusammenhangmaßes. Dazu wird das Verhältnis der erklärten Varianz zur Gesamtvarianz gebildet.
Diese Verhältnis hat die für ein Zusammenhangsmaß günstigen Eigenschaften:
Das Maß wird "0", wenn sich die Regressionsgerade als Parallele zur X-Achse ergibt. Dann ist Gesamtvarianz identisch ist mit der Fehlervarianz und die erklärte Varianz ist "0".
Das Maß wird "1", wenn sich alle Beobachtungen auf der Regressionsgeraden befinden. Dann ist Gesamtvarianz identisch ist mit der erklärte Varianz und die Fehlervarianz ist "0".
Es lässt sich nun zeigen, dass das Verhältnis von erklärter Varianz zur Gesamtvarianz identisch ist mit r2.
Es gilt also:

4. Die praktische Arbeit mit r und r2
a) Die Berechnung der Koeffizienten
Zur Berechnung der Koeffizienten bezieht man sich am einfachsten auf die Formel für r und quadriert für r2 den darüber ermittelten Wert.
Da man in der Regel die
Regressionsfunktion schon berechnet hat und  und und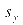 meist bekannt sind, kann b zur einfacheren Berechnung von r übernommen
werden. r ergibt sich somit auch über: meist bekannt sind, kann b zur einfacheren Berechnung von r übernommen
werden. r ergibt sich somit auch über:
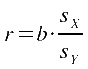
Konkret erhalten wir für den Zusammenhang zwischen tatsächlicher und gewünschter Beteiligung, für den in XI-I die Regressionsfunktion bestimmt wurde, die folgenden Werte

b) Die Interpretationen der Zusammenhangsmaße
Die Interpretation von r und r2 zielt darauf ab, Aussagen über die Stärke des Zusammenhangs zu machen. Diese stützen sich auf die jeweiligen Definitionen der Koeffizienten. Wegen der unterschiedlichen Wertebereiche können sie sich durchaus unterscheiden:
Die Interpretation von r
Dabei sind zwei Aspekte zu unterscheiden: Das Vorzeichen und der Wert.
-
Das Vorzeichen charakterisiert die Richtung des Zusammenhangs:
- Ein negatives Vorzeichen steht für einen umgekehrt proportionalen Zusammenhang.
- Ein positives signalisiert einen gleichgerichteten Zusammenhang.
-
Bezüglich der Aussage von r zur Stärke des Zusammenhangs finden sich in der Literatur durchaus unterschiedliche Vorschläge. Ordnet man den Intensitäten gleich große Wertebereiche zu, resultiert die folgende Einteilung:
Abbildung 11-17: Wertebereiche für r

-
In unserem Beispiel besteht demnach bei einem Wert von r = 0,69 ein hoher Zusammenhang zwischen der gewünschten und der tatsächlichen Beteiligung an betrieblichen Entscheidungsprozessen.
Die Interpretation des Determinationskoeffizienten
Bei der Interpretation des Determinationskoeffizienten greift man auf das Verhältnis von erklärter zur Gesamtvarianz zurück. Damit drückt der Koeffizient die Stärke eines Zusammenhangs linear zwischen 0% und 100% aus.
So bedeutet ein r2 von 0,476, dass die Varianz der unabhängigen Variablen Partizipationsprofil 47,6% der Varianz der abhängigen Variablen Partizipationspotential erklärt. Dieser Wert erreicht also knapp die Hälfte des Wertebereichs und liegt damit eher im mittleren Bereich.
Die Interpretationen im Vergleich
Beide Vorzeichen unterscheiden sich bei negativen Zusammenhängen hinsichtlich des Vorzeichens. Da diese Unterscheidung bei r2 durch die Quadrierung verloren geht, sind beide Koeffizienten bei Aussagen zum Zusammenhang heranzuziehen.
Da in einfachen linearen Zusammenhängen eine mehr oder weniger große Anzahl von weiteren, Einfluss nehmenden Variablen ausser Acht bleibt, kann nur in seltenen Fällen davon ausgegangen werden, dass eine unabhängige Variable die Varianz der abhängigen Variablen wesentlich erklärt.
Deshalb ist es sinnvoll sich bezüglich der Stärke des Zusammenhangs auf r zu beziehen und zusätzlich mit r2 das Ausmaß der erklärten Varianz zu betonen.
Darüber hinaus ist festzuhalten, dass die Stärke eines Zusammenhangs nicht unabhängig vom untersuchten Sachverhalt bestimmt werden kann.
In Fällen wie dem hier exemplarisch behandelten betrieblichen Entscheidungsprozess, auf den Status, Ausbildung und Geschlecht ebenfalls Einfluss nehmen, kann ein Ergebnis von r = 0,69 durchaus als starker Zusammenhang bezeichnet werden, auch wenn nur knapp die Hälfte der Varianz des Partizipationspotentials durch das Profil erklärt wird.
Schließlich ist noch auf die in ViLeS 2 behandelten induktiven Aspekte hinzuweisen, wo die Frage der Stärke des Zusammenhangs überlagert wird von der Frage, ob der in der Untersuchung festgestellte Zusammenhang signifikant ist, d.h. auch für die der Untersuchung zugrunde liegende Grundgesamtheit der Objekte gilt.
Dabei stellt sich oft heraus, dass Ergebnisse, die auf mittlere bis höhere Einflüsse hinweisen, mangels ausreichender Fallzahlen nicht signifikant sind und andererseits durchaus auch sehr niedrige Werte von r bei hohen Fallzahlen einen gesicherten Zusammenhang belegen.
|



