 |
Konzepte und Definitionen im Modul XI-1 Das einfache lineare Regressionsmodell
1. Tabellarische und graphische Aufbereitung zweidimensionaler Daten
a) Tabellarische und rechnerische Vorarbeiten
b) Das Konzept des Streuungsdiagramms
Im Beispiel greifen wir auf die metrischen Ursprungswerte der Variablen Partizipationsprofil und Partizipationspotential aus der Partizipationsuntersuchung zurück, um den Zusammenhang zwischen beiden Variablen graphisch darzustellen und hinsichtlich seiner Richtung und Stärke zu analysieren.
Das Koordinatensystem
Die Darstellung der Beobachtungen einer zweidimensionalen Häufigkeitsverteilung in einer Punktwolke schöpft die im Datensatz vorhandenen Informationen vollständig aus, da sie jedes Wertepaar in Form eines Punktes im Koordinatensystem abbildet.
In einem ersten Schritt müssen die X- und die Y-Koordinaten festgelegt werden. Da nicht davon auszugehen ist, dass die tatsächliche Beteiligung von den Wünschen abhängt sondern umgekehrt diese weckt, werden das Partizipationsprofil auf der X-Achse und das Partizipationspotentiel auf der Y-Achse abgetragen.
Das Streuungsdiagramm
Abbildung 11-1: Streuungsdiagramm zur tatsächlichen und zur gewünschten Partizipation
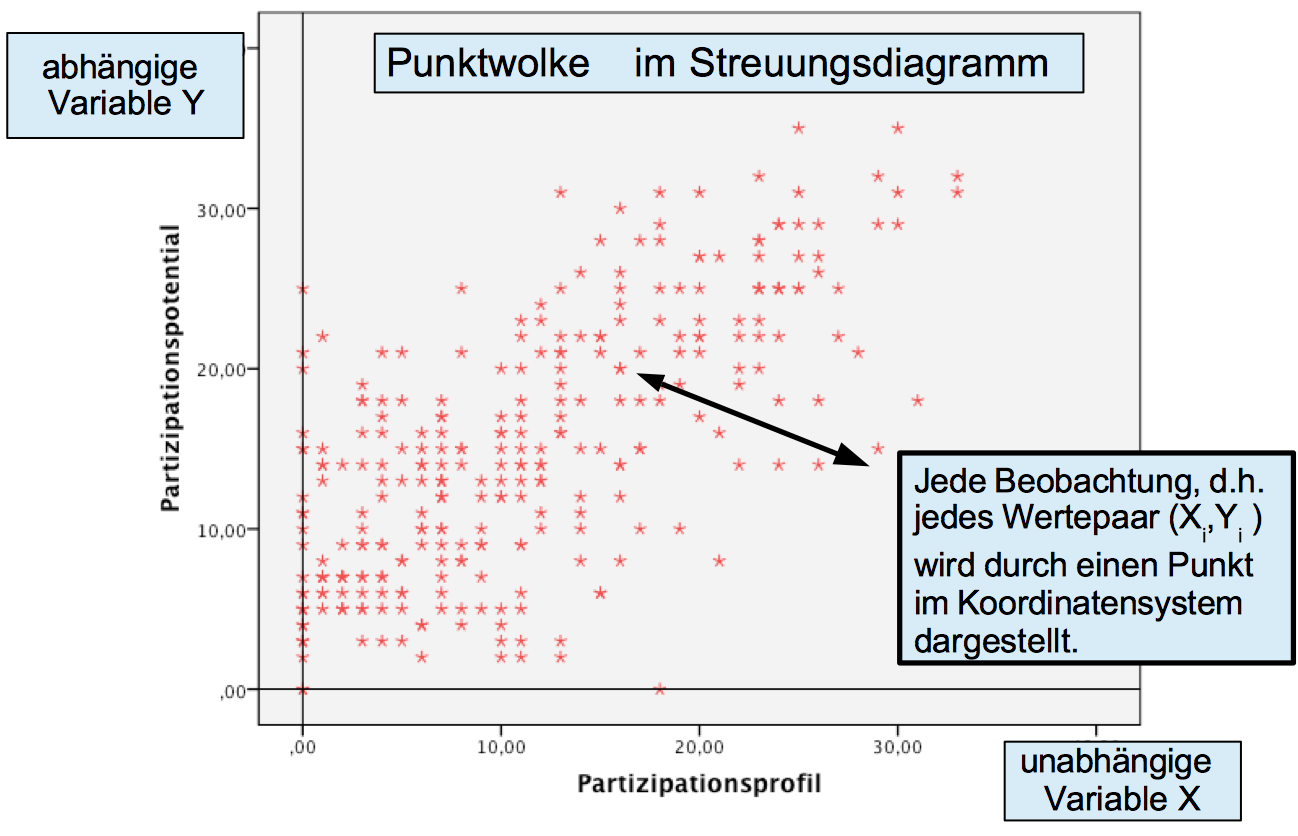
Die Punktwolke signalisiert:
einen positiven, linearen Zusammenhang zwischen den Variablen, d.h. dass sich die beiden Variablen gleichsinnig und im Durchschnitt etwa proportional verändern und
dass dieser Zusammenhang deutlich von Zufallseinflüssen beeinträchtigt ist, ansonsten lägen alle Beobachtungen auf einer Geraden.
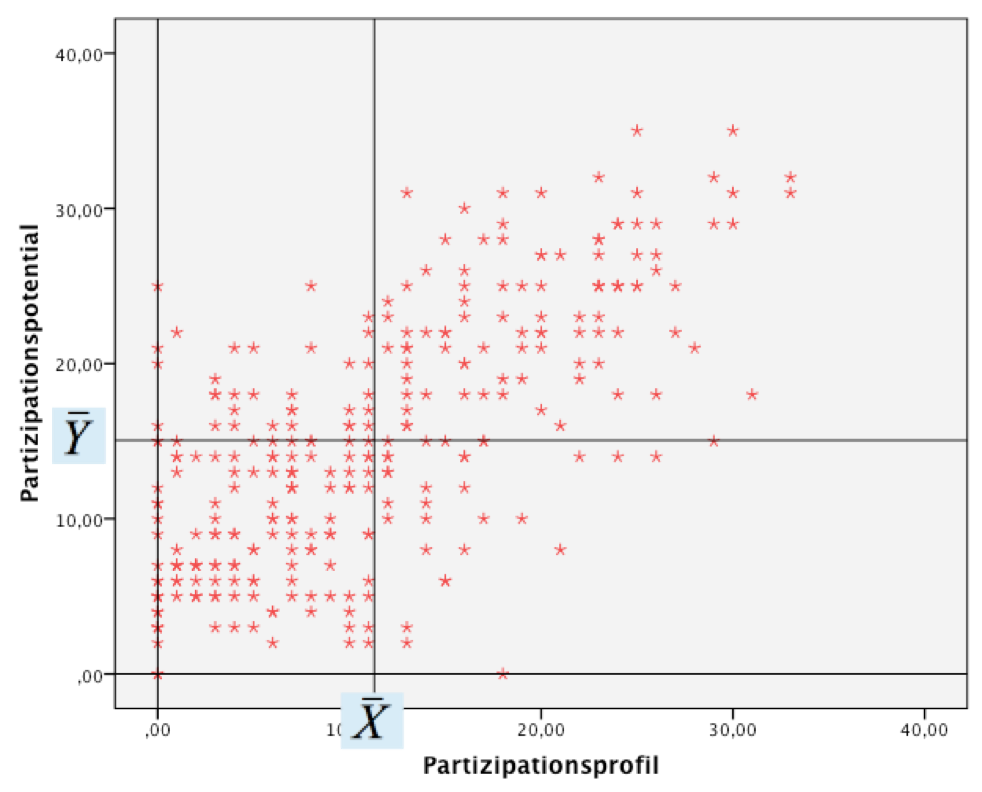
Wie in Abb. 11-2 ersichtlich, hat das Zentrum der Punktwolke die Koordinaten (X̄ , Ȳ).
Abbildung 11-2: Lage der Punktwolke
2. Die Ermittlung der linearen Regressionsfunktion
a) Das Konzept der linearen Regressionsfunktion
Bei der einfachen linearen Regression gehen
wir davon aus, dass es nur eine abhängige und eine unabhängige
Variable gibt. Zudem unterstellen wir einen linearen Zusammenhang
zwischen den Variablen. Die unabhängige
Variable wird mit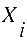 ,
die abhängige Variable wird mit ,
die abhängige Variable wird mit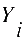 bezeichnet
(I=1...N). bezeichnet
(I=1...N).
Damit lässt sich die abhängige
Variable als lineare Funktion der unabhängigen Variablen in Form
der folgenden Geradengleichung darstellen.
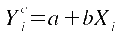
In ihr ist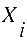 ein
konkreter, beobachteter Wert der unabhängigen Variablen ein
konkreter, beobachteter Wert der unabhängigen Variablen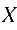 . .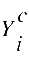 ist
der Wert, den die abhängige Variable annähme, wenn die
unabhängige Variable den Wert ist
der Wert, den die abhängige Variable annähme, wenn die
unabhängige Variable den Wert aufweist
und keine weiteren Einflüsse auf aufweist
und keine weiteren Einflüsse auf einwirken würden. einwirken würden.
b gibt
die Steigung der Geraden und a ihren
Achsenabschnitt an. Eine negative Steigung, d. h. ein negatives
Vorzeichen vor b bedeutet
einen negativen Zusammenhang, eine positive Steigung einen positiven
Zusammenhang.
Vorab wurde bereits geklärt, welche
Variable die abhängige und welche die unabhängige ist.
b) Die Positionierung der linearen Regressionsfunktion in der Punktwolke
Die Hypothese eines linearen Zusammenhangs muss nun in Übereinstimmung mit den in der Punktwolke manifestierten Daten gebracht werden, d.h. die Regressionsfunktion muss optimal, etwa wie in Abb. 11-3 dargestellt, in die Punktwolke eingepasst werden:
Abbildung 11-3: Lage der der Regressionsfunktion in der Punktwolke
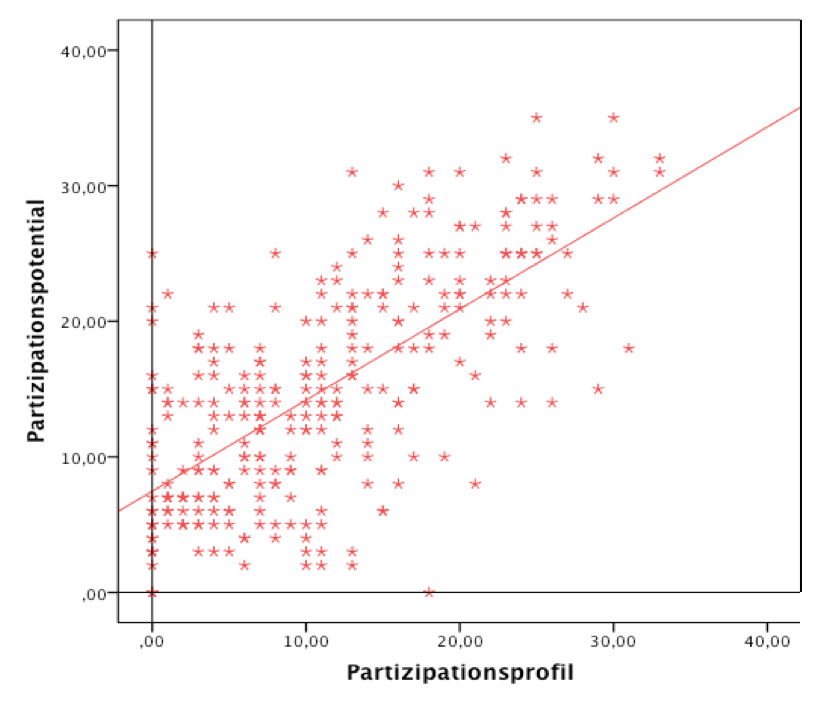
Wie man in Abb. 11-3 sieht, folgen die Beobachtungen nicht unmittelbar einer
mathematischen Funktion sondern nur tendenziell. Sie streuen so zu
sagen um eine optimale Linie, die in unserem Fall durch eine
Geradengleichung zu beschreiben ist.
Man könnte dieses Optimum dadurch erreichen, dass man die Gerade solange verschiebt, bis der optische Eindruck die beste Einpassung ergibt. Im nächsten Schritt wird allerdings mit der "Methode der kleinsten Quadrate eine mathematische Lösung des Problems vorgestellt.
c) Die Methode der kleinsten Quadrate
Um für die beiden Parameter der Geradengleichung,
die Steigung b und den Achsenabschnitt a adäquate Formeln zu definieren, wird die gesuchte Funktion über
ein mathematisches Minimierungskalkül bestimmt. Die Logik des
Modell erschließt sich relativ einfach über die graphische
Darstellung in Abb. 11-4:
Abbildung
11-4: Punktwolke und lineare Regressionsfunktion
Die Abweichungen
der Beobachtungen in der abhängigen Variablen von
der linearen Funktion werden als Fehler von
der linearen Funktion werden als Fehler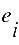 bezeichnet. bezeichnet.
Diese sind einmal dadurch bedingt, dass es - anders als in
beobachtbaren naturwissenschaftlichen Zusammenhängen – in
sozialen und ökonomischen Bezügen keinen Determinismus gibt.
Neben dem Zufall sind bei der Fehlerbetrachtung im einfachen linearen
Regressionsmodell meist noch weitere unabhängige Variablen in Rechnung zu
stellen, die in die Fehlergröße eingehen.
Damit ergeben sich
die Beobachtungen in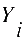 additiv
aus einem funktionalen Zusammenhang additiv
aus einem funktionalen Zusammenhang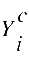 und
einem nicht weiter aufgeschlüsselten
„Fehlerterm“ und
einem nicht weiter aufgeschlüsselten
„Fehlerterm“ 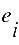 : :
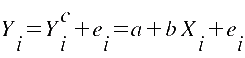
Man versucht nun, die Gerade so durch die
Punktwolke zu legen, dass die Fehler insgesamt minimiert werden. Weil die
Summe der einfachen Abstände Null ergibt, soll die Summe der quadrierten
Abstände der Beobachtungen von der Geraden ein Minimum
aller denkbaren Geraden annehmen.
d) Die Formeln für die Parameter der Regressionsfunktion
Die Methode der
kleinsten Quadrate besteht nun in der Lösung folgender mathematischer Zielfunktion:
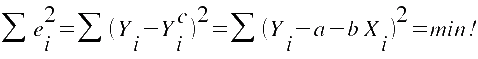
Dazu wird
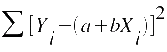 partiell
nach a und b differenziert. Die partiellen Differentiale werden null
gesetzt und nach den Parametern a und b aufgelöst. Die 2.
Ableitungen sollten dabei negativ sein. partiell
nach a und b differenziert. Die partiellen Differentiale werden null
gesetzt und nach den Parametern a und b aufgelöst. Die 2.
Ableitungen sollten dabei negativ sein.
Abbildung 11-5:
Ableitung der Regressionsparameter
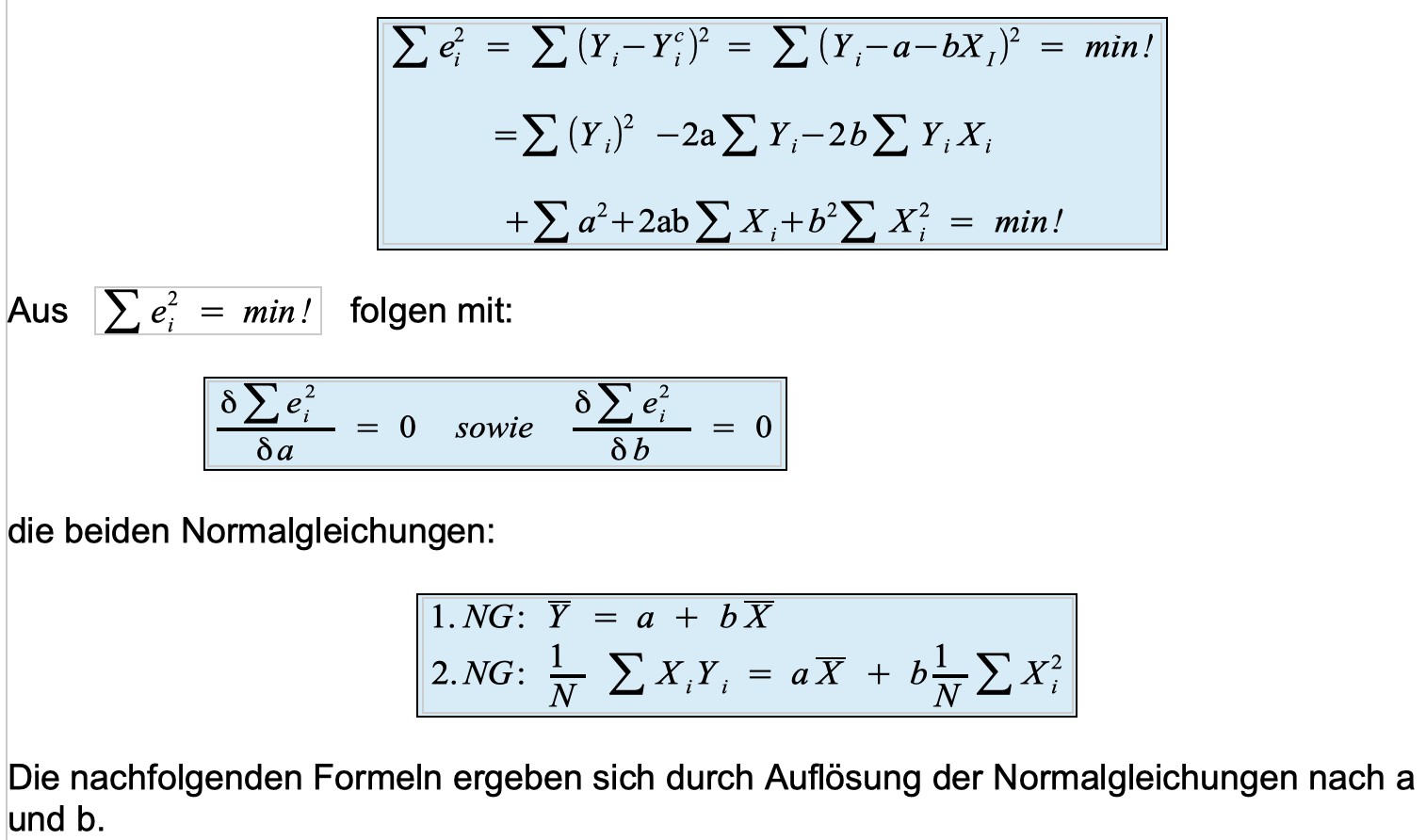
Aus den Normalgleichungen wird zunächst die Steigung b bestimmt (zur genaueren Herleitung vgl. Litz, 2003 S. 162 ff).
Die Formel für den Regressionskoeffizienten b
lautet für Einzelwerte:
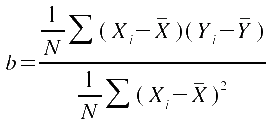 =
=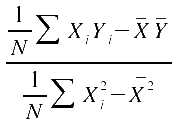 bzw.: bzw.:
lautet für
gruppierte Daten:
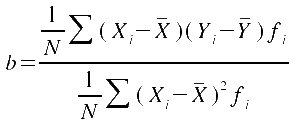 = =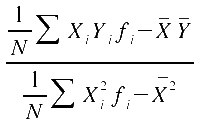 . .
Die zweite Schreibweise ergibt
sich durch Umformung und führt zu Ausdrücken, die sich über
eine Arbeitstabelle berechnen lassen (vgl. den nachfolgenden Teil "Beispiele und Aufgaben").
b lässt
sich auch als Verhältnis der Kovarianz von X und Y zur Varianz
von X darstellen: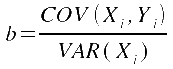 ,
wobei die Kovarianz der numerische Ausdruck der gemeinsamen Variation
von X und Y ist (vgl. dazu Näheres in Kap.XI-2). ,
wobei die Kovarianz der numerische Ausdruck der gemeinsamen Variation
von X und Y ist (vgl. dazu Näheres in Kap.XI-2).
Die Formel für die Regressionskonstante a
Aus den kleinsten Quadraten
lässt sich die sogenannte Mittelpunktsgleichung ableiten,
die besagt, dass die Regressionsfunktion durch den Mittelpunkt der
Punktwolke geht (vgl. Abb. 11-6):
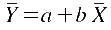
a ergibt sich am einfachsten
durch Einsetzen in diese Beziehung:
Die Regressionsfunktion
Damit ist die
Regressionsgerade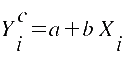 ermittelt. ermittelt.
3. Präsentation und Interpretation der Ergebnisse
Abbildung 11-6: Lage der der Regressionsfunktion in der Punktwolke
Zur Bewertung des Ergebnisses ist ein Vergleich der ermittelten Regressionsfunktion mit der 45°-Linie aufschlussreich. Diese beschreibt die Situation, in der tatsächliche Beteiligung und gewünschte Beteiligung identisch sind.
Abbildung 11-7: Regressionsfunktion und 45°- Linie
|



