Beispiele und Aufgaben im Modul X-3 Der Rangkorrelationskoeffizient nach Spearman
1. Das Beispiel
a) Die Ausgangstabelle und die Rangdifferenzen
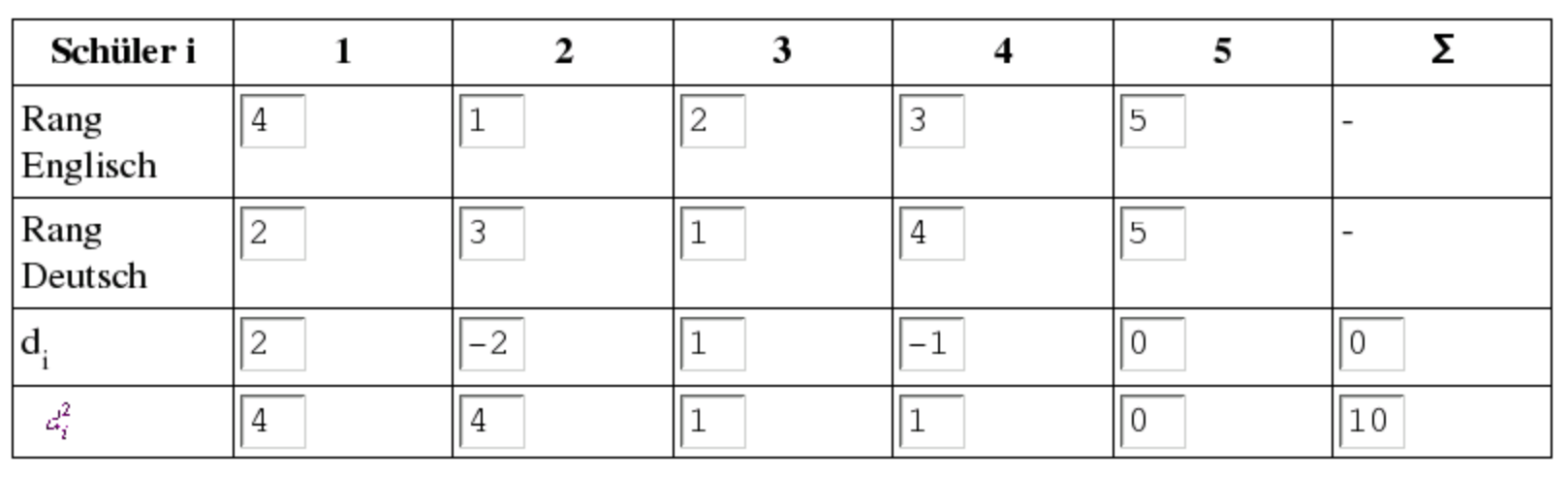
Ausgangspunkt des Rechenbeispiels sind die Rangunterschiede und Rangdifferenzen in den Fächern Deutsch und Englisch aus Tab. 10-5.
Tabelle 10-5: Bestimmung der Rangdifferenzen
b) Die Berechnung des Rangkorrelationskoeffizient nach Spearman
rs ergibt sich aus folgender Berechnung:
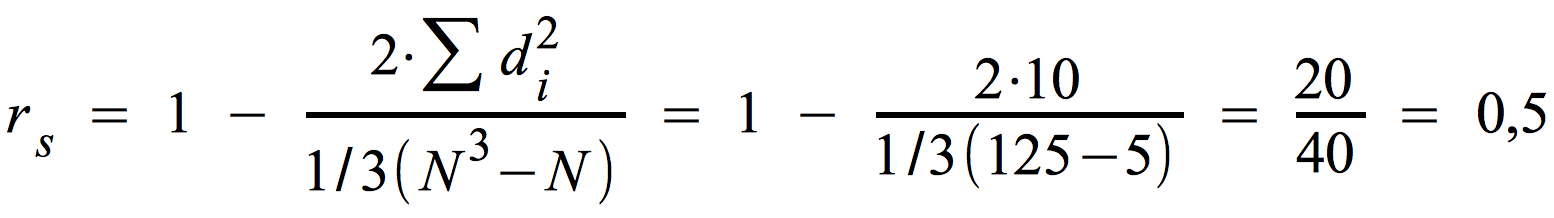
c) Die Interpretation des Ergebnisses
Die Voraussetzungen für die Verwendung des Rangkorrelationskoeffizienten sind gegegeben, wenn wir eine Äquidistanz zwischen den ordinalen Schülerleistungen unterstellen.
Mit einem Wert von rs = 0,5 können wir danach einen mittleren Zusammenhang konstatieren.
Im Vergleich zum unter X-1 berechneten Konkordanzmaß τa erhielten wir mit τa = 0,4 einen leicht geringeren Wert.
2. Die Aufgabe
a) Die Ausgangstabelle
Für die in X_1, "Beispiele und Aufgaben" in Tab. 10-2 vorgestellte Untersuchung zu unterschiedlichen Ansätzen einer Materialprüfung von Textilien haben sich die folgenden Rangreihen ergegeben:
Tabelle 10-6: Rangreihen bei der Materialprüfung

b) Die Aufgabenstellung
Berechnen Sie den Rangkorrelationskoeffizienten für die
und diskutieren Sie das Ergebnis,
auch in Bezug auf die Anwendbarkeit des
Rangkorrelationskoeffizienten.
c) Ein Tool zur Berechnung des Rangkorrelationskoeffzienten
Anhand der folgenden Anwendung können Sie die Berechnung des
Rangkorrelationskoeffizienten mit den obigen oder beliebigen Werten üben.
Wenn
Sie weniger als 7 Fälle verwenden möchten, geben Sie in den
Feldern einfach eine Null ein. Vergessen Sie in diesem Fall nicht, N
zu ändern.
Geben Sie die Rangdaten in die folgende Tabelle ein.
Interpretieren Sie Ihre Ergebnisse für die beiden Rangvergleich und vergleichen Sie diese mit den unter X-1 erzielten Konkordanzmaßen.
d) Varianten der Aufgabenstellung
Konstruieren Sie einen Fall, für den sich ein maximaler
positiver bzw. ein maximaler negativer Zusammenhang ergibt.
Wählen
Sie dabei N < 8 und geben Sie die Werte in das obige Tool ein..
e) Beantwortung von Fragen zur Rangkorrelation
Als weiter Aufgabe Beantworten Sie bitte folgende Fragen (wie immer mit "j"
oder "n"):
| 


