 |
Konzepte und Definitionen im Modul X-3 Der Rangkorrelationskoeffizient nach Spearman
1. Das Modell der Rangkorrelation
a) Das Konzept der Rangdifferenz
Der Rangkorrelationskoeffizient rs nach Spearman basiert auf der Bildung von Rangdifferenzen di, die für die n Merkmalsträger aus ihren jeweiligen Rangplätzen gebildet werden können:
-
Betrachtet werden die Rangunterschiede von Schülern in den Fächern Deutsch und Englisch aus Tab. 10-1, für die in Tab. 10-5 die Rangdifferenzen
di = Xi - Yi für i = 1 ....5 .
ermittelt werden.
Tabelle 10-5: Bestimmung der Rangdifferenzen
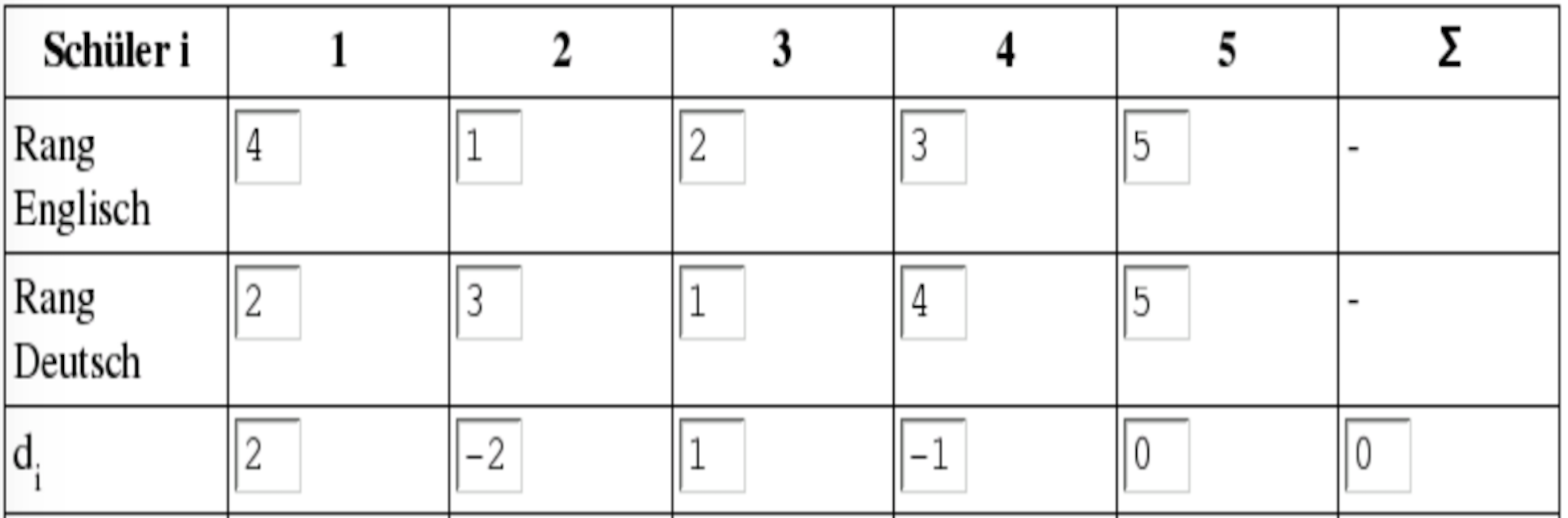
-
Die Ränge und die Rangdifferenzen werden in Abb. 10-2 veranschaulicht.
Abbildung 10-2: Rangdifferenzen im Schülervergleich
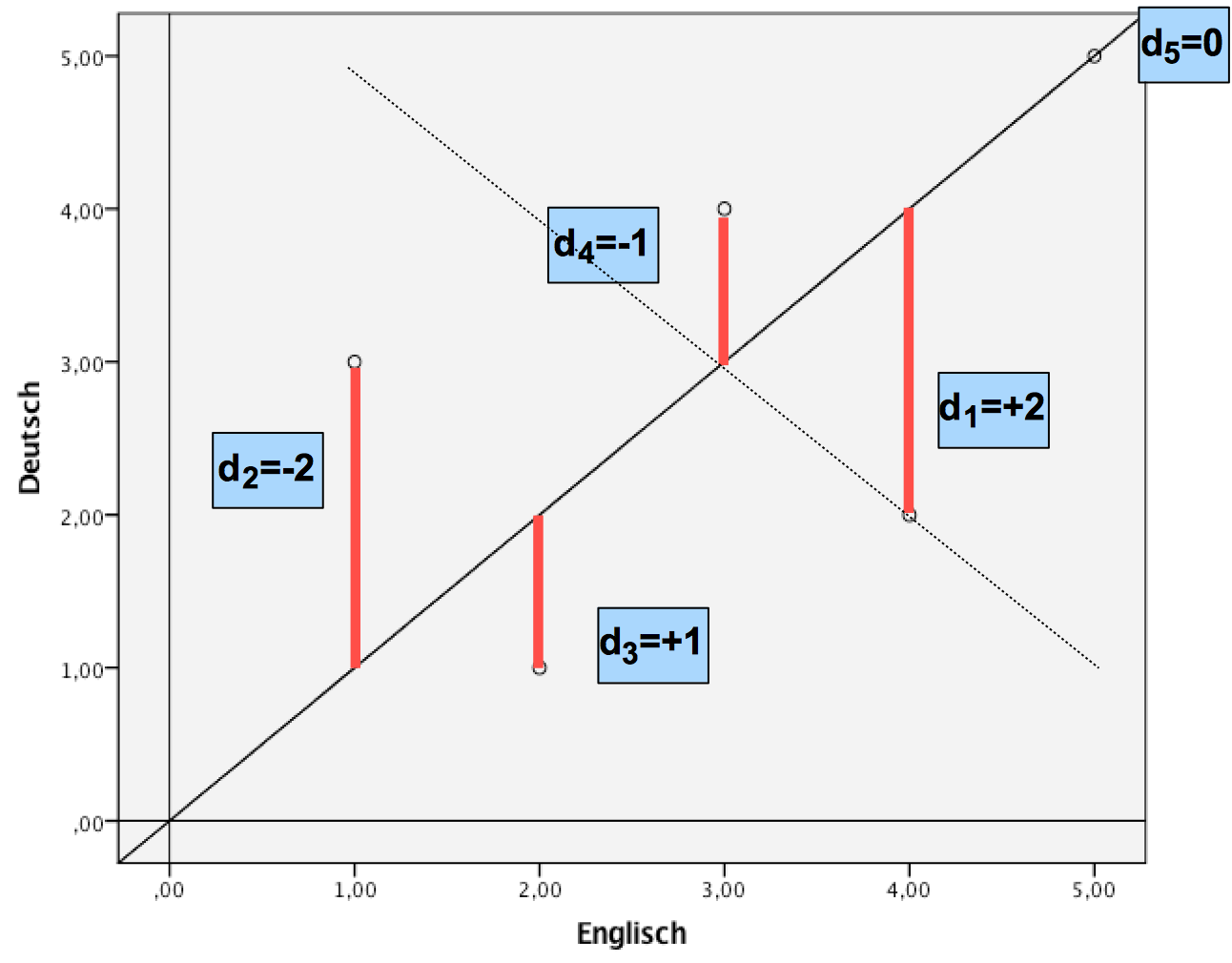
b) Die Konstruktion des Rangkorrelationskoeffizienten
Die Konstruktion des Koeffizienten basiert auf dem Ausmaß dieser Rangdifferenzen.
Die Rangdifferenzen sind minimal, wenn alle Punkte auf der Hauptdiagonalen liegen. Dann ist auch ein vollständiger Zusammenhang zwischen den Rängen gegeben.
Die Rangdifferenzen sind maximal, wenn alle Punkte auf der gepunkteten Diagonalen liegen. Dann ist auch ein vollständiger, umgekehrter Zusammenhang zwischen den Rängen gegeben.
Um die Rangdifferenzen zusammenzufassen, werden sie quadriert und über die Anzahl der Merkmalsträger aufsummiert.
Die empirisch ermittelte Summe der quadrierten Rangdifferenzen wird ins Verhältnis gesetzt zur maximal möglichen Quadratsumme, die bei einem vollständig negativem Zusammenhang realisiert wird. Aus diesem Verhältnis resultiert die Formel für den Rangkorrelationskoeffizienten rs *)
Rangkorrelationskoeffizient nach Spearman 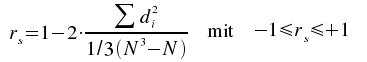
Ein alternativer, zum selben Ziel führender Weg, ist die Berechnung von rs als Korrelationskoeffizient nach Bravais-Pearson (vgl. Kap. XI-2) auf der Basis rangskalierter Variablen.
b) Der Wertebereich für den Rangkorrelationskoeffizienten
Wenn ein vollständig gleichgerichteter Zusammenhang gegeben ist, wird 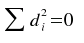 und rs = +1. und rs = +1.
Bei einem vollständig umgekehrten Zusammenhang wird 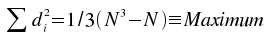 und rs = -1. und rs = -1.
Wird die Maximalsumme nur zur Hälfte erreicht, wird rs = 0.
2. Die Anwendung des Rangkorrelationskoeffizienten
Die Verwendung von rs ist an folgende strikte Voraussetzungen gebunden:
Die Daten liegen in Form von Rangreihen vor. Dem Zusammenhang liegt eine monotone Funktion zugrunde
Es liegen keine oder nur sehr wenige Ties vor.
*) Zur Ableitung vgl. Litz, Statistische Methoden, 3. Aufl., S 154.
|



