 |
Konzepte und Definitionen im Modul X-2 Konkordanzmaße für klassierte Daten
1. Das Konkordanzmodell bei Tabellendaten
In den bisher behandelten Beispielen war die Fallzahl N stets sehr klein, so dass mit Rohwerten gearbeitet werden konnte. Mit zunehmendem N wird es dann notwendig, diese Fälle durch Klassierung zusammen zu fassen und die Verteilung in die Form einer zweidimensionalen Häufigkeitstabelle zu bringen.
a) Die Ausgangstabelle
Tabelle 10-4: Einkommen und Mietausgaben
|
|
Einkommen von 0 bis unter 1200 EUR
|
Einkommen von 1200 bis unter 1800 EUR
|
Einkommen von 1800 bis unter 5000 DM
|
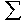
|
|
Miete von 0 bis unter 300 EUR
|
794
|
360
|
151
|
1305
|
|
Miete von 300 bis unter 500 EUR
|
646
|
701
|
524
|
1871
|
|
Miete von 500 EUR und mehr
|
103
|
287
|
441
|
831
|
|
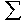
|
1543
|
1348
|
1116
|
4007
|
Aus dieser lassen sich konkordante und diskordante Paare analog zum bisherigen Vorgehen auszählen.
b) Die Ermittlung der konkordanten Paare
Die Konkordanten Paare sind dabei von Feld zu Feld zu berechnen.
Dabei geht man von den Fällen im linken oberen Tabellenfeld aus und bestimmt die zu diesen Fällen konkordanten Paare. Das sind diejenigen Paare, die sowohl über ein höheres Einkommen verfügen, wie höhere Mieten zahlen.
Diese sind im Schaubild 10-1 dargestellt. Als nächstes Feld ist das darunter liegend zu betrachten. Dafür ergeben sich die Paare aus dem Schaubild 10-2.
|
Schaubild 10-1: Konkordante Paare zum 1. Tabellenfeld
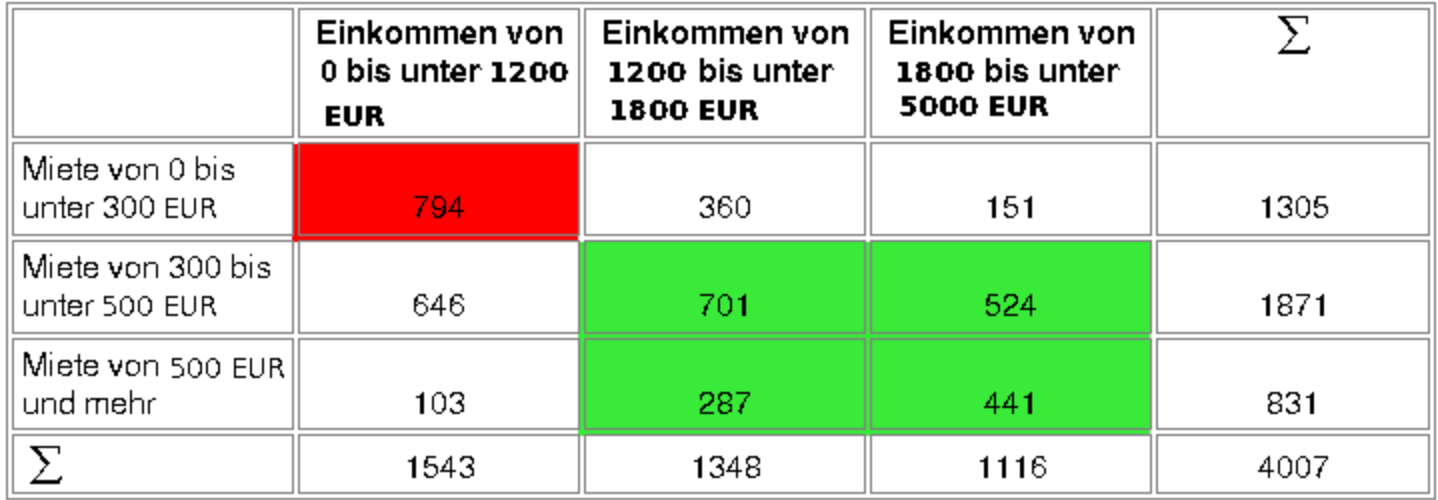
NK = 797(701 + 524 + 287 + 441) = 1.550 682. |
|
Schaubild 10-2: Konkordante Paare zum 2. Tabellenfeld
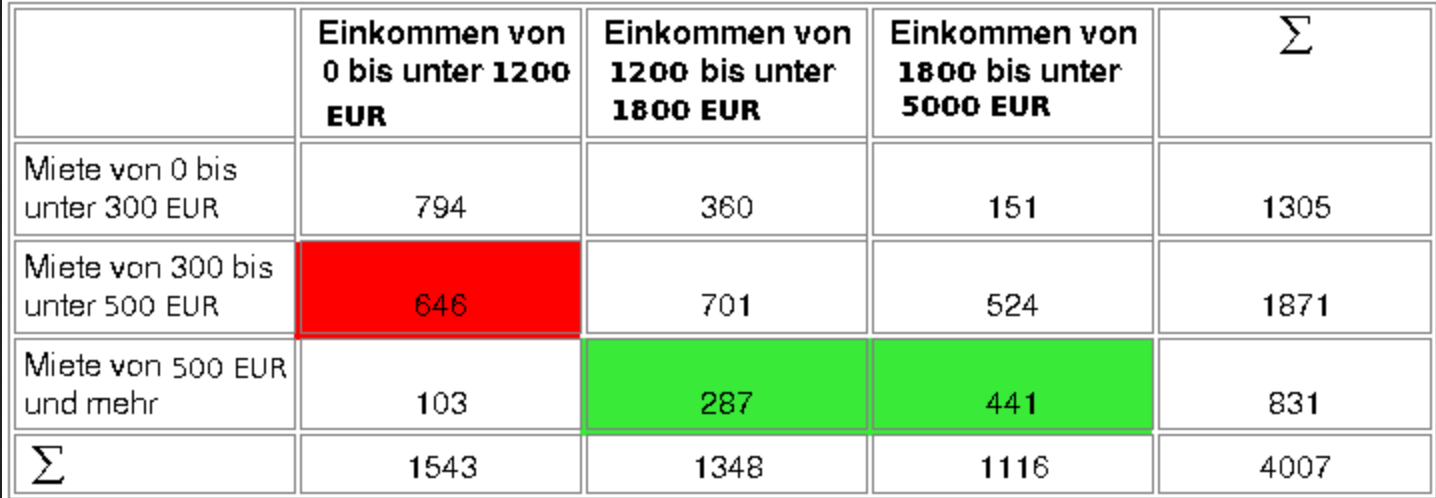
NK = 646(287 + 441) = 470 288.
|
Bei den nächsten Paaren ist vom obere Feld der zweiten Spalte auszugehen. Dafür ergeben sich die Paare im Schaubild 10-3. Schließlich bleiben noch die Paaren vom darunter liegenden Feld. Dafür ergeben sich die Paare im Schaubild 10-4.
|
Schaubild 10-3: Konkordante Paare zum 3. Tabellenfeld
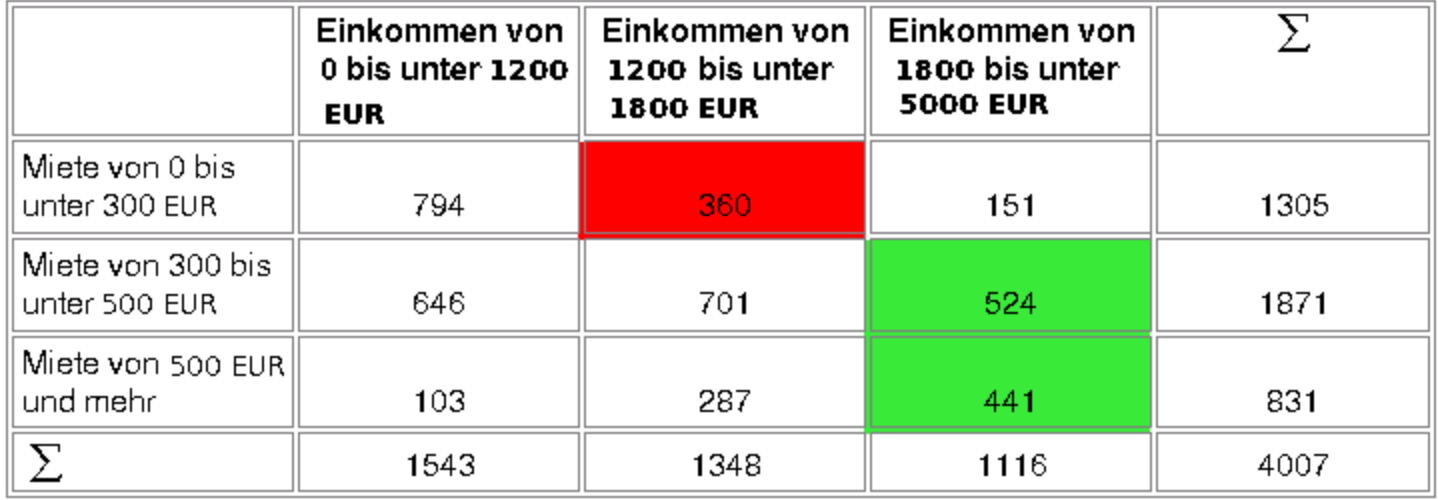
NK = 360(524 + 441) = 347 400.
|
|
Schaubild 10-4: Konkordante Paare zum 4. Tabellenfeld
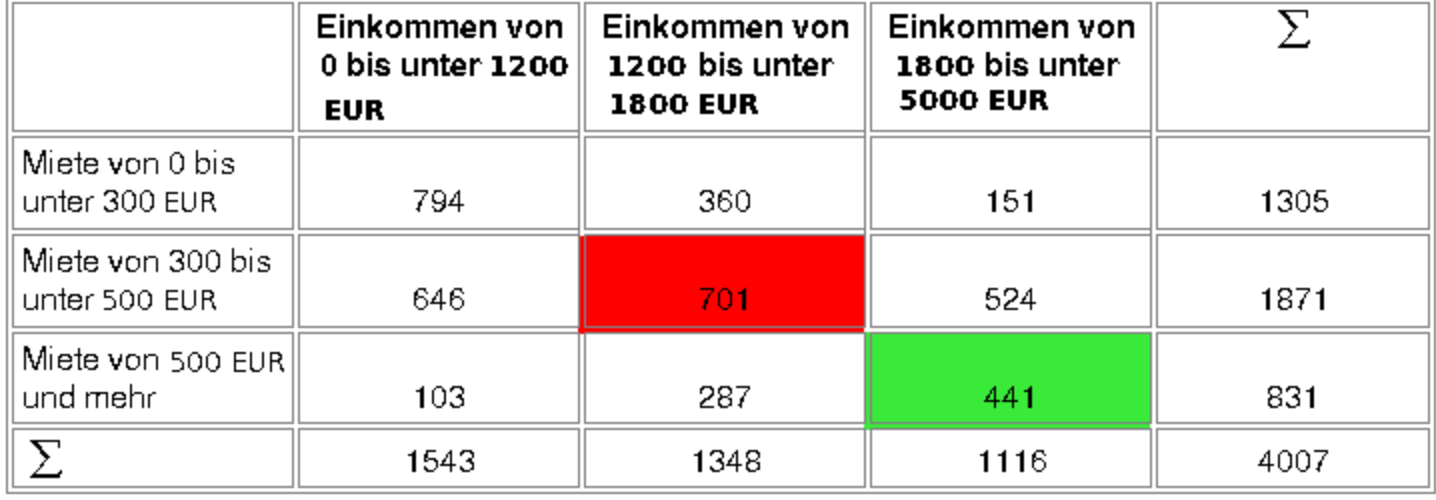
NK = 701 * 441 = 309 141.
|
Insgesamt erhalten wir NK = 2.677 511 konkordante Paare .
c) Die Ermittlung der diskordanten Paare
Analog zu den konkordanten Paaren werden auch die diskordanten Paare schrittweise ermittelt. Dabei ist umgekehrt vorzugehen und mit dem unteren Feld der ersten Spalte zu beginnen. Eine Abfolge der Schritte ist auf der nächsten Seite als Simulation abzurufen. Deshalb soll hier nur das Rechenergebnis präsentiert werden.
Danach ergibt sich die Anzahl der diskordanten Paare wie folgt:
Nd = 103(360 + 151 +701 + 524) + 646(360 + 151) + 287(151 + 524) + 701*151 = 808 490
d) Die Ermittlung der Ties
Durch die Klassierung entstehen allerdings gleiche ordinale Merkmalsausprägungen und man wird viele Fälle erhalten, die sich hinsichtlich einer oder beiden Variablen gleichen. Daraus resultiert ein sehr starker Anstieg der Ties.
So bilden z. B. alle fij Fälle eines Tabellenfeldes 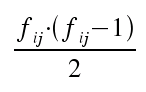 Ties in X und Y. Ties in X und Y.
Alle Fälle einer Tabellenzeile bilden Ties in Y und alle Fälle einer Tabellenspalte Ties in X. Eine Abfolge der Ermittlungsschritte ist auch auf der nächsten Seite als Simulation abzurufen.
Insgesamt ergibt sich eine Zahl von T = 4.540 020 Ties , die die Zahl der konkordanten und diskordanten Paare weit übertrifft.
e) Die Positionierung der Paare in der Tabelle
Die Position der konkordanten und der diskordanten Paare sowie der Ties in einer Tabelle finden sich in einer tabellarischen Darstellung im Materialanhang.
2. Das Konkordanzmaße bei unterschiedlicher Behandlung der Ties
a) Die Relevanz der Ties
Diese Ties sprechen nun auf den ersten Blick weder für noch gegen einen gerichteten Zusammenhang. Allerdings weicht nun die Summe aus konkordanten und diskordanten Paaren sehr stark von der Gesamtzahl der Paare ab. Für Kendall's τa hätte das zur Folge, dass das Maß nicht mehr im maximal möglichen Wertbereich ±1 liegt.
Die Konkordanzmaße für klassierte Daten unterscheiden sich deshalb vom einfachen Maß τa vor allem durch die explizite Berücksichtigung der Ties in unterschiedlichen Varianten. Diese sind in der folgenden Übersicht zusammengestellt.
b) Die Konkordanzmaße unter Berücksichtigung der Ties
Übersicht 10-1: Konkordanzmaße für Tabellendaten
|
Zusammenhangsmaß
|
Formel
|
Eigenschaften
|
|
Kendall's Tau
|
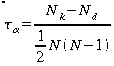
|
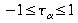 wenn
keine Ties vorkommen wenn
keine Ties vorkommen
|
|
|
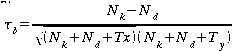
|
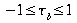 für
quadratische Tabellen für
quadratische Tabellen
|
|
|
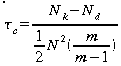
m=min(s,z)
|
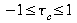 für
rechteckige Tabellen für
rechteckige Tabellen
|
|
Somer's d
|
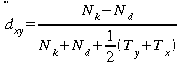
|
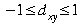
|
|
|
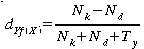
|
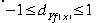
Annahme: Y ist eine Funktion von X
|
|
|
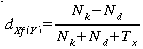
|
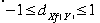
Annahme: X ist eine Funktion von Y
|
|
Goodman/Kruskal's gamma
|
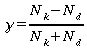
|
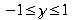
Keine Berücksichtigung von Ties
|
c) Die Einschätzung der verschiedenen Konkordanzmaße
Bei der Betrachtung dieser Maße ist zu beachten, dass beim Vorliegen vieler Ties das Maß τα i. A. einen Zusammenhang stark unterschätzt.
Eine Mittelung von Ties wie in τb oder dxy ist ebenfalls nur in Ausnahmefällen hilfreich, da Ties in X und Ties in Y nicht gleich zu behandeln sind.
Eine Möglichkeit das Problem zu umgehen, bietet Goodma/Kruskals γ, wo die Ties weder in Zählen noch im Nenner enthalten sind. Dies ist das Maß, dass bei gleicher Datenlage die höchsten Werte liefert.
Allerdings ist zu bedenken: Wenn Y eine Funktion von X ist:Y = f(X), dann wäre bei einer Veränderung von X eine Veränderung von Y zu erwarten und nicht dessen Konstanz. Deshalb sprechen Ties in Y eher gegen einen wie auch immer gerichteten Zusammenhang. Sie müssen dann auf jeden Fall im Nenner der Formel berücksichtigt werden.
Umgekehrtes gilt dann, wenn der Zusammenhang X = f(Y) zu vermuten ist.
Deshalb ist Somer's dY=f(X) bzw. Somer's dX=f(Y) bei dem jeweils unterstellten funktionalen Zusammenhang das geeignetste Maß aus dieser Übersicht.
c) Weitere Hinweise zu den Formeln
Ein Entscheidungsbaum zur Wahl der angemessenen Formel und weiter Erläuterungen zu den Formeln finden sich im Materialanhang.
|



