Beispiele und Aufgaben im Modul X-1 Konkordanzmaße bei Einzeldaten
1. Das Beispiel
a) Ein graphisches Auszählverfahren
Das im vorangegangenen Arbeitsschritt vorgestellte Auszählverfahren ist sehr kompliziert und fehlerträchtig, da leicht ein Paar übersehen
werden kann. Besser arbeitet man mit Hilfe des graphischen
Auszählverfahrens. Dazu werden die Ränge aller N Fälle
einfach in ein Koordinatensystem eingetragen. Welche Variable an X-
bzw. Y-Achse angetragen wird, ist dabei unerheblich!
Abbildung 10-1 Notenverteilung im ordinalen Koordinatensystem
|
Deutsch
|
5
|
|
|
|
|
*
|
|
|
4
|
|
|
*
|
|
|
|
|
3
|
*
|
|
|
|
|
|
|
2
|
|
|
|
*
|
|
|
|
1
|
|
*
|
|
|
|
|
|
|
1
|
2
|
3
|
4
|
5
|
|
Englisch
|
b) Eine Demonstration zum graphisches Auszählverfahren
Die konkordanten Paare erhält man wie folgt:
Man
beginnt bei dem rechten obersten Punkt - alle Punkte die links und
unterhalb dieses Punktes liegen sind konkordante Paare. Dann springt
man einen Punkt weiter nach links und wiederholt die Prozedur, bis
man links unten angekommen ist.
Zum Auszählen der diskordanten Paare wird analog
vorgegangen, nur dass jetzt alle links-oberhalb des
Referenzpunktes liegenden Fälle
gezählt werden.
Betrachten Sie das Auszählverfahren anhand dieser
Präsentationen:
 Auszählen
der konkordaten Paare im Koordinatensystem Auszählen
der konkordaten Paare im Koordinatensystem
 Auszählen
der diskordanten Paare im Koordinatensystem Auszählen
der diskordanten Paare im Koordinatensystem
In der Darstellung im Koordinatensystem
erscheinen Ties als nebeneinander bzw. übereinanderliegende
Punkte. Dies ist hier nicht der Fall.
c) Die Ergebnisse des graphischen Auszählverfahrens
Wir hatten durch den Paarvergleich NK = 7 konkordante und
ND = 3 diskordante Paare erhalten.
Auf dieser Grundlage kann nun Kendall's τa
berechnet werden.
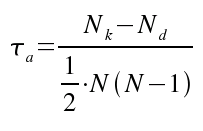
In unserem Beispiel erhalten wir:
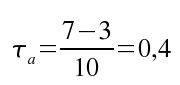
Dies ist ein Indiz für einen mittleren positiven Zusammenhang
zwischen den beiden Variablen.
2. Die Aufgabe
a) Die Aufgabenstellung
Um Verfahren zur Prüfung der Haltbarkeit von
Textilien so zu entwickeln, wurden an sieben
verschiedenen Textilien Trageversuche und verschiedene Scheuerversuche wie z.B. Biegescheuerung in Kett- und Schussrichtung durchgeführt.
Bei den Scheuerversuchen wurde die Anzahl der Scheuertouren bis zum
Bruch der Gewebe gezählt. Bei den Trageversuchen konnte man
lediglich eine Rangfolge in der Haltbarkeit der Textilien festlegen.
b) Die Ausgangstabelle
Tabelle 10-2: Haltbarkeitsversuche für Textilgewebe
|
Gewebeart
i
|
Rangzahl im Trageversuch
|
Scheuertouren bis zum Bruch der Gewebe
|
|
in Kettrichtung
|
in Schussrichtung
|
|
1
|
6
|
72
|
115
|
|
2
|
5
|
85
|
78
|
|
3
|
7
|
78
|
91
|
|
4
|
4
|
82
|
102
|
|
5
|
3
|
91
|
67
|
|
6
|
2
|
138
|
111
|
|
7
|
1
|
154
|
136
|
c) Die Vereinheitlichung der Skalierungen
Um zu prüfen, welcher
Kurzzeitversuch am besten geeignet ist, den Trageversuch zu ersetzen, müssen alle Variablen auf ein einheitliches (hier ein ordinale) Skalenniveau transformiert werden. Dabei sind die Ränge so zu vergeben, dass das Gewebe, das den meisten Scheuertouren standhält, "Rang 1" einnimmt und das mit der geringsten Anzahl von Scheuertouren "Rang 7".
Tabelle 10-3: Eingabe der Ränge der Scheuerversuche
d) Ergebniskontrolle
Berechnen Sie die Ergebnisse Ergebnisse für Nk, Nd und τα und geben Sie diese bitte auf zwei
Nachkommastellen gerundet ein.
Vergleich Trageversuch <-> Scheuerversuch in
Kettrichtung:
Ich habe folgende Ergebnisse für Nk, Nd
und
τα:
| 


