 |
Konzepte und Definitionen im Modul X-1 Konkordanzmaße bei Einzeldaten
1. Das Konkordanzmodell
a) Der Paarvergleich
Die Zusammenhangsmaße bei ordinalen Einzeldaten stützen sich, wie bereits ausgeführt, auf den Paarvergleich. Dazu werden die Merkmalsausprägungen zweier Merkmalsträger, etwa in einem schulischen Leistungsvergleich die Rangplätze zweier Schüler A und B in zwei Fächern miteinander verglichen.
Dieser Vergleich wird für alle möglichen Schülerpaare durchgeführt.
Mit dem Konkordanzmaß soll die Frage geklärt werden, ob ein Zusammenhang (eine Konkordanz) zwischen den Rangplätzen der Schüler etwa im Fach Englisch und ihren Rangplätzen im Fach Deutsch besteht und wie stark dieser Zusammenhang ist.
b) Konkordante und diskordante Paare
Konkordante Paare
Wird im Vergleich festgestellt, dass Schüler A sowohl in Englisch als auch in Deutsch besser ist als Schüler B, spricht dies für einen positiven Zusammenhang der beiden Variablen (also: je besser jemand in Englisch ist, desto besser ist er auch in Deutsch).
Man spricht dann von einem konkordanten (Schüler-)Paar. Das gleiche gilt für den Fall, dass Schüler A sowohl in Englisch als auch in Deutsch schlechter ist als Schüler B.
Diskordante Paare
Ist Schüler A jedoch in Englisch schlechter als Schüler B, dafür aber in Deutsch besser, würde dies für einen negativen Zusammenhang sprechen (also: Je besser jemand in Englisch ist, desto schlechter ist er in Deutsch).
Man spricht in diesem Fall von einem diskordanten Paar.
2. Die Konstruktion des Konkordanzmaßes
a) Die Differenz zwischen konkordanten und diskordanten Paaren
Die Logik der Konkordanzmaße liegt darin, die konkordanten gegen die diskordanten Paare zu verrechnen und die Differenz auf die Anzahl der möglichen Paare zu beziehen.
Dazu müssen alle Paarvergleiche durchgeführt werden und die Anzahl der konkordanten Paare (Nk) und der diskordanten Paare (Nd) ausgezählt werden.
Ist die Differenz also Nk - Nd positiv spricht man von einem positiven Zusammenhang, im umgekehrten Fall von einem negativen Zusammenhang.
b) Die Anzahl der Paare
Die Gesamtzahl der möglichen Paare { AB, AC,....YZ } lässt sich generell durch die Formel
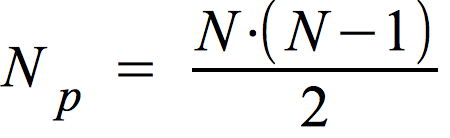
bestimmen.
c) Die Definition des Konkordanzmaßes Kendall's τa
Auf der Grundlage der Differenzen und der Gesamtzahl der Paare kann nun ein Maß für die Richtung und die Stärke des Zusammenhangsmaßes, das sog. Konkordanzmaß berechnet werden.
Das einfachste Konkordanzmaß, Kendall's τa ergibt sich wie folgt:
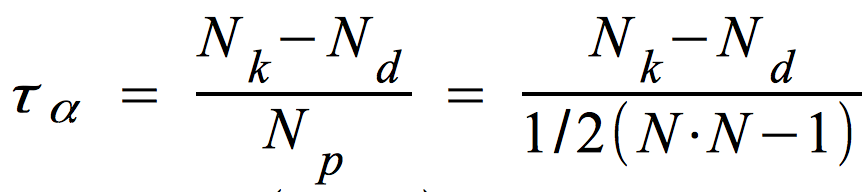 . .
d) Die Wertebereiche des Maßes Kendall's τa
Finden sich nur konkordante Paare (also Nk = Np), so nimmt τa den Wert + 1 an (max. positiver Zusammenhang).
Im umgekehrten Fall (Nd = Np) wird τa = - 1 (max. negativer Zusammenhang).
Treten gleich viele konkordante wie diskordante Paare auf, liegt kein statistischer Zusammenhang vor, dann wird τa gleich Null.
e) Die Ties
In einfachen Rangreihen sind meist nur konkordante und diskordante Paare zu finden. Bei klassierten Daten treten jedoch auch sog. Ties auf. Von Ties spricht man, wenn beim Paarvergleich zwei Fälle den gleichen Rang aufweisen. In einem solchen Falle wird das arithmetische Mittel der in Frage
kommenden Ränge zugewiesen. Lassen sich z.B. Rang 3 und 4 nicht
eindeutig vergeben, erhalten beide Fälle den Rang 3,5.
Dies kann entweder nur eine der beiden Variablen betreffen (Tie in X bzw. Tie in Y) oder auch beide Variablen (Tie in X und Y).
In diesen Fällen gilt:
Nk + Nd < Np
τa ist deshalb nur
geeignet, wenn keine Ties vorliegen. Es gilt dann (und nur dann):
-1 ≤ τa ≤ +1
Sollten bei einfachen Reihen doch Ties auftreten, muss auf alternative Maße ausgewichen werden. (Vgl. dazu die im Modul X-2, Übersicht 10-1 vorgestellten Varianten von τa).
3. Die Auszählung der Paare
Da die Auszählung, vor allem bei einer grösseren Anzahl von Fällen sehr aufwändig ist, soll sie an einer geringeren Fallzahl im Einzelnen demonstriert werden.
a) Die Ausgangstabelle
Angenommen, fünf Schüler erzielen folgende Noten in den
Fächern Deutsch und Englisch:
Tabelle 10-1 Schulleistungen in den Fächern Englisch und Deutsch
|
Schüler
|
A
|
B
|
C
|
D
|
E
|
|
Englisch
|
4
|
1
|
2
|
3
|
5
|
|
Deutsch
|
2
|
3
|
1
|
4
|
5
|
b) Die Simulation
In dieser Tabelle werden nun alle
Schüler paarweise miteinander verglichen:
Die folgende Präsentation
veranschaulicht das grundlegende Auszählverfahren:
Wenn Sie die Präsentation manuell steuern möchten,
klicken Sie bitte hier:

c) Das Ergebnis
|



