Konzepte und Definitionen im Modul V-1 Schiefe, Fechnersche Lageregel und Schiefemaße;
1. Das Konzept der Schiefe
Betrachten wir die graphische Darstellung der Wartezeiten in einer
Arztpraxis, wie sie im Histogramm in Kap. II erarbeitet wurde (vgl.
Abb. 5-1) so ist deutlich zu erkennen, dass die Verteilung nicht
symmetrisch ist, sondern nach links weniger steil, nach rechts
steiler abfällt.
Dieser Sachverhalt wird mit dem Begriff der
Linksschiefe bzw. der Rechtssteilheit beschrieben.
Abbildung 5-1: Verteilung der Wartezeiten in einer Arztpraxis
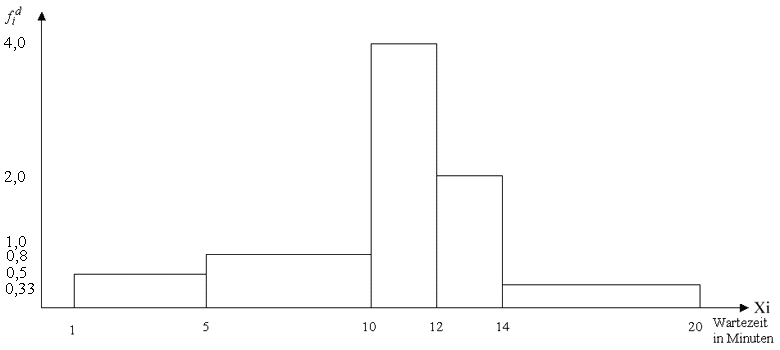
Wären die Häufigkeiten der Wartezeiten umgekehrt
verteilt, spräche man von Rechtschiefe und Linkssteilheit. Unter
diesem Aspekt der Schiefe sind drei Grundmodelle denkbar:
2. Die Grundmodelle der Schiefe
a) Die graphische Veranschaulichung
Abb. 5-2: Grundtypen der Schiefe:
|
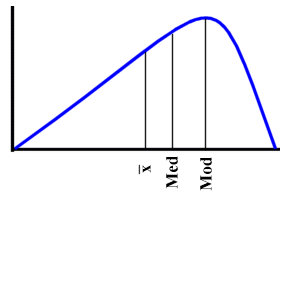
rechts-schief
(links-steil)
|
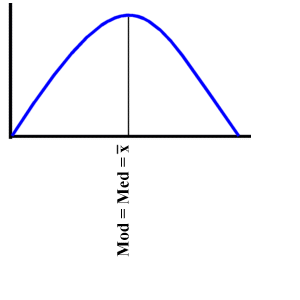
symmetrisch
|
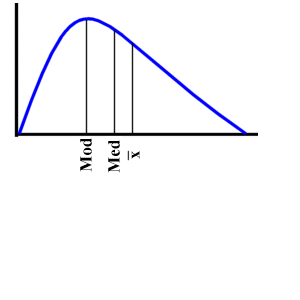
links-schief
(rechts-steil)
|
|
|
|
|
|
|
|
|
b) Die Reihenfolge der Mittelwerte
Aus der Graphik und den eingezeichneten Mittelwerten wird
erkennbar, dass die Reihenfolge der Mittelwerte mit diesem
Merkmals der Schiefe verknüpft ist:
|
rechts-schief
(links-steil)
|
symmetrisch
|
links-schief
(rechts-steil)
|
Dieser Sachverhalt lässt sich in der Fechnerschen
Lageregel verallgemeinern.
c) Die Fechnersche Lageregel
Die Fechnersche Lageregel ermöglicht die Beurteilung
einer Verteilung in Hinsicht auf die Schiefe, ohne dass eine
Grafik gezeichnet werden muss. Dazu werden
die Werte für Modus, Median und arithmetisches Mittel benötigt.
Aus ihnen lassen sich folgende Schlüsse ziehen:
|
Eine Verteilung ist ...
|
wenn ...
|
|
rechts-schief (links-steil)
|
Mod < Med <
|
|
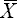
symmetrisch
|
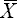
Med
Mod
|
|
links-schief (rechts-steil)
|
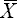< Med < Mod
|
d) Das Pearsonsche Schiefemaß
Ein quantitativer Ansatz, um die Schiefe zu beurteilen, ist das
Pearsonsche Schiefemaß (PSM).
Es wird nach der Formel:
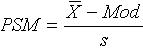
berechnet. Es gilt dabei:
Bei Symmetrie ist PSM=0, bei links-schiefen Verteilungen negativ
und bei rechts-schiefen positiv.
e) Das Schiefemaß v
Ein aufwändiger zu berechnendes Schiefemaß ist v:
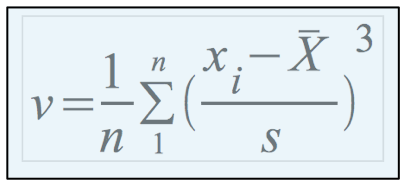
Für v gilt ebenfalls: Bei Symmetrie ist v=0, bei links-schiefen Verteilungen ist v negativ
und bei rechts-schiefen ist v positiv.
| 
