Wartezeit in Minuten
von... bis unter...
absolute Anzahl
fi
![]()
fi*mi
![]()
![]()
1-5
1
3
3
7,5
9
5-10
2
7,5
15
6
112,5
10-12
4
11
44
2
484
12-14
2
13
26
5
338
14-20
1
17
17
6,5
289
Summe:
10
-
105
27
1232,5
| Druckversion: | Nach dem Drucken: | und zurück zum Dokument |
Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken
| ViLeS 1 > IV Streuungsmaße > Rechnerische Streuungsmaße > Beispiele und Aufgaben |
Als Beispiel legen wir der Berechnung der Streuungsmaße die klassierte Tabelle der Wartezeiten in einer Arztpraxis zugrunde.
Für die Berechnung der mittleren quadratischer Abweichung und der Varianz benötigen wir weitere Spalten in unserer Arbeitstabelle.
Tab.4-3: Wartezeiten in einer Arztpraxis
|
Wartezeit in Minuten |
absolute Anzahl |
|
fi*mi |
|
|
|
1-5 |
1 |
3 |
3 |
7,5 |
9 |
|
5-10 |
2 |
7,5 |
15 |
6 |
112,5 |
|
10-12 |
4 |
11 |
44 |
2 |
484 |
|
12-14 |
2 |
13 |
26 |
5 |
338 |
|
14-20 |
1 |
17 |
17 |
6,5 |
289 |
|
Summe: |
10 |
- |
105 |
27 |
1232,5 |
Anmerkung:
![]() = 10,5 Minuten
= 10,5 Minuten
Für die mittlere absolute Abweichung erhalten wie aus der fünften Spalte dieser Tabelle :
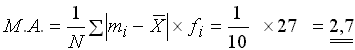
Für die Varianz ergibt sich aus der o.a. Tabelle (Spalte 6):
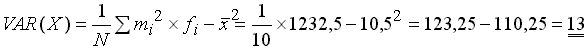
Für die Standardabweichung resultiert daraus:
![]()
und schließlich beträgt der Variationskoeffizient:
![]()
Zur mittleren absoluten Abweichung :
Empirisch am besten lässt sich die mittlere absolute Abweichung interpretieren. Im Durchschnitt warten danach die Patienten 2,7 Minuten weniger oder länger als 10,5 Minuten.
Zur Varianz und zur Standardabweichung:
Varianz und Standardabweichung basieren auf Durchschnitten von quadrierten Abweichungen. Das lässt sich so auch formulieren. Allerdings haben Quadrate von zeitlichen Differenzen keine reale Bedeutung. Die Relevanz dieser Streuungsmaße in der Statistik resultiert vor allem aus der induktiven Statistik (vgl. dazu ViLeS 2, Kap. II-2). Wenn die Wartezeiten normalverteilt wären, würden im Bereich ± s um das arithmetische Mittel etwa 66% der Beobachtungen liegen.
Auch der Variationskoeffizient unterliegt der obigen Einschränkung. Allerdings erlaubt er den Vergleich von Streuungen unterschiedlicher Verteilungen. So gibt der berechnete Wert von 0,34 einen Hinweis darauf, ob die Streuung der Wartezeiten, relativ gesehen, größer oder kleiner ist, als etwa die der Urlaubsausgaben der nachfolgenden Rechenaufgabe.
Als Beispiel legen wir der Berechnung der Streuungsmaße die klassierte Tabelle der Wartezeiten in einer Arztpraxis zugrunde.
|
|
Berechnen Sie für die nachfolgende Tabelle der studentischen Urlaubsausgaben:
Runden Sie Ihre Ergebnisse auf 4 Nachkommastellen! |
Tab. 4-4: Urlaubsausgaben von Studierenden
|
Nr. |
von ... EUR |
bis unter ... EUR |
Anzahl |
Klassenmitte |
|
|
|
1 |
0 |
250 |
17 |
125 |
2125 |
265.625 |
|
2 |
250 |
450 |
14 |
350 |
4900 |
1.715.000 |
|
3 |
450 |
550 |
9 |
500 |
4500 |
2.250.000 |
|
4 |
550 |
650 |
15 |
600 |
9000 |
5.400.000 |
|
5 |
650 |
750 |
13 |
700 |
9100 |
6.370.000 |
|
6 |
750 |
850 |
9 |
800 |
7200 |
5.760.000 |
|
7 |
850 |
1150 |
14 |
1000 |
14.000 |
14.000.000 |
|
8 |
1150 |
2150 |
5 |
1650 |
8250 |
13.612.500 |
|
9 |
2150 |
3350 |
4 |
2750 |
11.000 |
30.250.000 |
|
Summe: |
100 |
|
70.075 |
79.623.125 |
||
Eingaben zur mittleren absoluten Abweichung M.A.:
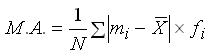 =
=
Vergleichen und interpretieren Sie die Ergebnisse!
Ist die relative Streuung der Urlaubsausgaben größer oder kleiner als die der Wartezeiten?
letzte Änderung am 28.2.2020 um 7:49 Uhr.
Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles1/kapitel04_Streuungsma~~sze/modul02_Rechnerische~~lStreuungsma~~sze/ebene02_Beispiele~~lund~~lAufgaben/04__02__02__0
1.php3