Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken

1. Vorbemerkung

Die rechnerischen Streuungsmaße basieren auf den Distanzen der einzelnen Beobachtungen (bei klassierten Daten: der Klassenmitten) vom arithmetischen Mittel. Diese Abstände und somit die darauf basierenden rechnerischen Mittelwerte sind nur für metrische Daten empirisch sinnvoll.

2. Die mittlere absolute Abweichung (M.A.)

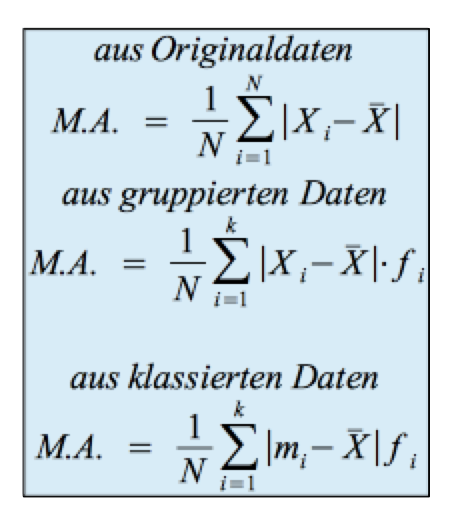
Bei der mittleren absoluten Abweichung (M.A.) gehen die positiven und negativen Abweichungen der Beobachtungen bzw. der Klassenmittelwerte m_i vom arithmetischen Mittel als absolute Werte in die Berechnung ein. Diese werden danach gemittelt.
Die Formel für die M.A. lautet:

2. Die Varianz (VAR)

Bei der Varianz (VAR) werden die Abstände zwischen den Beobachtungen bzw. Klassenmitten m_i und dem arithm. Mittel quadriert und gemittelt. Deshalb wird die Varianz auch als mittlere quadratische Abweichung bezeichnet.
Die Rechenformel ergibt sich durch Umformung der Ausgangsgleichung.

3. Die Standardabweichung

Die Standardabweichung s errechnet sich als Wurzel der Varianz:

4. Der Variationskoeffizient

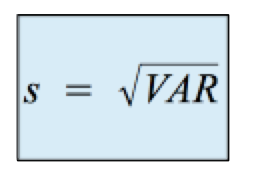
Der Variationskoeffizient (V) macht eine Aussage über die relative Streuung von Werten. Ihn nutzt man, wenn die Streuungen mehrerer Studien, die sich z.B. in zeitlicher oder regionaler Hinsicht unterscheiden, miteinander verglichen werden sollen. Er ist definiert als Verhältnis der Standardabweichung zum arithmetischen Mittel:

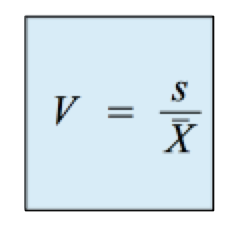
Multipliziert man den Variationskoeffizient mit 100, drückt er die relative Streuung in Prozent aus.

letzte Änderung am 28.2.2020 um 7:49 Uhr.

Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles1/kapitel04_Streuungsma~~sze/modul02_Rechnerische~~lStreuungsma~~sze/ebene01_Konzepte~~lund~~lDefinitionen/04__02__01
__01.php3