 |
Graphische Darstellung von Box-Plots im Modul IV-1 Lagetypische Streuungsmaße
1. Konzept und Konstruktion
a) Das Konzept der Box-Plots
Quartile und Quartilsabstände lassen sich in Form sog. Box-Plots (Box and Whiskers-Plots) auch graphisch darstellen. Diese Plots veranschaulichen die Lage einer Verteilungen durch den Median und die Streuung durch die Quartile und den Quartilsabstand.
Box-Plots sind vor allem für den Vergleich mehrerer Verteilungen gut geeignet.
Dazu werden im Koordinatensystem auf der Y-Achse die Merkmalsvariable Xi und auf der X-Achse die Unterscheidungsvariable (Kategorien-Variable) eingetragen. So können die Unterschiede der Verteilungen auf einen Blick verdeutlicht werden (vgl. Abb. 4-6).
Darüber hinaus lassen sich für die Verteilungen eventuelle Ausreißer und Extremwerte identifizieren und u.U. auf Datenfehler überprüfen.
b) Die Konstruktion des Box-Plot
Lage und Streuung der Merkmalsvariablen werden in Form eines vertikalen Rechteckes (der Box) visualisiert, deren untere Grenze dem 1. Quartil und deren obere Grenze dem 3. Quartil entspricht. Die Höhe der Box drückt also den Quartilsabstand (QA) aus.
Gleichzeitig wird in der Box durch den Median (2. Quartil) das Zentrum der Verteilung gekennzeichnet (vgl. Abb. 4-5).
Die von der Box ausgehenden Linien (Whiskers) und die begrenzenden Linien (Fences) markieren den kleinsten bzw. größten Wert innerhalb eines Bereichs von ± 1,5 QA unter bzw. über den Quartilen.
Werte außerhalb der Fences werden im Bereich ± 1,5 QA als Ausreißer (°), außerhalb dieses Bereichs als Extremwerte (*) nachgewiesen. Zur Datenkontrolle kann für diese Werte die Fallnummer ausgewiesen werden.
Der Abstand zwischen der untersten und der obersten Markierung entspricht der Spannweite.
Abb. 4-5: Die Konstruktion des Boxplot

2. Beispiel
a) Die Ausgangsdaten
Als Beispiel soll auf unsere Daten der Urlaubsausgaben zurückgegriffen werden, die dazu nach einer weiteren Variablen (Geschlecht: 46 w, 54 m) aufgesplittet werden. Die Daten entstammen einer getrennten Berechnung der Quartile mit Q1(w) = 210 EUR, Q1(m) = 545 EUR, Q3(w) = 600 EUR und Q3(m) = 903,75 EUR.
b) Die Box-Plots
Abb. 4-6: Boxplot Urlaubsausgaben nach Geschlecht
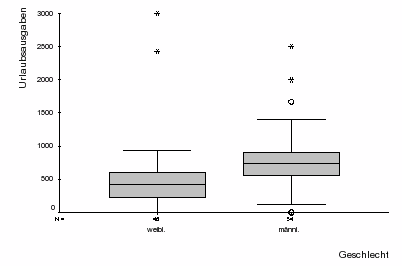
c) Die Interpretation der Plots
Man sieht in Abb. 4-6, dass die nach Geschlecht unterschiedenen Verteilungen der Urlaubsausgaben für die 46 weiblichen Studierenden einen niedrigeren Median (= 425 EUR gegenüber 736 EUR für die 54 männlichen), aber einen geringfügig größeren Quartilsabstand (390 EUR gegenüber 359 EUR) aufweisen.
Ausserdem werden alle Ausgaben von mehr als 1500 EUR als Ausreißer oder als Extremwerte gekennzeichnet.
3. Aufgaben
Nach der Präsentation der SPSS-Verfahren zur Berechnung der Streuungsmaße und zur Erzeugung von Box-Plots im nachfolgenden Modul IV-3 "Eigene Analysen und Interpretationen" können Sie die Verteilungen der Variablen "Partizipationsprofil" und "Partizipationspotential" für die einzelnen Kategorien der Variablen "Status" über Boxplots veranschaulichen und darüber Erkenntnisse gewinnen, ob und wie der betriebliche Status die Entscheidungsstrukturen bestimmt.
|



