| Druckversion: | | Nach dem Drucken: | | und zurück zum Dokument |
Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken
Die Behandlung von Ausreißern im Modul III-4 Mittelwerte in der Praxis
1. Die Ausgangsproblematik
Ausreißer sind Werte, die am Rand einer
Verteilung liegen und einen mehr oder weniger großen Abstand zu
den Werten im Zentrum aufweisen. Diese Ausreißer haben Einfluss;
auf die optisch Erscheinung der Verteilung, aber auch auf Mittelwerte, genauer gesagt auf das arithmetische Mittel - denn
Modus und Median sind unempfindlich gegen Ausreißer - und auch auf die noch zu behandelnden Maßzahlen der Streuung.
Um die
Problematik aufzuzeigen, bedienen wir uns nochmals der
Urlaubsausgaben der Oldenburger Studenten. Deren Verteilung
sieht im Original wie folgt aus :
Abb. 3-10: Verteilung der Urlaubsausgaben
von Studierenden
Abbildung 2-8: Histogramm der fiktiven Urlaubs-Ausgaben
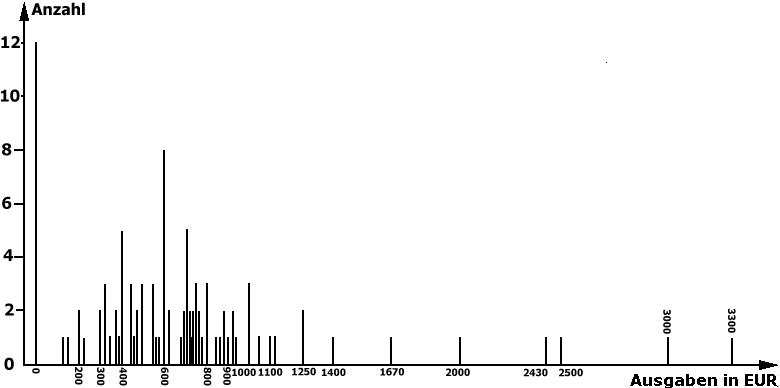
Zu ihrer genauen Definition bezieht man sich auf den Abstand der Merkmalswerte der zentralen 50% der Fälle (vgl. dazu das Kapitel "Streuungsmaße" und dort das Konzept des Quartilsabstandes in Verbindung mit seine graphischen Darstellung im "Box-Plot").
Weichen Beobachtungen um mehr als das 1,5 fache von diesen Merkmalswerten ab, spricht man von Ausreißern. Bei einer Abweichung um mehr als dem 3-fachen werden die Beobachtungen als Extremwerte bezeichnet.
2. Der Umgang mit Ausreißern und Extremwerten
Vorab ist für diese Fälle zu prüfen, ob es sich dabei um fehlerhafte bzw. unplausible Werte handelt. Ist dies eindeutig festzustellen, sollten diese Werte als "missing values" deklariert werden.
a) Untypische Fälle am unteren Rand der Verteilung
Entfernt man nun die Studierenden, die vermutlich nicht im Urlaub waren, d.h. die
Gruppe "0 EUR", so ergeben sich folgende Mittelwerte:
|
Anzahl der Fälle
|
88,00
|
|
arithmetisches Mittel
|
769,00
|
|
Modus
|
600,00
|
|
Median
|
685,00
|
|
Spannweite
|
3180,00
|
Durch die Elimination steigt der Median von 600 auf 685 EUR und das arithmetische Mittel von 675,97 auf
769 EUR.
b) Untypische Fälle am oberen Rand der Verteilung
Eliminiert man aus dieser Grafik zusätzlich alle Personen mit einem Einkommen über 1400 EUR, ergibt
sich folgendes Bild:
Abb. 3-11: korrigierte Urlaubsausgaben
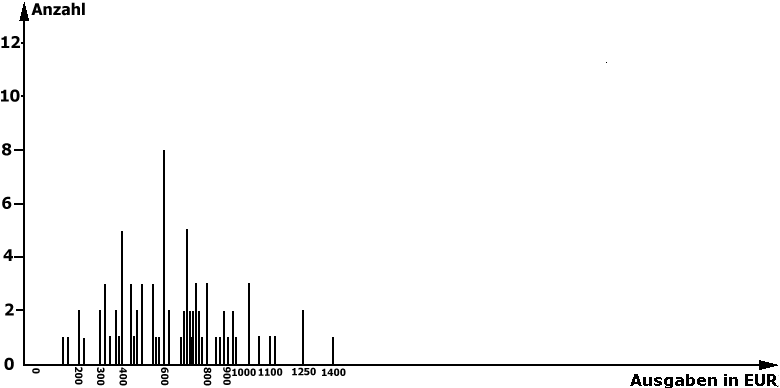
Das Resultat zeigt sich selbstverständlich
nicht nur in der Grafik, die eine deutlich symmetrische Gestalt annimmt, sondern hat auch direkte Auswirkungen auf
die Maßzahlen:
|
Anzahl der Fälle
|
82,00
|
|
arithmetisches Mittel
|
642,01
|
|
Modus
|
600,00
|
|
Median
|
600,00
|
|
Spannweite
|
1280,00
|
Es zeigt sich, dass sowohl das arith. Mittel
wie auch der Median sich verändern. Am deutlichsten verändert
sich durch die Eliminierung der Ausreißer das arith. Mittel. Der Median nimmt wieder seinen ursprünglichen Wert an. Ob und
wie weit sich der Median verändert, hängt davon ab, wie
dicht die Werte im Zentrum beieinander liegen. Der Modus bleibt
konstant bei 600 EUR, da sich der häufigste Werte nicht verändert
hat.
c) Die Bereinigung der Daten um Ausreißer
Eine Bereinigung der Daten um Ausreißer ist in der
empirischen Analyse ein kritisches Unterfangen, da damit eventuellen
Manipulationen Tür und Tor geöffnet wird. Eine Zulässigkeit
hängt davon ab, ob sie die Kernaussage der Verteilung verfälscht
oder präzisiert. Im Falle der Studierenden kann man bei Urlaubsausgaben von mehreren Tausend Euro berechtigte Zweifel haben,
ob die betreffenden Personen nicht eher als Vollzeiterwerbstätige mit entsprechendem Urlaubsverhalten
denn als reguläre Studierende aufzufassen sind.
Andererseits ist es auch möglich, dass die Betreffenden für diesen Urlaub angesparte oder sonstwie erhaltene Mittel eingestzt haben.
In der explorativen Datenanalyse und in den
statistischen Analyseprogrammen wurden in den vergangenen Jahren das
sog. gestutzte arithmetische Mittel eingeführt, das in der Regel die
unter und oberen 5 % der Fälle ausschließt.
letzte Änderung am 28.2.2020 um 7:49 Uhr.
Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles1/kapitel03_Mittelwerte/modul04_Mittelwerte~~lin~~lder~~lPraxis/ebene02_Aussage~~lder~~lMittelwerte/03__04__02__01.ph
p3

