 |
Aussage und Auswahl der Mittelwerte im Modul III-4 Mittelwerte in der Praxis
1. Die Aussagen statistischer Mittelwerte
a) Die Charakterisierung des Zentrums einer Verteilung
In der empirischen Datenanalyse reicht es bei weitem nicht aus, die statistischen Maßzahlen zu berechnen und deren Werte zu benennen. Unabdingbarer Teil der Analyse ist die Interpretation der Ergebnisse, d.h. die Angabe dessen, was diese Zahlenwerte über die Realität aussagen.
Alle in diesem Kapitel behandelten Maßzahlen sind Mittelwerte, also Modelle, die das Zentrum einer Häufigkeits-Verteilung beschreiben. Ihre Aussagen
beziehen sich entsprechend ihrer jeweiligen Modelllogik u.U. auf verschiedene
Aspekte der Realität - etwa wie ein Stadtzentrum als geographisches (geographischer Mittelpunkt), verkehrstechnisches (Hauptbahnhof), ökonomisches (Einkaufzentrum), soziales (Marktplatz) oder politisches Zentrum (Rathaus) verstanden werden kann.
Insofern gibt es - ausser bei einer fehlerhaften Ermittlung - keine richtigen bzw. falschen Mittelwerte, sondern nur im Sinne der Untersuchung adäquate und inadäquate Mittelwerte.
b) Das Beispiel der Wartezeiten
Um die Aussagen der einzelnen Mittelwerte zu
vergleichen, sind hier die Beträge der Mittelwerte der Wartezeiten aus unserem
Beispiel aufgeführt und auf einander bezogen:
|
arithmetisches Mittel:
|
|
10,5 Min.
|
|
Median:
|
|
11,0 Min.
|
|
Modus:
|
|
11,2 Min
|
Zum
arithmetischen Mittel: Im rechnerischen Durchschnitt warten die
Patienten 10,5 Minuten. Diese Zeit würde sich ergeben, wenn alle
Personen gleich lang warten müssten.
Zum
Modus: Am häufigsten wurde eine Wartezeit zwischen 10 und 12
Minuten genannt. Eine genauere Abschätzung für die Spitze der Wartezeiten innerhalb dieser Klasse ergab 11,2 Min. Dies bedeutet, dass
die größte Teilgruppe der Patienten länger wartet als
sie es bei einer Gleichverteilung der Wartezeit müsste.
Zum Median: Die Aussage des
Medians ist: 50% der der Wartezeiten lagen unter 11 Minuten,
50% über 11 Minuten.
Liegen Modus, Median und
arithmetisches Mittel, wie im Beispiel, dicht beieinander, so
unterscheiden sich die quantitativen Aussagen nicht sehr. Der Grund
für das niedrigere arithmetische Mittel sind einige recht
geringe Wartezeiten (hier impliziert in den größeren
Klassenbreiten der beiden Eingangsklassen), welche den Durchschnitt
nach unten ziehen. Oft führen allerdings recht große Werte
in den Beobachtungen dazu, dass das arithmetische Mittel über
den lagetypischen Mittelwerten liegt. Wir werden auf diesen Problem
bei der Behandlung von Ausreißern zurückkommen.
c) Das Beispiel der Urlaubsausgaben
Zu diesem Beispiel wollen wir nicht nur die Ergebnisse der einzelnen Mittelwert-Typen
vergleichen, sondern auch noch die Berechnungen aus gruppierten und aus klassierten Darten einander gegenüberstellen:
Tabelle 3-11: Mittelwerte der Urlaubsausgaben
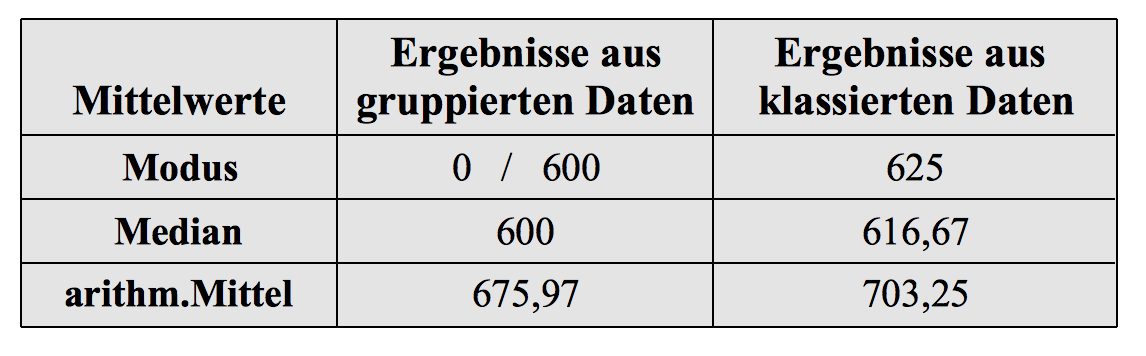
Beim Vergleich der verschiedenen Typen und Ausgangsdaten ist folgendes bemerkenswert:
Alle Mittelwerte liegen im Bereich von etwa 600 - 700 EUR.
Dabei errechnen sich die exakten Ergebnisse immer aus den nicht-klassierten Daten. Der aus der Klassierung resultierende Informationsverlust weist den darüber berechneten Ergebnissen den Status von annähernden Werten zu.
Im konkreten Beispiel fallen die Werte aus den nicht-klassierten Daten für alle drei Typen etwas kleiner aus als die Werte aus den klassierten Daten. Dies liegt daran, dass die Beobachtungen innerhalb der Klassen nicht gleichmäßig verteilt sind, sondern eher in der oberen Hälfte liegen.
Bezüglich der modalen Werte kann natürlich der häufigste Wert "0" nicht als Mittelwert genommen werden. Der zweithäufigste Wert "600" stimmt mit dem exakten Median überein.
Das arithmetische Mittel weicht in beiden Fällen stark von den modalen und medianen Ergebnissen ab. Dies liegt an der größeren Anzahl von sehr hohen Urlaubsausgaben von über 1500 EUR. Wie mit diesen Ausreissern zu verfahren ist, wird im nächsten Arbeitsschritt eingehender diskutiert.
Als Fazit ist deshalb festzuhalten, dass alle drei Mittelwerte zur Charakterisierung der Verteilung wichtige Informationen liefern, dass aber der Median und auch der Modus am ehesten für einen typischen Urlaub stehen.
2. Die Auswahl der statistischen Mittelwerte
a) Die Vollständigkeit der Auswahl
Ziel einer empirischen Analyse ist die vollständige Ausschöpfung der Informationen, die in einem Datensatz vorliegen. Aus diesem Grund ist es meist sinnvoll, soweit
es vom Skalenniveau her zulässig ist, möglichst alle
Mittelwerte zur Charakterisierung einer Häufigkeitsverteilung
einzusetzen und ihr Verhältnis zu diskutieren.
Aus dem
Vergleich der Mittelwerte kommt noch ein zusätzlicher Aspekt ins Blickfeld:
der der Reihenfolge der verschiedenen Mittelwerte und damit der der Symmetrie bzw. der der Schiefe einer Verteilung. Darauf wird in Kap. 5
zurückgekommen.
b) Die Problematik einer selektiven Auswahl
Wenn schon nur ein
Mittelwert ausgewählt wird, dann nicht nach dem Kriterium, dass
der genehmste Mittelwert der richtige ist. Etwa der Art: Soll die
Aussage sein, dass der Mittelwert eher gering ist, bedient man
sich des arithmetischen Mittels ("Die Wartezeit beträgt im
Schnitt nur 10,5 Min."), im anderen Fall ("Die meisten
Befragten warten 11,2 Min.") des Modus.
Auch am Beispiel der Urlaubsausgaben, in dem eine beträchtliche
Anzahl hoher Merkmalswerte zu beobachten ist - also eine schiefe
Verteilung vorliegt -, ist es notwendig alle Mittelwerte
heranzuziehen und ihre Aussagen als empirische
Charakteristik der Verteilung zu nutzen.
Zu dieser Problematik ein Auszug und eine Karikatur aus Krämer,
W.; So lügt man mit Statistik; 8. Auflage; Campus Verlag; FFM:
1998; Seite 65-66:
|
"Wenn also der Präsident der
Bundesärztekammer vom mittleren Einkommen der deutschen
Ärzte spricht, meint der in der Regel nicht das
arithmetische Mittel, sondern den Median. Wann immer im Deutschen
Ärzteblatt von Geld die Rede ist, erinnert man sich
gerne daran, dass es außer dem arithmetischen Mittel
auch noch andere Mittelwerte gibt.
Auf der anderen Seite rufen
Kritiker, die meinen, deutsche Ärzte verdienen viel zu viel,
gern das arithmetische Mittel in den Zeugenstand; dieses ist viel
größer als der von den Ärzten selbst bevorzugte
Median. Ein niedergelassener Laborarzt etwa verdient nach Abzug
der Praxiskosten, wenn man das arithmetische Mittel nimmt,
durchschnittlich 700000 Mark im Jahr, beim Median dagegen 200000
DM weniger [...]."
|
Plastisch wird das Argument durch ein weiteres Zitat aus Krämer, W. ("So lügt man mit Statistik", ebenda)
|

|
|
"Sollen wir das arithmetische Mittel als
durchschnittliche Körpergröße nehmen und den
Gegner erschrecken, oder wollen wir ihn einlullen und nehmen den
Median?"
|
|
Krämer, W.; So lügt man
mit Statistik; 8. Auflage; Campus Verlag; FFM: 1998; Seite 65
|
|



