Wartezeit in Minuten
von... bis unter...
fi
Klassenbreite![]()
![]()
1-5
1
4
1
5-10
2
5
3
10-12
4
2
7
12-14
2
2
9
14-20
1
6
10
Summe:
10
-
-
| Druckversion: | Nach dem Drucken: | und zurück zum Dokument |
Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken
| ViLeS 1 > III Maße der zentralen Tendenz (Mittelwerte) > III 2 Der Median > Beispiele und Aufgaben zur graphischen Ermittlung |
Im Rechenbeispiel bezogen wir uns
auf die Tabelle 2-14 der absoluten und kumulierten Wartezeiten in einer Arztpraxis aus dem Kap.II-3.
Tabelle 3-7: absolute und kumulierte Wartezeiten in
Minuten
|
Wartezeit in Minuten |
fi |
Klassenbreite |
|
|
1-5 |
1 |
4 |
1 |
|
5-10 |
2 |
5 |
3 |
|
10-12 |
4 |
2 |
7 |
|
12-14 |
2 |
2 |
9 |
|
14-20 |
1 |
6 |
10 |
|
Summe: |
10 |
- |
- |
Die graphische Bestimmung des Median erfolgt mit Hilfe des Summenpolygons, welches bereits in Kap. II besprochen und gezeichnet wurde.
Dieses ergibt sich wie folgt aus den obigen Daten:
Abbildung 3-7: Summenpolygon der Wartezeiten
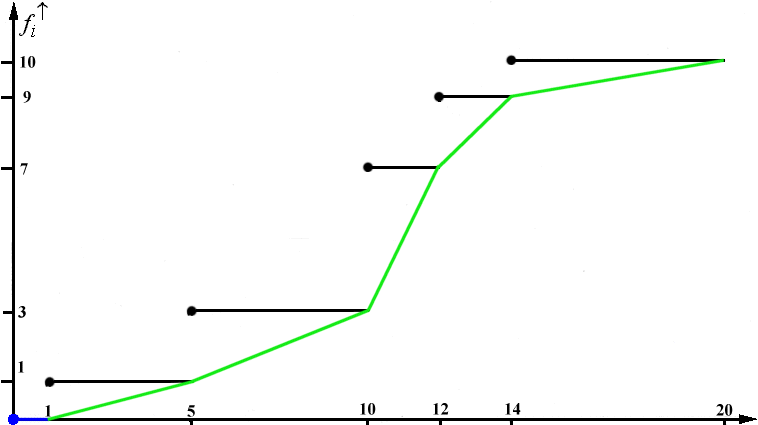
Zunächst wird auf der Y-Achse der "N / 2"-Wert gesucht, der hier 5 ist. Von dort aus zieht man eine waagerechte Linie, bis diese das Summenpolygon trifft. Der Median ist der Wert auf der X-Achse, an dem das Lot auf den Schnittpunkt die Achse trifft.
Abb. 3-6: Graphische Ermittlung des Medians
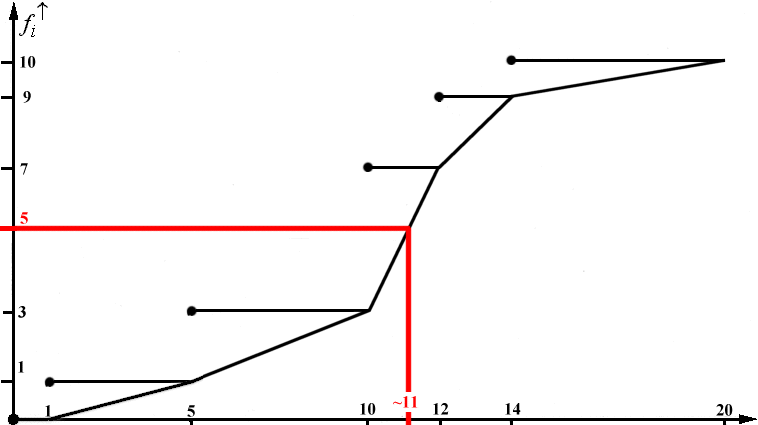
Wie beim Modus liefert der rechnerische Median exaktere Werte, da
bei Zeichnungen immer Ungenauigkeiten vorhanden sind.
Anmerkung: Die Formel für
den feinberechneten Median im Abschnitt III-1 (1) ergibt sich aus einem Strahlensatz, der
sich zur obigen Graphik für die Klasse 10 - bis unter 12 formulieren lässt (zum
Einzelnen vgl. Litz, 2003, S. 18 ff.).
|
|
Bestimmen Sie graphisch den Median für das Summenpolygon der Urlaubsausgaben von Studierenden. Dieses wurde zu den Daten der Tab. 3-6 bereits in einer Aufgabe im Modul II-3 von Ihnen gezeichnet. |
Tabelle 3-8: Urlaubsausgaben von Studierenden
|
Nr. |
von ... EUR |
bis unter ... EUR |
Anzahl |
Klassenmitte |
abkum. Hf. |
kum. Hf. |
|
1 |
0 |
250 |
17 |
125 |
83 |
17 |
|
2 |
250 |
450 |
14 |
350 |
69 |
31 |
|
3 |
450 |
550 |
9 |
500 |
60 |
40 |
|
4 |
550 |
650 |
15 |
600 |
45 |
55 |
|
5 |
650 |
750 |
13 |
700 |
32 |
68 |
|
6 |
750 |
850 |
9 |
800 |
23 |
77 |
|
7 |
850 |
1150 |
14 |
1000 |
9 |
91 |
|
8 |
1150 |
2150 |
5 |
1650 |
4 |
96 |
|
9 |
2150 |
3350 |
4 |
2750 |
0 |
100 |
|
Summe: |
100 |
|
||||
Mit dem integrierten Programm Häufigkeitstabellen
zur Analyse klassierter Daten können Sie durch Eingabe der klassierten Tabelle den Median per Programm graphisch ermitteln und Ihr manuell erzeugtes Ergebnis auf Korrektheit überprüfen.
letzte Änderung am 28.2.2020 um 7:49 Uhr.
Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles1/kapitel03_Mittelwerte/modul02_Der~~lMedian/ebene03_Beispiele~~lund~~lAufgaben~~lzur~~lgraphischen~~lErmittlung/03__
02__03__01.php3