Wartezeit in Minuten
von... bis unter...
fi
Klassenbreite![]()
![]()
1-5
1
4
1
5-10
2
5
3
10-12
4
2
7
12-14
2
2
9
14-20
1
6
10
Summe:
10
-
-
| Druckversion: | Nach dem Drucken: | und zurück zum Dokument |
Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken
| ViLeS 1 > III Maße der zentralen Tendenz (Mittelwerte) > III-2 Der Median > Beispiele und Aufgaben zur rechnerischen Ermittlung |
Im Beispiel beziehen wir uns wieder
auf die Tabelle der absoluten und kumulierten Wartezeiten in einer Arztpraxis aus dem Kap.II-3.
Tabelle 3-5: absolute und kumulierte Wartezeiten in
Minuten
|
Wartezeit in Minuten |
fi |
Klassenbreite |
|
|
1-5 |
1 |
4 |
1 |
|
5-10 |
2 |
5 |
3 |
|
10-12 |
4 |
2 |
7 |
|
12-14 |
2 |
2 |
9 |
|
14-20 |
1 |
6 |
10 |
|
Summe: |
10 |
- |
- |
Unter Beachtung der einzelnen Ausdrücke in der Formel:
|
|
Klassenunterrand der medianen Klasse |
|
|
Klassenbreite der medianen Klasse |
|
|
Summe der Häufigkeiten unterhalb der medianen Klasse |
|
|
Häufigkeit in der medianen Klasse |
ergibt sich der Median wie nachstehend:
Dabei ist die mediane Klasse die markierte, dritte Klasse, da erst dort der von N/2=5 erreicht bzw. hier: überschritten wird.
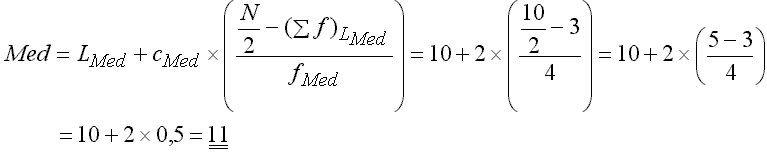
Die Aussage des Medians lautet für die gegebene Verteilung der Wartezeiten: Die Hälfte der Patienten warten mehr als 11 Minuten , die andere Hälfte weniger als 11 Minuten bis zur Behandlung.
Die Ausgangstabelle
![]() Als Aufgabe berechnen Sie den feinberechneten Median für die
nachstehende Verteilung der jährlichen Urlaubsausgaben von
Studierenden:
Als Aufgabe berechnen Sie den feinberechneten Median für die
nachstehende Verteilung der jährlichen Urlaubsausgaben von
Studierenden:
Tabelle 3-6: Urlaubsausgaben von Studierenden
|
Nr. |
von ... EUR |
bis unter ... EUR |
An-zahl |
Klassenmitte |
Klassenbreite |
kum. Hf. |
|
1 |
0 |
250 |
17 |
125 |
250 |
17 |
|
2 |
250 |
450 |
14 |
350 |
200 |
31 |
|
3 |
450 |
550 |
9 |
500 |
100 |
40 |
|
4 |
550 |
650 |
15 |
600 |
100 |
55 |
|
5 |
650 |
750 |
13 |
700 |
100 |
68 |
|
6 |
750 |
850 |
9 |
800 |
100 |
77 |
|
7 |
850 |
1150 |
14 |
1000 |
300 |
91 |
|
8 |
1150 |
2150 |
5 |
1650 |
1000 |
96 |
|
9 |
2150 |
3350 |
4 |
2750 |
1200 |
100 |
|
Summe: |
100 |
|
||||