| Druckversion: | Nach dem Drucken: | und zurück zum Dokument |
Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken
| ViLeS 1 > III Maße der zentralen Tendenz (Mittelwerte) > III-2 Der Median > Konzept und Definition |
Der Median (Med) teilt eine geordnete Reihe von
Beobachtungen in zwei gleich große Teile. 50% der Beobachtungen
liegen unter dem Median, die restlichen 50% über dem Median. Er
stellt also im wahrsten Sinne des Wortes einen "Durchschnitt"
dar.
Damit eine Beobachtungsreihe geordnet werden kann, muss das Merkmal mindestens ordinal-skaliert sein.
Liegen ordinale oder metrische Messwerte vor, so müssen diese zunächst der Größe nach sortiert werden. Danach lässt sich der Median sehr leicht bestimmen.
In der
Reihe: 2, 3, 3, 4, 4, 5, 6, 7, 8, 8, 9
entspricht der Median dem Messwert 5. Bei insgesamt n=11 Werten
liegen genau fünf Werte über und fünf unter 5. Bei
einem ungeraden n ist der Median deshalb ein tatsächlicher Wert.
Bei einem geraden n ist der Median das arithmetische Mittel zweier
benachbarter Messwerte. Die Messwertreihe 3, 4, 4, 5, 6,7,
8, 8, 9, 9 führt zu einem Median von (6 + 7) / 2 =
6,5.
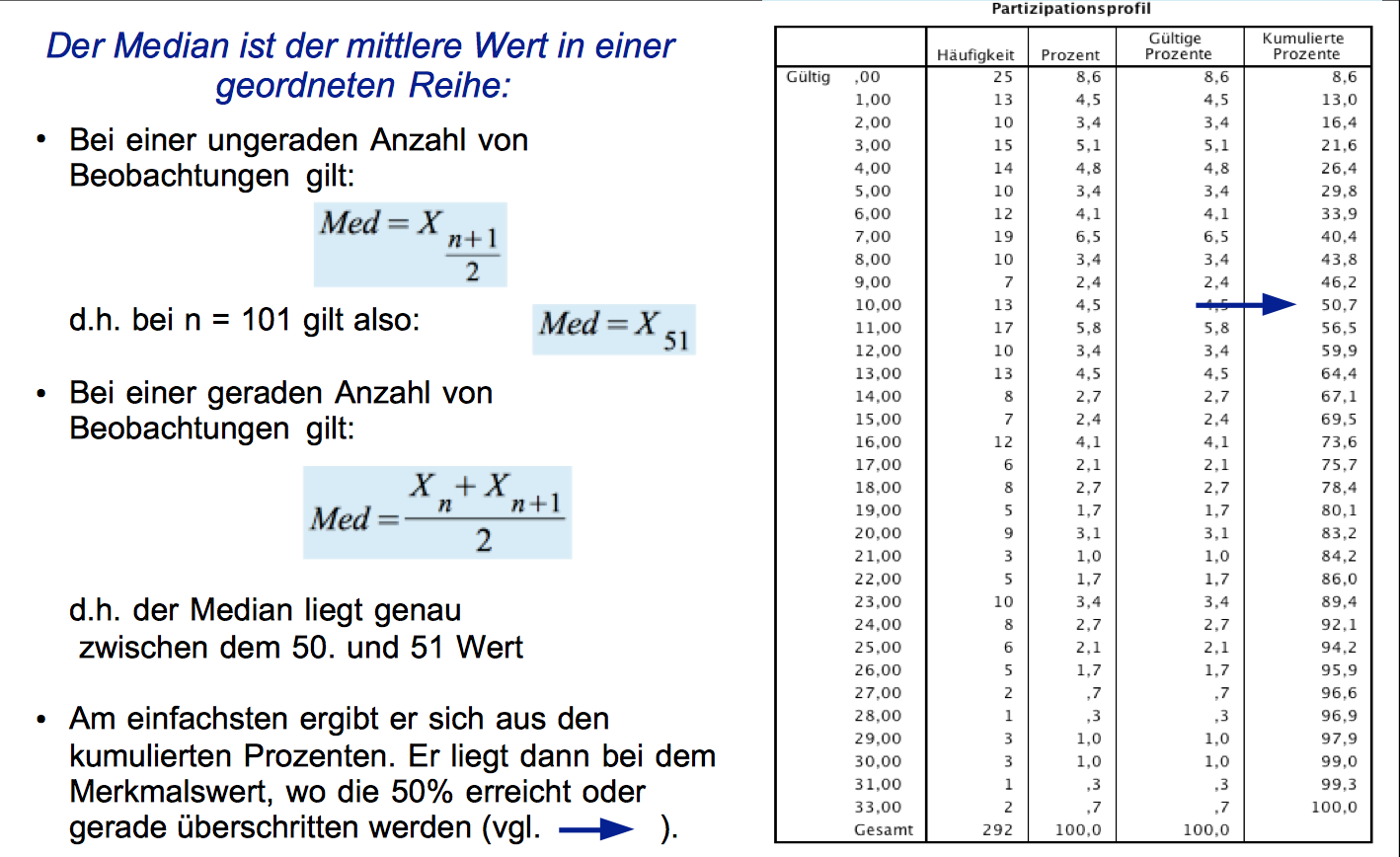
Eine formelmäßige Darstellung des Medians einer geordneten Reihe findet sich auf der linken Hälfte der Abb 3-6.
Bei umfangreicheren Tabellen, wie auf der rechten Seite der nachfolgenden Abb. 3-6, greift man am besten auf die kumulierten Häufigkeiten zurück und bestimmt die Merkmalsausprägung als Median, bei der die 50%-Marke erreicht oder gerade überschritten wird.
Abbildung 3-6: Ermittlung des Medians aus der Häufigkeitsverteilung

Etwas aufwändiger ist die näherungsweise Ermittlung des feinberechneten Medians für klassiertes Datenmaterial. Deshalb und weil der Wert aus nicht-klassierten Daten genau ist, sollte dieser, wenn möglich, vorgezogen werden.
Zur rechnerischen Ermittlung aus der Tabelle ist zuerst die
mediane Klasse zu bestimmen. Dies ist jene Klasse, in welcher die kumulierten Häufigkeiten
![]() den Wert
den Wert
![]() erreicht bzw. überschreitet. Dafür ist es hilfreich, sich in
einer Arbeitstabelle die kumulierten Häufigkeiten zu berechnen.
erreicht bzw. überschreitet. Dafür ist es hilfreich, sich in
einer Arbeitstabelle die kumulierten Häufigkeiten zu berechnen.
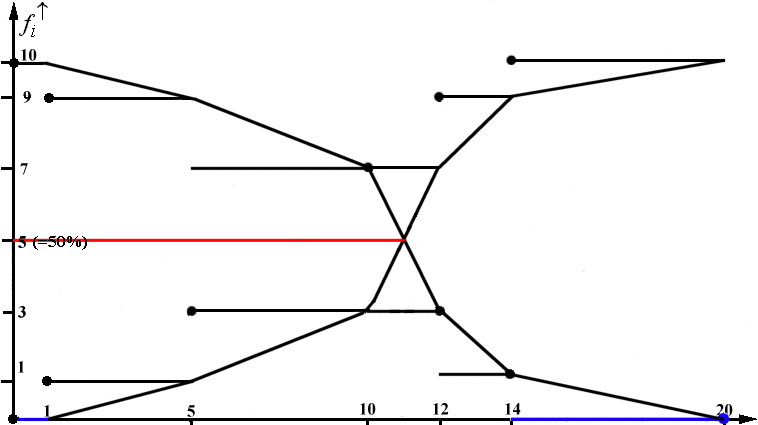
In der folgenden Grafik aus Kap. II-3 sind sowohl die auf- und abwärts kumulierten Häufigkeiten der Wartezeiten in einer Arztpraxis in den auf- wie absteigenden Treppenfunktionen und den entsprechenden Summenpolygonen dargestellt. Der dem Schnittpunkt der Polygone zuzuordnende Merkmalswert ist der Median.
Abbildung 2-11: Auf- und abkumulierte Treppenfunktionen und Summenpolygonen
Die nachstehende Formel für den feinberechneten Median ergibt sich demzufolge wieder aus einem Strahlensatz, der sich aus der graphischen Darstellung der Summenpolygone formulieren lässt (vgl. dazu die Erläuterungen in den weiteren Materialien).
Die Formel für den Median lautet nun:
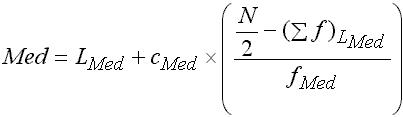
Die einzelnen Ausdrücke in der Formel ergeben sich als:
|
|
Klassenunterrand der medianen Klasse |
|
|
Klassenbreite der medianen Klasse |
|
|
Summe der Häufigkeiten unterhalb der medianen Klasse |
|
|
Häufigkeit in der medianen Klasse |
letzte Änderung am 28.2.2020 um 7:49 Uhr.
Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles1/kapitel03_Mittelwerte/modul02_Der~~lMedian/ebene01_Konzept~~lund~~lDefinition/03__02__01__01.php3