 |
Konzepte und Definitionen im Modul III-1 Der Modus
1. Das Konzept des Modus
Der Modus ist ein einfacher Lagewert. Er bezeichnet den am
häufigsten beobachteten
Merkmals-Wert. Dies setzt zumindest geordnete und gruppierte Daten voraus. Darüber hinaus müssen die Daten mindestens ordinales Skalenniveau aufweisen, denn nur dann kann von einem Zentrum der Verteilung gesprochen werden.
Bei nominalen Daten ist in der Regel auch ein Merkmal mit der größten Häufigkeit gegeben. Da die Reihenfolge der Merkmalsausprägungen aber beliebig ist, kann dann nicht von einem Zentrum gesprochen werden.
2. Der Modus bei nicht-klassierten Daten
Aus gruppiertem Material ist der Modus, die Beobachtung also, die die größte
absolute Häufigkeit fi aufweist, in der Regel sehr leicht zu
bestimmen.
a) Die Ermittlung aus der Häufigkeitstabelle bzw. dem Histogramm
Im Folgenden stützen wir uns auf die bereits bekannte Verteilung der Urlaubsausgaben von Studierenden (vgl. Abb. 3-3). In der Tabelle bzw. im zugehörigen Histogramm weist die Häufigkeit (vgl. dazu die Spalten "Anzahl" der nachstehenden Tabelle) bzw. die Höhe der Säulen auf den Modus hin.
Abbildung 3-3: Tabelle und Graphik der Urlaubsausgaben
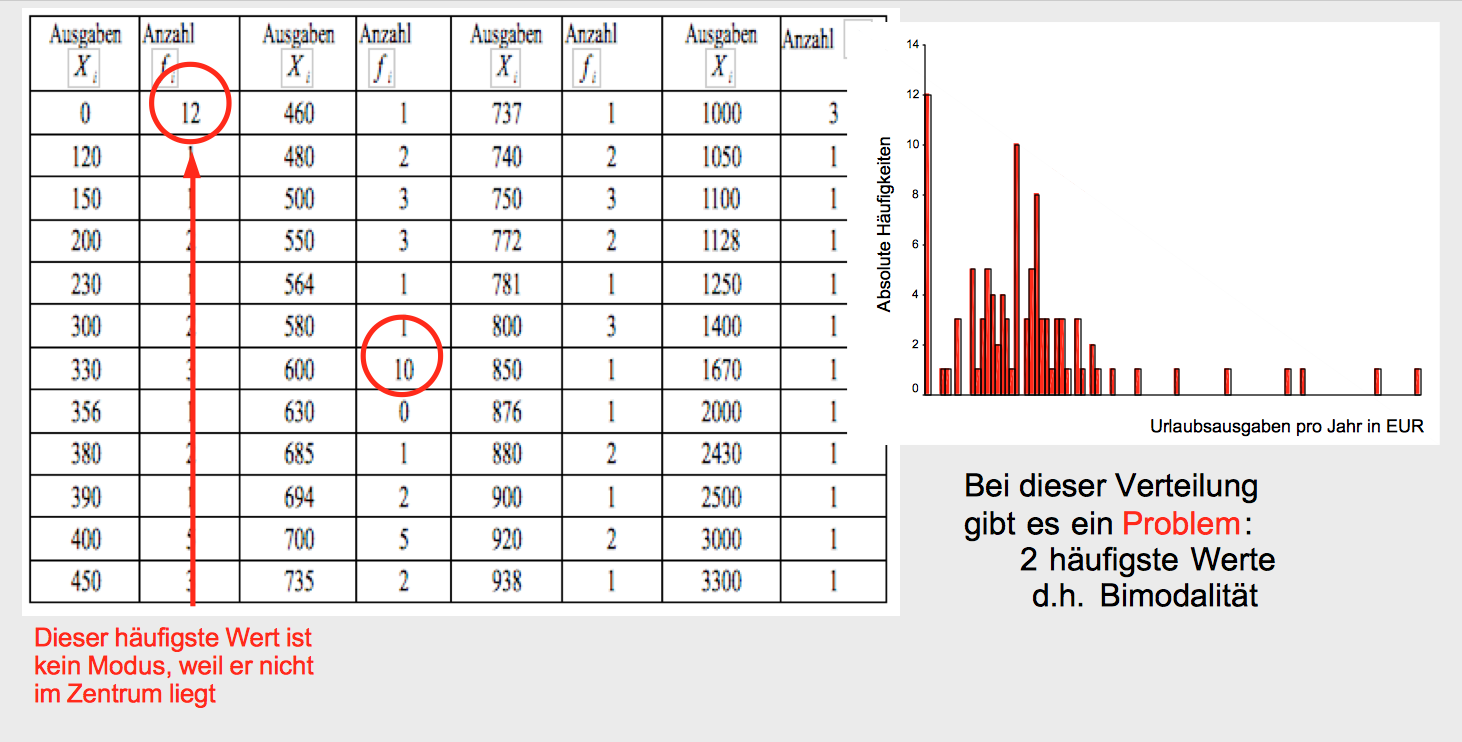
b) Problem bei der Ermittlung des Modus
An diesem Beispiel wird bereits eine zweifache Problematik der modalen Werte deutlich:
-
Zum einen existieren manchmal - wie im Beispiel - Verteilungen mit zwei weit aus einander liegenden Merkmalen mit jeweils vergleichsweise hohen Fallzahlen. Man spricht dann von bimodalen Verteilungen. In der Realität trifft das vor allem dann auf, wenn zwei unterschiedliche Verteilungen gemeinsam dargestellt werden (wie etwa bei der Verteilung der Wochenarbeitszeiten, die für Frauen und Männer in der Regel von einander abweichende Modi aufweist). In Abb. 3-3 sind es zwei unterschiedliche Personengruppen: die, die in Urlaub gefahren und die, die nicht in Urlaub gefahren sind.
Ausserdem sind bisweilen Verteilungen zu finden, bei denen der häufigste Wert (und das Beispiel ist fast ein derartiger Fall) nicht im Zentrum der Verteilung zu finden ist. Auch dann kann natürlich nicht von einem Modus gesprochen werden. Zumindest das letzte Problem lässt sich beheben, wenn man sich auf klassierte Daten stützt, da dort die Zufälligkeit einzelner Merkmalshäufungen in der Klasse aufgefangen wird.
3. Der Modus bei klassierten Daten
a) Das Konzept des feinberechneten Modus
Bei klassierten
Daten muss der Modus annähernd ermittelt werden. Dazu ist zuerst die modale Klasse zu finden, d.h. die am
häufigsten besetzte Klasse. Dabei ist nicht von den einfachen Häufigkeiten sondern von den Häufigkeitsdichten auszugehen.
Bei der Bestimmung eines Näherungswertes für den Modus innerhalb
dieser modalen Klasse wird unterstellt, dass sich die
Häufigkeiten innerhalb der Klasse so verteilen wie die
Häufigkeiten der rechten und linken benachbarten Klasse.
Dies lässt sich graphisch, hier am Beispiel der Wartezeiten in einer Arztpraxis demonstrieren:
Abbildung 3-4: Die geschätzte Verteilung der Merkmalswerte in der Modalklasse
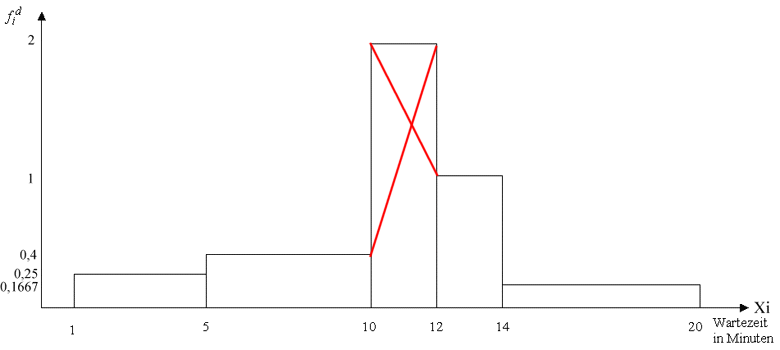
Der feinberechnete Modus ergibt sich dabei aus dem Schnittpunkt der roten Linien als Lot auf die Merkmalsachse.
b) Die Rechenformel für die Ermittlung des Modus
Die nachfolgende Formel lässt unter Verwendung des Strahlensatzes aus der obigen Graphik ableiten (vgl. dazu die Erläuterungen in den weiteren Materialien)
Die Formel für den feinberechneten Modus lautet:
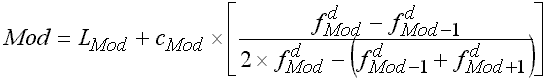
Die einzelnen Ausdrücke in der Formel bedeuten:
|
|
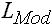
Klassenunterrand der modalen Klasse
|
|
|
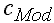
Klassenbreite der modalen Klasse
|
|
|
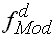
Häufigkeitsdichte der modalen Klasse
|
|
|
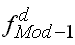
Häufigkeitsdichte der, der modalen Klasse vorhergehenden
Klasse
|
|
|
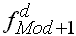
Häufigkeitsdichte der, der modalen Klasse folgenden Klasse
|
Dabei ist die modale Klasse jene Klasse, in welcher sich der
höchste Wert für
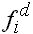befindet.
Wurden die modifizierten Häufigkeitsdichten
berechnet, kann alternativ auch mit diesen
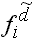gerechnet werden:
|
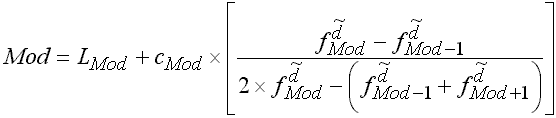
