|
III Statistische Mittelwerte (Maßzahlen der zentralen Tendenz)
- Einleitung und Modulübersicht -
1. Die Funktion statistischer Maßzahlen
Im Kapitel "Statistische Mittelwerte" wird die Diskussion einer numerischen Form von statistischen Modellen eröffnet, die als "Parameter" der Häufigkeitsverteilungen aufgefasst werden können. Diese charakterisieren die Verteilung mit Zahlenwerten. Im Text werden sowohl unterschiedliche Aspekte der Verteilung beschrieben, wie auch verschiedene Optionen der Beschreibung vorgestellt.
Abbildung 3-1: Aufgaben der statistischen Maßzahlen
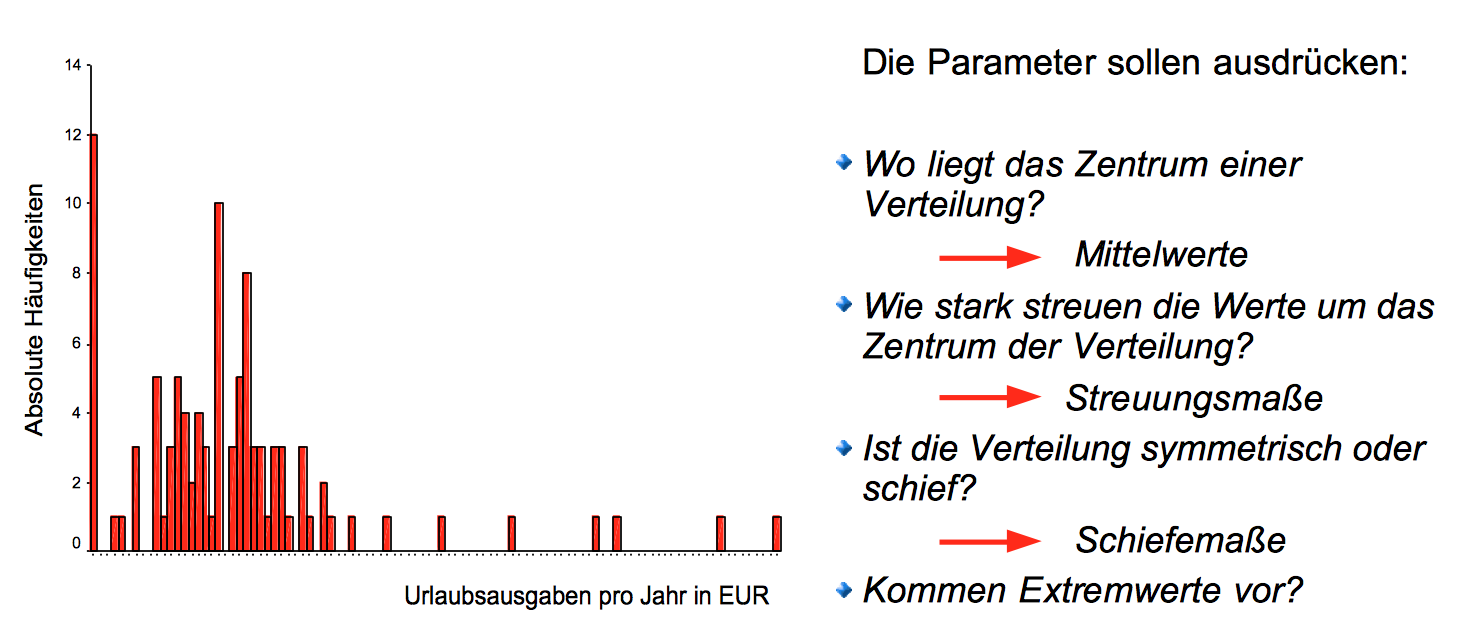
2. Typen von statistischen Mittelwerten
Statistische Mittelwerte verdichten die Informationen zu den Einzelbeobachtungen in einem univariaten Datensatz zu einer oder wenigen Informationen über das Zentrum einer Verteilung. Aus diesem Grund spricht man bei ihnen auch von Maßen der zentralen Tendenz. Dazu stehen verschiedene Ansätze zur Verfügung:
Abbildung 3-2: Lagetypische und rechnerische Mittelwerte
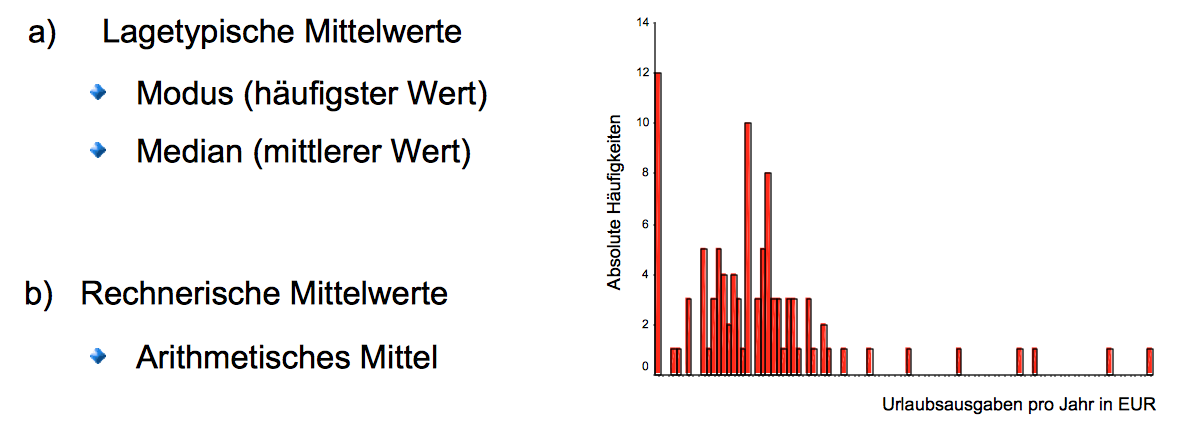
Zu den lagetypischen Maßen zählen
der Modus (häufigster Wert) - dies ist die Merkmalsausprägung mit der größten beobachteten Häufigkeit - und
der Median (Zentralwert). Das ist der Wert, der sich in der Mitte einer geordneten Reihe befindet
Für ihre Ermittlung ist die Lage bestimmter Beobachtungen relevant, so dass nicht alle Werte bei der Ermittlung berücksichtigt werden.
Unter den rechnerischen Mittelwerten ist vor allem
das arithmetische Mittel zu nennen. In
diese Maßzahl gehen alle Beobachtungen ein, was besonders beim Vorliegen von Extremwerten zu Verzerrungen führen kann.
Für eine Reihe von Ausgangsdaten (so vor allem für Verhältniszahlen und Wachstumsraten) ist das arithmetische Mittel nicht geeignet. Auf eine genauere Darstellung der dazu dienlichen rechnerischen Mittelwerte wird hier verzichtet (vgl dazu Litz: Statistische Methoden in den Wirtschafts- und Sozialwissenschaften, 3. Auflage 2003, S.90 ff). Formelhinweise finden sich in den weiteren Materialien
Insofern gilt es auch hier zu prüfen, welcher Mittelwert-Typ geeignet ist, das Zentrum einer Verteilung adäquat zu charakterisieren.
Oft ist es zu raten, alle drei möglichen Maßzahlen in Betracht zu ziehen, um unterschiedliche Aspekte einer Verteilung anzusprechen.
Darüber hinaus spielt bei der Wahl der Maßzahl das Skalenniveau der Daten eine große Rolle.
3. Die Verwendbarkeit statistischer Mittelwerte
Bei der Wahl der Mittelwerte ist zu
berücksichtigen, dass ihre Zulässigkeit an das Skalenniveau der Daten geknüpft ist:
Der Modus kann bei nominalen Skalenniveaus nur
bedingt verwendet werden.
Seine Aussage "die meisten Beobachtungen fallen auf ..."
ist zwar auch hier zutreffend, wie z.B. beim Merkmal "Familienstand" bezüglich der Ausprägung "verheiratet". Da die Reihenfolge nominaler
Ausprägungen jedoch beliebig ist, hat der Modus nicht mehr den
Status eines Mittelwertes.
Der Median bezeichnet die Mitte einer geordneten Reihe. Dies setzt zumindest ein ordinales Skalenniveau der Daten voraus.
Beim arithmetischen Mittel werden
die Merkmalswerte addiert, was nur bei metrischen
Daten zulässig ist. Also scheidet dieses Maß für nominal- und ordinalskalierte
Daten aus.
Diese Einschränkungen sind in dem folgenden Überblick zusammengefasst:
Tabelle 3-1: Mittelwerte und Skalenniveau
|
Mittelwert
|
|
Skalen-niveau
|
Modus
|
Median
|
arithmetisches Mittel
|
|
nominal
|
(x)
|
-
|
-
|
|
ordinal
|
x
|
x
|
-
|
|
metrisch
|
x
|
x
|
x
|
4. Modulüberblick
In den folgenden Abschnitten werden:
die graphische und rechnerische Ermittlung und die Interpretation der Ergebnisse der verschiedenen Modellansätze vorgestellt.
-
Unter dem Punkt „Mittelwerte in der Praxis" wird auf die Vergleichbarkeit ihrer Aussage sowie auf das Problem der Ausreißer eingegangen werden.
-
Das Modul "Eigene Analysen" behandelt die Berechnung statistischer Mittelwerte mit SPSS und die Durchführung empirischer Untersuchungen anhand konkreter Datensätze sowie die Interpretation und Diskussion deren Ergebnisse.
Das Kapitel beinhaltet demnach die folgenden Module:
Wählen Sie ein Modul: - III-1 Der Modus
- III-2 Der Median
- III-3 Das arithmetische Mittel
- III-4 Mittelwerte in der Praxis
- III-5 Eigene Analysen und Interpretationen
| 


