| Druckversion: | Nach dem Drucken: | und zurück zum Dokument |
Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken
| ViLeS 1 > II Tabellarische und graphische Aufbereitung eindimensionaler statistischer Daten > II-4 Die tabellarische Darstellung klassierter Daten > Beispiele und Aufgaben |
Das Problem der Klassierung soll an Hand der fiktiven Urlaubsausgaben Oldenburger Studierender (vgl. Tab. 2-7) verdeutlicht werden. Diese Tabelle besteht noch aus 48 Zeilen. Wie man aus dem zugehörigen Histogramm (Abb. 2-8) erkennen kann, sind gerade die oberen Merkmalswerte nur vereinzelt besetzt.
Abbildung 2-8: Histogramm der Urlaubsausgaben

Würde man sich bei unserem Beispiel für eine einheitliche Klassenbreiten von 100 entscheiden, entstünden 34 Klassen. Eine Klassenbreite von 500 € ergäbe sieben Klassen.
Anstatt die Grenzwerte in eine oder zwei größere Klassen zusammenzufassen, gäbe es auch die Möglichkeit mit offenen Klassen zu arbeiten. So könnte die letzte z.B. "1100 € und mehr" bzw. die erste "unter 200 €" lauten.
Darüber hinaus sind deutlich Häufungspunkte bei 400 €, 630 € usw. auszumachen.
|
|
Überlegen Sie anhand des Histogramms wie Sie die Daten der Urlaubsausgaben Oldenburger Studierender klassieren würden. Probieren Sie mehrere Möglichkeiten und diskutieren Sie, welche Vor- und Nachteile die gewählten Optionen bei der Klassenbildung bringen. |
Zu dieser Tabelle schlagen wir als Lösungsbeispiel folgende Klassierung vor:
Es wurden neun Klassen gebildet, wobei die untere Klasse eine Klassenbreite von 250 €, die darauffolgende eine von 200 € und die Klassen im Zentrum der Verteilung eine Klassenbreite von 100 € aufweisen.
Die oberen Klassen haben dann wieder eine zunehmend größere Spannweite.
Die Klassierung ergab folgendes Resultat:
Tabelle 2-15: Klassierung der Urlaubsausgaben Oldenburger Studierender
|
Nr. |
von ... € |
bis unter ... € |
Anzahl |
|
1 |
0 |
250 |
17 |
|
2 |
250 |
450 |
14 |
|
3 |
450 |
550 |
9 |
|
4 |
550 |
650 |
15 |
|
5 |
650 |
750 |
13 |
|
6 |
750 |
850 |
9 |
|
7 |
850 |
1150 |
14 |
|
8 |
1150 |
2150 |
5 |
|
9 |
2150 |
3350 |
4 |
|
Summe: |
100 | ||
Gerade bei der Klassierung wird der Modellcharakter der statistische Auswertung besonders deutlich. Außer den genannten Fehlern falscher Klassenbildung und falscher Berechnungen gibt es das Problem der Wahl eines den Daten adäquaten Klassierungsmodells. Diesbezüglich gibt es nicht mehr ein „richtig“ oder „falsch“ sondern nur ein mehr oder minder „adäquat“ und „inadäquat“
|
|
Diskutieren Sie also die vorgeschlagene Lösung und zeigen Sie Verbesserungen oder Erweiterungen auf. |
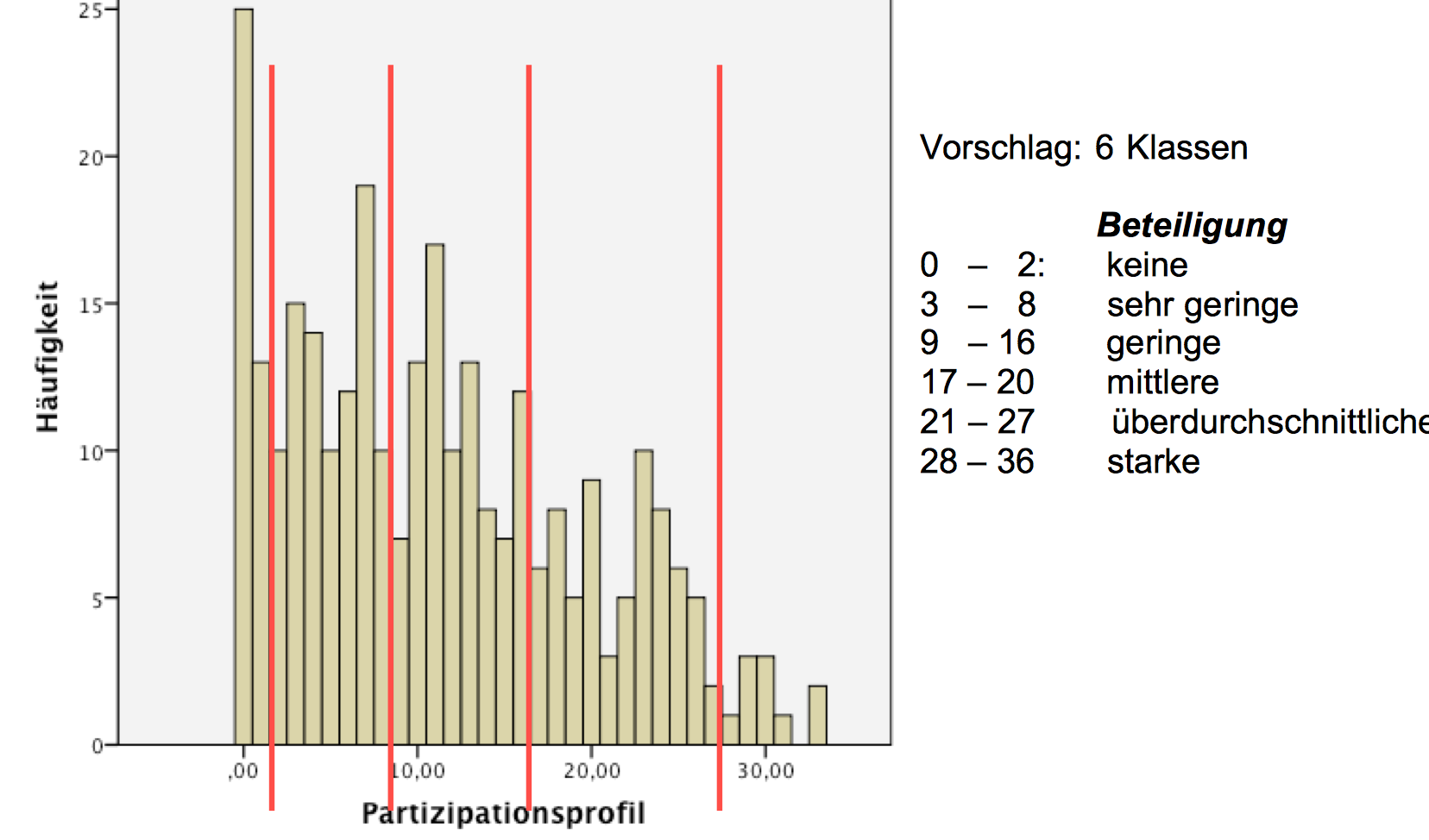
Als Beispiel für eine Klassierung mit SPSS soll die Häufigkeitsverteilung der Variable Partizipationsprofil aus dem Datensatz Partizipation_1.sav dienen. Im Histogramm der Verteilung sind Orientierungslinien markiert, die Segmente definieren, in denen stärker besetzte Merkmalsausprägungen soweit wie möglich im Zentrum der jeweiligen Klasse liegen.
Screenshot 2-25: Strukturiertes Histogramm des Partizipationsprofils
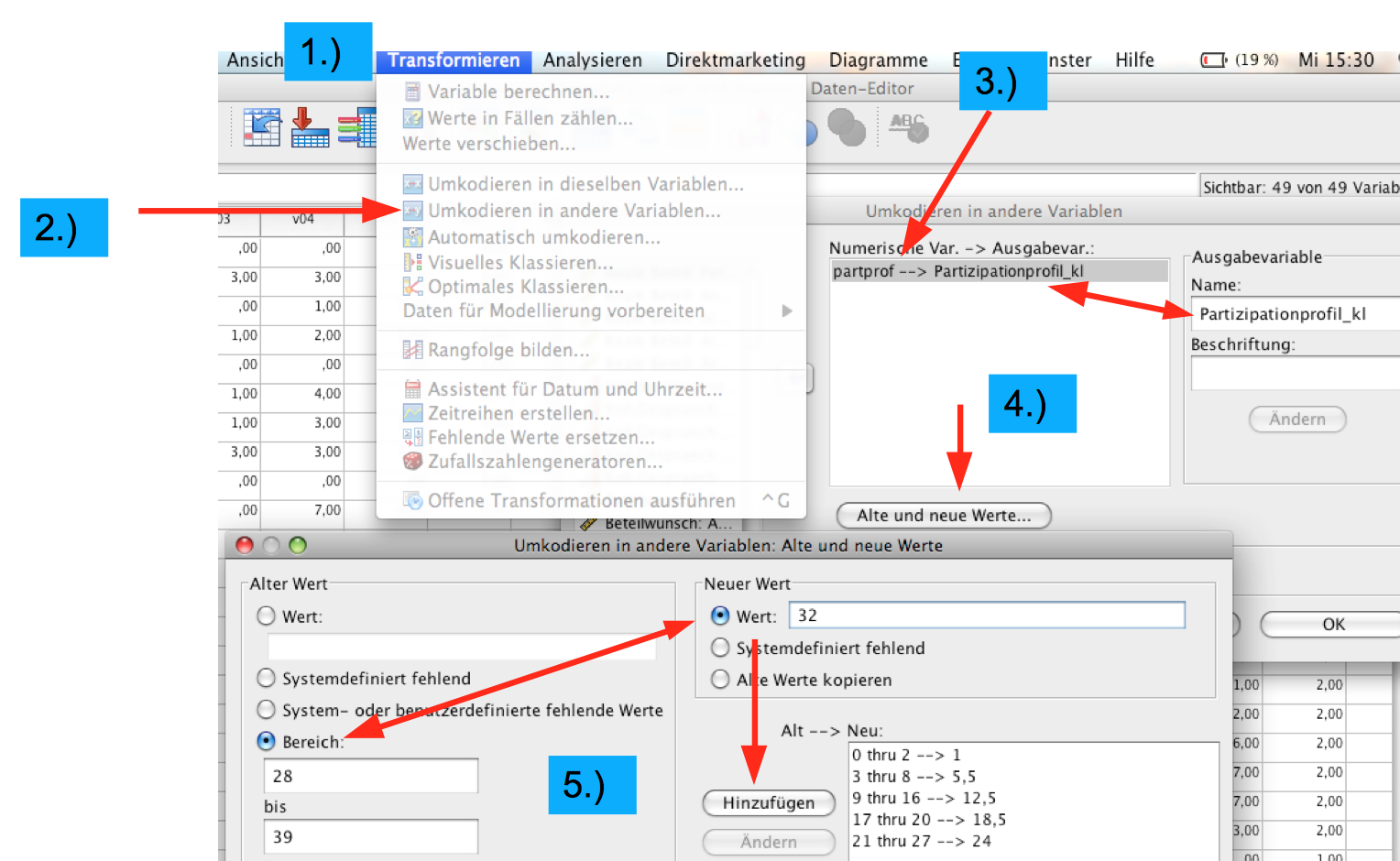
Mit der folgenden Prozedur wird nach diesem Strukturkonzept eine neue Variable "Partizipationsprofil_kl" erzeugt und abgespeichert.
Screenshot 2-26: Klassierung des Partizipationsprofils
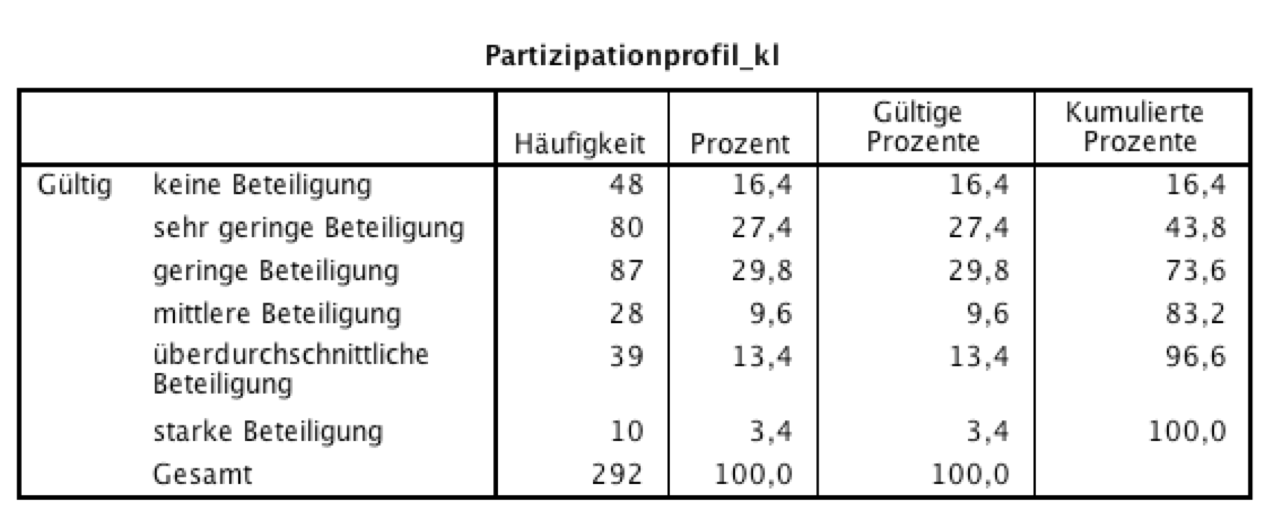
Damit ist eine Variable entstanden, die wie nachfolgende Tabelle - nach Eingabe der Kategorien in der Variablenansicht des Datenblattes - zeigt, die Beteiligung an betrieblichen Entscheidungsprozessen unmittelbar nachvollziehbar macht.
Screenshot 2-27: Häufigkeitstabelle des klassierten Partizipationsprofils
Als Beispiel für die Bestimmung der Häufigkeitsdichte soll eine fiktive Tabelle der Verweildauer der Kundschaft in einem Supermarkt herangezogen werden. Die klassierte Ausgangstabelle wurde um je eine Spalte zur Häufigkeitsdichte und zur modifizierten Häufigkeitsdichte erweitert:
Tabelle 2-16: Berechnung der Häufigkeitsdichte und der modifizierten Häufigkeitsdichte
|
Verweildauer der Kunden in Minuten |
absolute Anzahl |
Klassen-breite |
Hf.-Dichte |
Mod.Hf.-Dichte | |
|
von .... |
bis unter..... |
|
|
|
|
|
0 |
10 |
10 |
10 |
1 |
5 |
|
10 |
15 |
25 |
5 |
5 |
25 |
|
15 |
20 |
22 |
5 |
4,4 |
22 |
|
20 |
30 |
17 |
10 |
1,7 |
8,5 |
|
30 |
45 |
3 |
15 |
0,2 |
1 |
Als Normklassenbreite wurde mit ![]() die der
mittleren Klassen gewählt, was einerseits fast überall zu glatten Werten für die
modifizierte Häufigkeitsdichte führt und sie andererseits im Bereich der
mittleren Verweildauern den absoluten Häufigkeiten angleicht.
die der
mittleren Klassen gewählt, was einerseits fast überall zu glatten Werten für die
modifizierte Häufigkeitsdichte führt und sie andererseits im Bereich der
mittleren Verweildauern den absoluten Häufigkeiten angleicht.
Berechnen Sie zur klassierten Verteilung der Urlaubsausgaben Oldenburger Studierender die Klassenbreiten ci und Klassenmitten
mi und tragen Sie in jedes Feld den entsprechenden Wert ein.
Sind Sie fertig, klicken Sie auf OK.
Tabelle 2-17: Berechnung der Klassenmitten der klassierten Urlaubsausgaben
Berechnen Sie nun weiter die Häufigkeitsdichte für die klassierte Verteilung der Urlaubsausgaben Oldenburger Studierender.
Bitte beachten Sie:
Runden Sie Ihre Ergebnisse auf 4 Nachkommastellen!
Schreiben Sie ein Komma als Punkt!
Sind Sie fertig, klicken Sie auf OK.
Tabelle 2-18: Berechnung der Häufigkeitsdichten der klassierten Urlaubsausgaben
Wenn Sie für eine vorgebene Häufigkeitstabelle Auswertungen vornehmen möchten - hier z.B. die Berechnung der Häufigkeitsdichen - können Sie das nachfolgend verlinkte Rechenprogramm einsetzen.
Dazu tragen Sie Ihre Tabellenwerte in eine Eingabe-Tabelle ein und starten das Tool.
Tabelle 2-19: Vorschau auf die Eingabetabelle

Hier können Sie das integrierte Programm Häufigkeitstabellen aufrufen.
letzte Änderung am 28.2.2020 um 7:49 Uhr.
Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles1/kapitel02_Tabellarische~~lund~~lgraphische~~lAufbereitung~~lstatistischer~~lDaten/modul04_Die~~lH~~aeufigkeitsdicht
e/ebene02_Beispiele~~lund~~lAufgaben/02__04__02__01.php3