 |
Konzepte und Definitionen im Modul II-4 Die tabellarische Darstellung klassierter Daten
1. Vorbemerkungen
a) Die
Klassierung der statistischen Daten: Vorzüge und Fallstricke
Wie die nachstehende Tabelle der Urlaubsausgaben aus Kap. II-2 zeigt, reicht in vielen Fällen die durch Gruppierung vorgenommene Reduktion des
Tabellenumfangs nicht aus, die gegebenen Informationen
schnell und substantiell aufzunehmen.
Tabelle 2-7: Häufigkeiten der Urlaubsausgaben
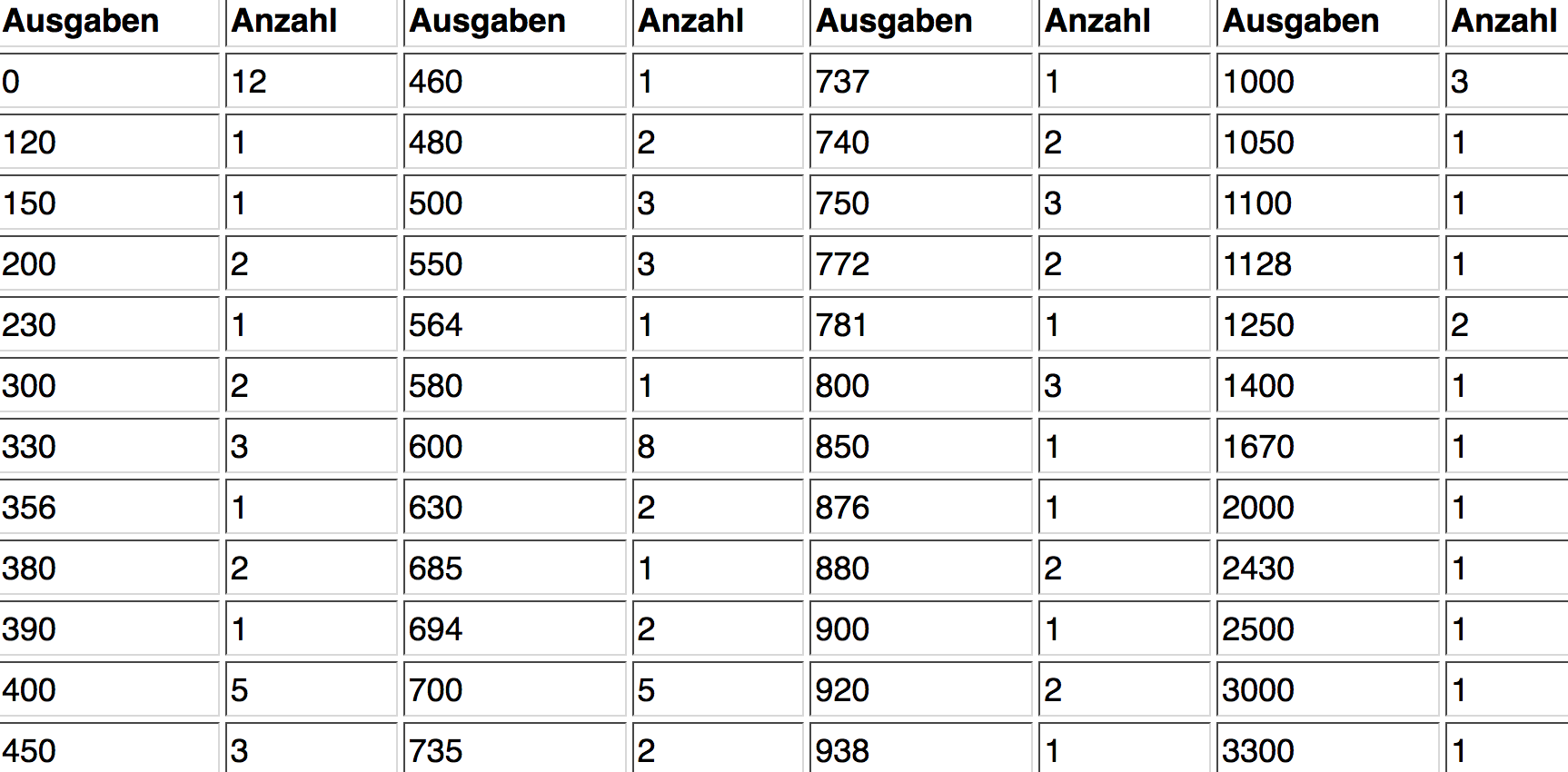
Deshalb sollen
in den folgenden Aufbereitungsschritten
die gruppierten Daten nochmals verdichtet werden. Dazu bedient man sich der
Klassierung, bei der die Merkmalsausprägungen in Klassen zusammengefasst werden.
Bei der Klassierung ist zu beachten, dass die Unterschiede in
den Merkmalsausprägungen innerhalb der Klassen nivelliert werden, so dass relevante Informationen über die
einzelnen Merkmalsausprägungen verloren gehen. Darüber hinaus kann durch die Festlegung der Klassen die Verteilungsstruktur der Daten, wie sie in dem entsprechenden Histogramm (vgl. Abb. 2-8 aus Kap. II-3) zum Ausdruck kommt, verwischt werden.
Abbildung 2-8: Histogramm der Urlaubsausgaben
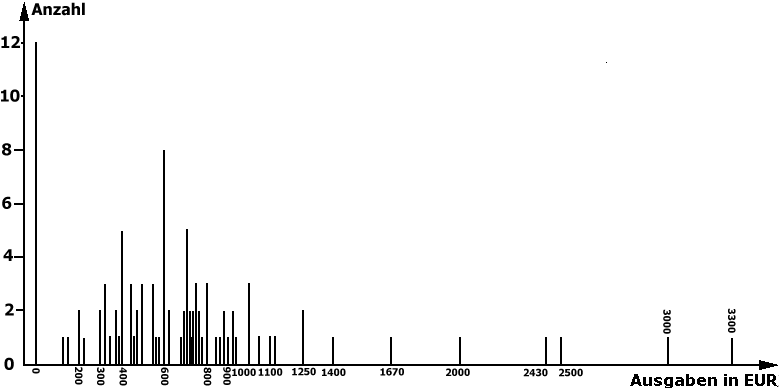
Deshalb gilt es bei der
Klassierung eine ausgewogene Balance zwischen dem Informationsverlust, dem
Gewinn an Anschaulichkeit und der Bewahrung der Verteilungsstruktur zu finden.
a) Möglichkeiten der Klassierung der statistischen Daten
Unter diesem Aspekt soll in den folgenden Abschnitten diskutiert werden,
wie die gruppierten Daten der Urlaubsausgaben in Klassen eingeteilt werden können. Dabei ist zu klären:
-
die Festlegung der
Klassengrenzen,
-
die Anzahl der Klassen (10 bis 15 Klassen),
-
einheitliche oder
unterschiedliche Klassenbreiten,
-
offene oder geschlossene
Klassen und
-
die Zentrierung der Klassen
(Festlegung der Klassenmitten).
2. Die Optionen der Klassenbildung
a) Die Festlegung der
Klassengrenzen
Wichtigstes Kriterium beim Setzen von
Klassengrenzen ist, dass sich diese nicht überschneiden dürfen. Jede
Klasse muss eindeutig abgegrenzt sein. Dies betrifft:
-
die Definition der Klassenuntergrenze 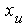 , ,
-
die Definition der Klassenobergrenze 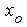 und somit und somit
-
die Festlegung der Häufigkeit der in dieser Klasse
befindlichen Beobachtungen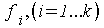
Da sich z.B. die Klassen "0 bis 500 €" und
"350 bis 700 €" überschneiden, wäre diese Einteilung nicht erlaubt! Ebenso
wenig wären die Klassen "0 bis 350 €" und "350 bis 700 €" eindeutig, da
Ausgaben in Höhe von 350 € beiden Klassen zugeteilt werden könnten.
Im Prinzip gibt es zwei Möglichkeiten einer
eindeutigen Grenzziehung:
a) "mehr als... bis einschließlich ..." und
b) "von
... bis unter ...",
die beide hinsichtlich der Eindeutigkeit gleichwertig sind (vgl. dazu aber auch Punkt d. zur Wahl der Klassenmitte). So lauten die o.a. Klassen
exakt: "von 0 bis unter 350 €" und "von 350 bis unter 700 €". Die
Eindeutigkeit ist somit hergestellt. In jeder der so definierten Klassen wird
die Anzahl bzw. die Häufigkeit der in sie fallenden Beobachtungen
eingetragen.
Wir entscheiden uns für die folgende Konvention:
|

|
Klassen werden im folgenden immer in dem Format "von ... bis unter ..."
definiert und gelesen. |
b) Die Festlegung der Anzahl der
Klassen
In den Extremfällen könnte eine einzige Klasse gebildet werden,
in der sich alle Beobachtungen wiederfinden, oder so viele Klassen, dass jede
Klasse die Beobachtungen der gruppierten Daten aufweist. Beide Modelle sind
unter den obigen Zielsetzungen nicht sinnvoll. Durch die Klassierung sollen die
Daten übersichtlicher gestaltet werden. Mehr als 8 - 10 Klassen sollten also die
Ausnahme darstellen. Die endgültige Wahl der Anzahl muss jedoch auch die
folgenden Aspekte einschließen.
c) Die Gestaltung der
Klassenbreiten
Die Bei der Wahl der Klassenbreite gibt es zwei Optionen:
Grundsätzlich
gilt, dass einheitliche Klassenbreiten die Lesbarkeit einer Tabelle erhöhen, da
der Leser neben den Häufigkeiten einer Klasse nicht auch noch deren Breiten im Auge behalten muss. Ausserdem ist bei einheitlicher Klassenbreite
durch die Festlegung der Anzahl der Klassen diese eigentlich mit bestimmt. Im Analyseprogramm SPSS wird deshalb mit konstanten Klassenbreiten gearbeitet.
Unterschiedliche Klassenbreiten sind aber in
vielen Fällen sinnvoller. Bei einer Konzentration der Daten in einem mittleren
Bereich und einer breiten Streuung an den Rändern empfiehlt es sich, im Zentrum
mit einer geringeren, dann aber möglichst einheitlichen Klassenbreite zu
arbeiten und an den Rändern mit einer größeren Klassenbreite. Allerdings zwingen sie den Leser bei der Interpretation der klassierten Häufigkeiten, diese auf die Klassenbreite zu beziehen,
Oft ist es ist auch angebracht zu den geschlossenen Klassen im Zentrum
der Verteilung die Beobachtungen in offenen Klassen an den Rändern zusammenzufassen.
Diese Option ist zunächst sehr angenehm, erschwert aber u.U. die graphische
Darstellung und die Berechnungen von Mittelwerten und Streuungsmaßen.
d) Die Festlegung der
Klassenmitten
Wenn es um sehr differenzierte Daten geht, die zudem auch eher als ungefähre
Angaben ermittelt wurden, so z.B: Angaben zum Einkommen, zur Miete etc., ist
eine Zentrierung der Klassenmitten auf die Häufungspunkte sinnvoll. Viele
Befragte werden z.B. ihr Einkommen oder ihre Urlaubsausgaben eher auf volle hundert € Beträge auf- bzw.
abrunden, als den exakten Betrag in Euro und Cent anzugeben (vgl. dazu z.B. das obige Diagramm). So kann es
hier und im allgemeinen sinnvoll sein, einen runden Hunderterbetrag wie z.B. den
Betrag von 400 € in die Mitte einer Klassen zu legen ("350 bis unter 450
€").
Dieses Vorgehen hat einen weiteren Vorteil: da der Ausschuss oder die
Einbeziehung der Obergrenzen einer Konvention "bis unter ..." folgt, könnte es
bei einer Änderung der Konvention unangebrachte Verschiebungen geben. Probanden,
die "300 €" angaben, fänden sich einmal in der Klasse "von 300 bis unter 400
€", das andere Mal in der Klasse "mehr als 200 bis einschließlich 300 €"
wieder: Das Bild wäre dann ein ganz anderes.
3. Die Berechnung der Klassenmitten und der Häufigkeitsdichten
Zur Ermittlung von statistischen Maßzahlen aber auch zur graphischen Darstellung der klassierten
Häufigkeitstabelle ist eine weitere Bearbeitung der Informationen dieser
Verteilung notwendig. Es ist dabei sinnvoll mit einer Arbeitstabelle zu
arbeiten, insbesondere wenn ungleiche Klassenbreiten oder offene Klassen
verwendet wurden.
Die Tabelle der klassierten Daten soll dann um zwei
Spalten zur expliziten Information über die in ihr zugrunde gelegten
Klassenmitten und -breiten erweitert werden.
Wird in der klassierten Häufigkeitstabelle mit
ungleichen Klassenbreiten gearbeitet, so ist nicht mehr ausschließlich die
absolute Häufigkeit interessant, sondern ebenso die sog.
Häufigkeitsdichte, d.h. die Relativierung der Häufigkeit durch die Klassenbreite. Sie wird für die grafische Darstellung der Verteilung
in einem Histogramm und die Berechnung des Modus benötigt.
Der Sinn und Zweck der Häufigkeitsdichte besteht
bei ungleichen Klassenbreiten darin, die ermittelten Häufigkeiten durch die
jeweiligen Klassenbreiten zu relativieren. Unterschiedliche Klassenbreiten
bringen das Problem mit sich, dass mit wachsender Breite der Klasse mehr
Merkmalsträger zu erwarten sind. (Die Breite der Klasse spielt für eine
Häufigkeitsverteilung eine ebenso wichtige Rolle wie die Anzahl der Quadratmeter
für den Grundpreis einer Wohnung. Für die Preiswürdigkeit einer Wohnung ist der
Preis pro Quadratmeter u.U. relevanter als der Gesamtpreis. )
Liegen unterschiedliche Klassenbreiten vor, muss mit Häufigkeitsdichten
gearbeitet werden! Sie wird wie folgt berechnet:
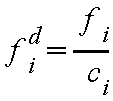
Die modifizierte Häufigkeitsdichte 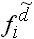 (sprich: f i d - Schlange)wird verwendet, um einige oder alle Werte der
Häufigkeitsdichten einer Tabelle runder zu machen und möglichst viele
(die zentralen Häufigkeitsdichten) an die absoluten Häufigkeiten anzupassen.
Hierzu werden alle Häufigkeitsdichten mit einem Proportionalitätsfaktor
(sprich: f i d - Schlange)wird verwendet, um einige oder alle Werte der
Häufigkeitsdichten einer Tabelle runder zu machen und möglichst viele
(die zentralen Häufigkeitsdichten) an die absoluten Häufigkeiten anzupassen.
Hierzu werden alle Häufigkeitsdichten mit einem Proportionalitätsfaktor 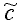 multipliziert. Generell kann multipliziert. Generell kann
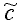 beliebig gewählt werden, zwei
Hinweise seien jedoch gegeben. beliebig gewählt werden, zwei
Hinweise seien jedoch gegeben.
-
Der Wert für 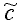 sollte einer
Klassenbreite entsprechen, welche im Zentrum der Verteilung liegt und relativ
häufig vorkommt ("Normklassenbreite oder zentrale Klassenbreite"). sollte einer
Klassenbreite entsprechen, welche im Zentrum der Verteilung liegt und relativ
häufig vorkommt ("Normklassenbreite oder zentrale Klassenbreite").
-
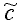 kann auch so gewählt werden,
dass sich für kann auch so gewählt werden,
dass sich für 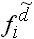 runde Werte
ergeben. runde Werte
ergeben.
Die modifizierte Häufigkeitsdichte 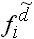 errechnet sich
nach der Formel: errechnet sich
nach der Formel:
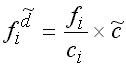
bzw., wenn 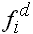 bekannt ist, durch bekannt ist, durch
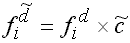
|



