Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken

1. Vorbemerkungen

a) Funktion und Vorbedingungen graphischer Präsentationen

• Wie bereits am Beispiel der Bevölkerungspyramiden verdeutlicht werden konnte, sollen die statistischen Diagramme reale Strukturen bildhaft modellieren.

• Graphische Darstellungen haben dabei den großen Vorteil, dass die Struktur einer empirisch-statistischen Verteilung auf "einen Blick" sichtbar wird - vgl. dazu ebenfalls die Darstellung der Bevölkerungspyramiden in Kap. I.

• Allerdings sind die quantitativen Informationen, meist solche über die Häufigkeiten der Merkmalsausprägungen, optisch nicht exakt zu erfassen. Deshalb ist die graphische Darstellung vor allem als Ergänzung zur bzw. als Veranschaulichung der tabellarischen Darstellung sinnvoll.

• Bei der Erstellung der Graphik ist streng darauf zu achten, dass diese quantitativen Dimensionen des Merkmals exakt in der Graphik wiedergegeben werden. Dies geschieht je nach graphischer Form durch Länge einer Strecke oder das Volumen eines Körpers. Man spricht dann von längenadäquat bzw. von flächenadäquat eines graphischen Elements.

• Die graphische Umsetzung einer Merkmalsverteilung nimmt auf zwei numerische Größen Bezug: auf die Codeziffer der Merkmalsausprägung und auf die dieser Ausprägung zugeordnete Häufigkeit.
  
  Graphische Darstellungen sind in der Regel flächig, oft also in einem zweidimensionalen Koordinatensystem enthalten. Deshalb ist es sehr wichtig, zu klären, ob das dargestellte Merkmal die metrischen Eigenschaften beider Achsen des Koordinatensystems aufweist.

• Aus dem Modul zum Skalenniveau (vgl. Kap I, Modul 2) ist bekannt, dass nominale Skalen weder eine Metrik noch eine Ordnungsrelation aufweisen. Für Daten dieser Art sind Darstellungen im Koordinatensystem nicht zulässig. Für ordinale Skalen ist eine Darstellung im Koordinatensystem nur bedingt geeignet. Nur für metrische Daten können Merkmalsausprägungen und Häufigkeiten jeweils einer Achse adäquat zugeordnet werden.

• Aus den letzen Ausführungen ist zu folgern, dass die Wahl einer graphischen Form primär vom Skalenniveau des Merkmals abhängt.

b) Überblick über die Formen graphischer Präsentationen

Während die Anzahl unterschiedlicher Formen tabellarischer Darstellungen relativ überschaubar ist, gibt es bei den graphischen Präsentationen statistischer Sachverhalt eine Vielzahl von Möglichkeiten, den speziellen Datenstrukturen Ausdruck zu verleihen. Es gibt sogar eine besondere Tradition der "Bildstatistik" .
Im Folgenden sollen deshalb hier nur die vier, für eindimensionale Häufigkeitsverteilungen gebräuchlichsten Diagramme vorgestellt werden:

• das Kreis- oder Tortendiagramm,

• das Liniendiagramm,

• das Stab- oder Säulendiagramm und

• das Histogramm.

Abbildung 2-5: Formen der statistischen Graphiken

Das Histogramm und der Polygonzug werden erst vorgestellt, wenn der Aspekt der Klassierung von Häufigkeitsverteilungen behandelt wurde. Spezielle Formen für kumulierte Daten wie die Treppenfunktion und das Summenpolygon werden am Ende des Moduls präsentiert.

2. Die graphischen Formen der Darstellung

a) Die graphische Darstellung nominal-skalierter Merkmale

Für qualitative - vor allem für nominal-skalierte – Daten ist das Kreisdiagramm die bevorzugte graphische Darstellungsform. Dabei sollte allerdings die Anzahl der Merkmalsausprägungen nicht zu groß sein.

Im Diagramm wird eine Kreisfläche entsprechend den Merkmalshäufigkeiten in Segmente aufgeteilt. Die Häufigkeiten werden flächenadäquat über die Bestimmung des Winkel des Kreissegmentes umgesetzt. Dieser Winkel α_i ergibt sich proportional zum Anteilswert f_i der Merkmalsausprägung X_i :

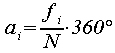
Abbildung 2-6: Allgemeine Form eines Kreisdiagramms

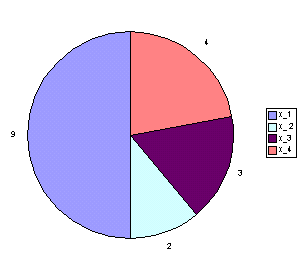
Zur besseren Verständlichkeit empfiehlt es sich, in die Segmente die absoluten oder die prozentualen Häufigkeiten der Merkmalsausprägung einzutragen.

b) Die graphische Darstellung ordinal-skalierter Merkmale

Für quantitative Daten wird i.A. das Stabdiagramm gewählt. Es weist auf der X-Achse die Merkmalswerteund auf der Y-Achse die Merkmalshäufigkeitenaus. Bei einigen statistischen Analyseprogrammen wird allerdings beim Stabdiagramm keine metrische Qualität der Daten unterstellt. Die Stäbe werden also unabhängig von ihren Merkmalswerten unmittelbar aneinander gereiht.

Abbildung 2-7: Allgemeine Form des Stabdiagramms

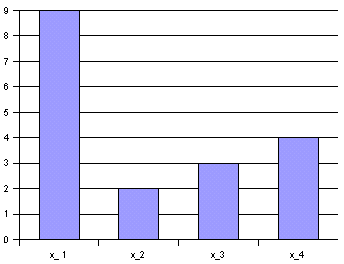
Eine Variante des Stabdiagramms ist das Balkendiagramm, bei dem die Achsen des Koordinatensystems vertauscht wurden, Stäbe also waagrecht verlaufen.

c) Die graphische Darstellung metrisch-skalierter Merkmale

Für die Darstellung metrischer Variablen werden die metrischen Qualitäten des Koordinatensystems ausgeschöpft. wobei die Häufigkeiten (absolut oder relativ) auf der Y-Achse abgetragen werden, die Variablenwerte auf der X-Achse. Bei diskreten Merkmalen wie z.B. den monetären Daten aus Tabelle 2-7 werden die Beobachtungen als Stäbe aufgetragen (vgl. nachfolgende Abb. 2-8), bei stetigen Merkmalen, wie bei der Zeit als Linie (vgl. die obige Abb. 2-5).

Abbildung 2-8: Histogramm der fiktiven Urlaubs-Ausgaben

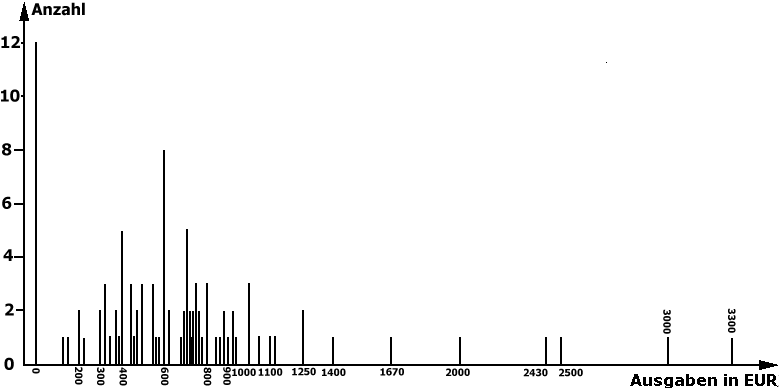
Der Vorteil und die ergänzende Funktion der graphischen Darstellung liegt darin, dass die Verteilung der Ausgaben in ihrer Struktur - besser noch als in der Tabelle - auf einen Blick sichtbar wird. Hier wird sehr deutlich, dass es zwei Gruppen gibt, die überdurchschnittlich besetzt sind, zum einen die Gruppe „0 €“ und zum andern die Gruppe „600“ €. Ebenfalls sehr schön ist das Zentrum der Verteilung zu sehen. Die Ausgaben von 300 € bis 900 € liegen relativ dicht beieinander. Alle Werte darunter und darüber fallen z.T. erheblich aus dem Rahmen.

Klassierten Werten werden als Rechtecke (vgl. ebenfalls die obige Abb. 2-5) dargestellt (zur Konstruktion von Histogrammen vgl. Modul II-4). Kumulierte (absolute, relative und prozentuale) Daten lassen sich in einer Treppenfunktion darstellen, aus denen das Summenpolygon entwickelt wird.

d) Die graphische Darstellung kumulierter (metrischer) Merkmale

Entsprechend der Auf- und Abkumulation gibt es eine aufwärts- und eine abwärts verlaufende Treppenfunktion mit den entsprechenden Summenpolygonen.

Im Folgenden beziehen wir uns auf fiktive Daten der Wartezeit von Patienten in einer Arztpraxis, die wir aufkumuliert (Wartezeit in Minute von... bis unter...) bzw. abkumuliert haben (Wartezeit... und mehr):

Tabelle 2-14: Wartezeiten in einer Arztpraxis

• Die Darstellung aufkumulierter Häufigkeiten in einer Treppenfunktion

  Ausgehen von diesen Daten werden die „bis unter“- - Merkmalswerte auf der X-Achse und die kumulierten absoluten, relativen oder prozentualen Häufigkeiten , oder auf der Y-Achse abgetragen. Für jede Klasse wird nun in deren Grenzen eine Linie in Höhe des Wertes für gezeichnet. So ergibt sich die Treppenfunktion (vgl. Abb. 2-9).

  Abbildung 2-9: Aufkumulierte Treppenfunktion für die Wartezeiten in einer Arztpraxis

  

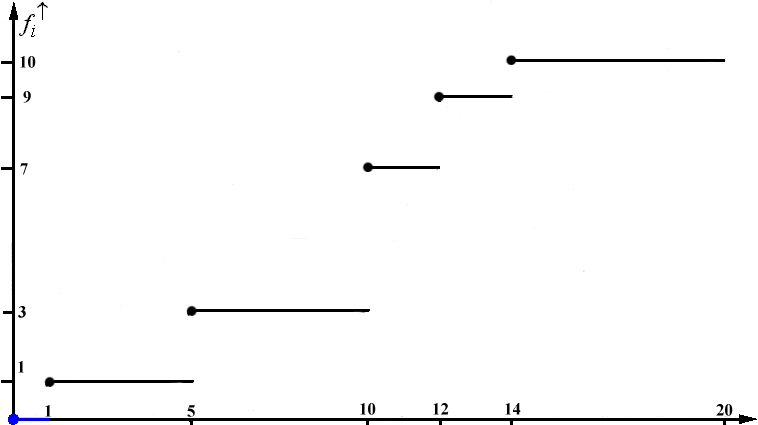
  Bei der aufkumulierte Treppenfunktion ist der Anfang der Linie durch einen Punkt gekennzeichnet. Dieser Punkt soll verdeutlichen, dass die horizontale Linie mit dem entsprechenden Abszissenwert beginnt. Der Zeichnung liegt die Annahme zugrunde, dass die in der Klasse zu verzeichnenden Häufigkeiten bereits zum herausgehobenen Merkmalswert anfallen können.

• Die Darstellung aufkumulierter Häufigkeiten in einem Summenpolygon

  Durch die Summenpolygone können die „und-mehr“- und die „weniger-als“-Methode der Kumulation in geglätteter Form visualisiert werden. Das aufkumulierte Summenpolygon verbindet die rechte Kanten der entsprechenden Treppenfunktion. Der Konstruktion dieser Kurve liegt die Hypothese zugrunde, dass die Merkmalswerte gleichmäßig über die Klassen verteilt sind (vgl. Abbildung 2-10).

  Abbildung 2-10: Aufkumuliertes Summenpolygon für die Wartezeiten in einer Arztpraxis

  

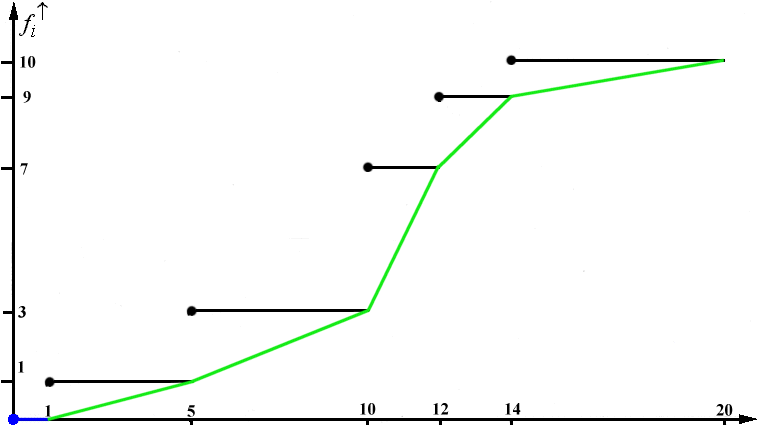
• Die Darstellung auf- und der abkumulierter Häufigkeiten in Treppenfunktionen und Summenpolygonen

  In der folgenden Grafik sind sowohl die auf- wie die absteigende Treppenfunktion und die entsprechenden Summenpolygone eingezeichnet. Treppenfunktion und Summenpolygon für die abkumulierten Werte ergeben sich aus den Spalten 5 und 6 von Tab. 2-14.

  Abbildung 2-11: Auf- und abkumulierte Treppenfunktionen und Summenpolygonen

  

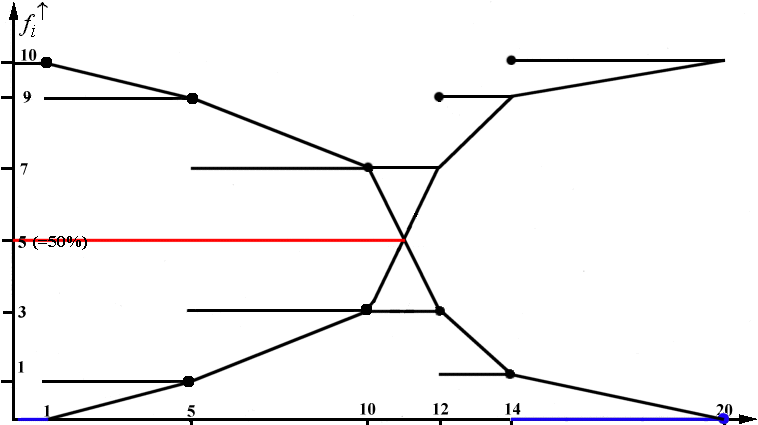
  Bei der abkumulierten Treppen-Funktion befindet sich der Kennzeichnungspunkt am Ende jeder Linie.
  Das abkumuliert Summenpolygon verbindet die entsprechenden Kennzeichnungspunkte der Treppenfunktion.

  Die beiden Summenpolygone sind um die 50%-Gerade symmetrisch. Zieht man den Schnittpunkt der beiden Summenpolygone auf die Y-Achse, so trifft dieser den N/2-Wert, hier rot dargestellt.

  Der blaue Strich soll deutlich machen, dass bei der absteigenden Treppenfunktion die letzte Klasse die Häufigkeit 0 aufweist. Dieser Sachverhalt leuchtet unmittelbar ein, wenn man sich die Bedeutung des Summenpolygons vor Augen hält. Hinter den abkumulierten Häufigkeiten steht die „und-mehr“-Methode. So gilt hier die Aussage, dass 0 Befragte 20 Minuten und mehr auf ihre Behandlung warten.

  ---

   

  letzte Änderung am 28.2.2020 um 7:49 Uhr.

  Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
  http://viles.uni-oldenburg.de/navtest/viles1/kapitel02_Tabellarische~~lund~~lgraphische~~lAufbereitung~~lstatistischer~~lDaten/modul03_Die~~lKumulation~~lstatis
  tischer~~lDaten/ebene01_Konzepte~~lund~~lDefinitionen/02__03__01__01.php3