Beispiele und Aufgaben im Modul II-2 Die tabellarische Darstellung eindimensionaler Häufigkeitstabellen
1.Beispiele
Im Folgenden behandeln wir das Problem der Datenaufbereitung am Beispiel metrischer Daten. Als Beispiel wählen wir eine fiktive Untersuchung. Dabei wurden die
jährlichen Urlaubsausgaben von N=100 Studenten an der Universität Oldenburg
ermittelt.
a) Die Urliste
Die in der Reihenfolge der Dateneingabe erstellte Urliste sieht wie folgt aus:
Tabelle 2-5: Urliste der fiktiven Urlaubsausgaben Oldenburger Studierender in EUR

Dieses Beispiel verdeutlicht sehr anschaulich den großen Nachteil einer
Urliste: Ihre Unübersichtlichkeit!
Aus diesem Grund soll nun versucht werden, die
Daten in einem ersten Schritt zu ordnen.
b) Die Primärtabelle
Wir erhalten folgende
Primärtabelle:
Tabelle 2-6: Geordnete Primärtabelle der Urlaubsausgaben in
EUR
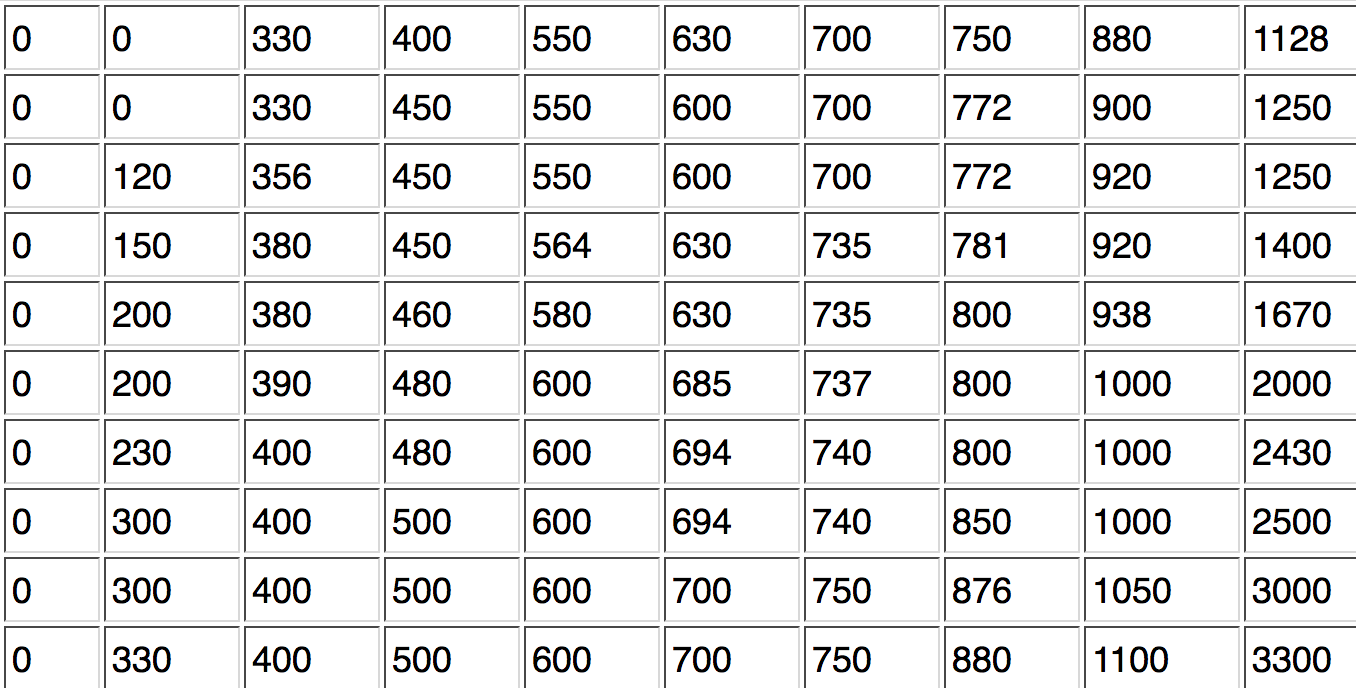
Bei der geordneten Einkommenstabelle sieht man, dass die Fälle 1 bis 12 kein Geld für Urlaub ausgegeben haben. Diese werden bei der Gruppierung in die Gruppe "0 €"
übernommen. Das gleiche geschieht mit den anderen €-Nennungen, die mehr als
einmal vorkommen.
c) Die einfache Häufigkeitstabelle
Nach der Gruppierung sollten die Daten wie folgt aussehen:
Tabelle 2-7: Gruppierte Häufigkeitstabelle der Urlaubsausgaben in €
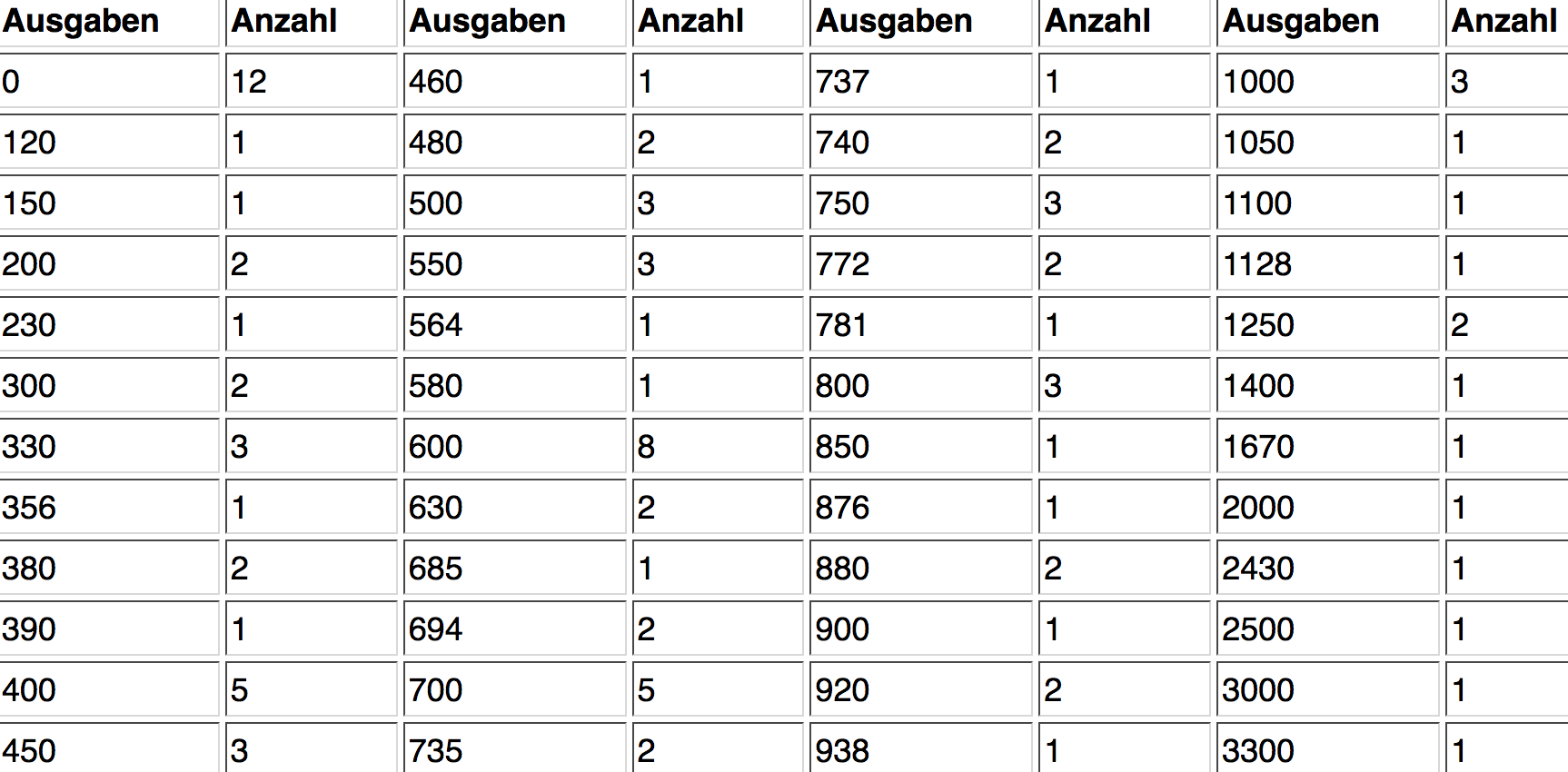
Die 100 Daten aus der Urliste wurden in 48 Gruppen zusammen gefasst. Die
Daten erlangen so eine etwas größere Übersichtlichkeit. Zu erkennen sind die Merkmalsausprägungen, die häufiger auftreten (z.B. "0", "600") und die Spannweite der Merkmalsausprägungen (0 - 3300 EUR).
Allerdings ist die Anzahl unterschiedlicher Merkmalsausprägungen noch zu groß, um sie als Tabelle präsentieren zu können. Deshalb müssen die Merkmalsausprägungen weiter zusammengefasst, d.h. klassiert werden (vgl. dazu Modul II-4). Die Klassierung führt aber zu einem Informationsverlust, da die konkreten Ausprägungen innerhalb einer Klasse verdeckt werden.
Eine Möglichkeit die Ursprungsverteilung ohne Informationsverlust zu veranschaulichen, bietet ihre graphische Darstellung in Form eines Histogramms (vgl. dazu Modul II-3).
d) Die Tabelle der auf- bzw. abkumulierten Häufigkeiten
Beim Aufkumulieren werden die Häufigkeiten beginnend mit der ersten Zeile zeilenweise addiert. Dies sei mit der folgenden Animation nochmals veranschaulicht:
Demonstration der Rechenschritte mit einfachen Daten

In einem weiteren Beispiel sollen neben den rechnerischen auch die analytischen Aspekte demonstriert werden. Gegeben sei dazu folgende klassierte Tabelle einer
fiktiven prozentualen Einkommensverteilung in €:
Tabelle 2-8: Fiktive prozentuale
Einkommensverteilung
|
Einkommen
von... bis unter... |
prozentuale Häufigkeit
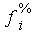 |
|
0-1000 |
13 |
|
1000-1500 |
19 |
|
1500-2000 |
25 |
|
2000-3000 |
37 |
|
3000-5000 |
6 |
|
Summe: |
100 |
Beim Aufkumulieren werden die Häufigkeiten zeilenweise addiert. D.h. für die
erste Klasse ergibt sich eine aufkumulierte Häufigkeit von 13%, in der Klasse
"bis unter 2000 €" finden sich 32% der Einkommensbezieher (13 + 19), so dass in
der Klasse "bis unter 5000 €" die Gesamtzahl der Befragten - hier N=100 % -
erscheint. Aus der oben gegebenen Tabelle resultiert also folgende Tabelle der
aufkumulierten prozentualen Einkommen:
Tabelle 2-9: Aufkumulierte prozentuale
Einkommen
|
Einkommen
bis unter ... € |
Aufkumulierte
prozentuale Häufigkeiten
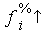
|
|
1000 |
13 |
|
1500 |
32 |
|
2000 |
57 |
|
3000 |
94 |
|
5000 |
100 |
|
- |
- |
Welche Aussagen lassen sich aus dieser Tabelle gewinnen? Mit der sog.
"bis-unter"-Methode können erste Aussagen über nicht erreichte Einkommenshöhen
gemacht werden. Wird z.B. die dritte Klasse betrachtet, lässt sich sagen, dass
57% der Leute bis unter (nicht einmal) 2000 € verdienen. Analog dazu beziehen 94% ein
Einkommen bis unter 5000 €.
Beim Abkumulieren werden die Häufigkeiten beginnend mit der ersten Zeile zeilenweise von der Gesamtzahl der Beobachtungen abgezogen. Die entsprechende Tabelle der abkumulierten prozentualen
Häufigkeiten sieht danach wie folgt aus:
Tabelle 2-10: Abkumulierte prozentuale Häufigkeiten
|
Einkommen
... und mehr € |
Abkumulierte prozentuale
Häufigkeiten
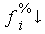
|
|
1000 |
87 |
|
1500 |
68 |
|
2000 |
43 |
|
3000 |
6 |
|
5000 |
0 |
Welche Aussage erlaubt diese Tabelle? Bei der Abkumulation werden die
überschrittenen Einkommensgrenzen ausgewiesen "mindestens ... € oder mehr". Die Tabelle informiert dann darüber,
dass 43% der Personen mindestens 2000 € und 6% mindestens 3000 € verdienen.
Vergleicht man die Ergebnisse der beiden Kumulationen, so sieht man, dass
sich die Werte in den Ergebnisspalten zu 100% aufaddieren. Die beiden
Kumulationen dienen somit auch der gegenseitigen Kontrolle der Rechnung.
e) Die Erstellung eindimensionaler Häufigkeitstabellen mit SPSS
Im folgenden Screenshot wird am Beispiel der Datei Partizipation.sav eine Tabelle der absoluten, prozentualen und aufkumulierten prozentualen Häufigkeiten mit SPSS erzeugt.
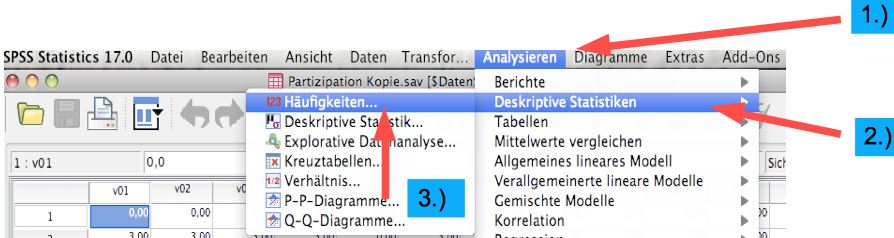
Screenshot 2-18: Erstellung einer Häufigkeitstabelle mit SPSS für das Merkmal "Status"
1.)
"Analysieren" in Funktionsleiste aufrufen.
2.) "Deskriptive Statistik" markieren.
3.) "Häufigkeiten" wählen.
Der nächste Screenshot zeigt, wie die darzustellende Variable bestimmt wird:
Screenshot 2-19: Spezifizierung des Merkmals "Status"
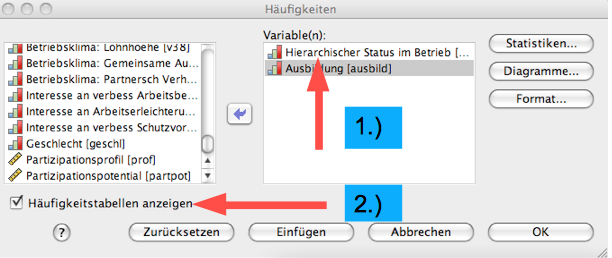
1.) Aus der Variablenliste links die gesuchte Variable markieren und mit dem Pfeil rechts neben der Liste aufrufen. Dabei können ganze Variablenblöcke ausgewählt werden.
2.) Bei sehr umfangreichen Häufigkeitsverteilungen kann das Häkchen entfernt werden, um etwa nur eine Grafik oder Statistiken anzufordern.
Mit diesen Prozeduren erhalten Sie folgendes Ergebnis:
Tabelle 2-11: Häufigkeitsverteilung des Merkmals "Status"
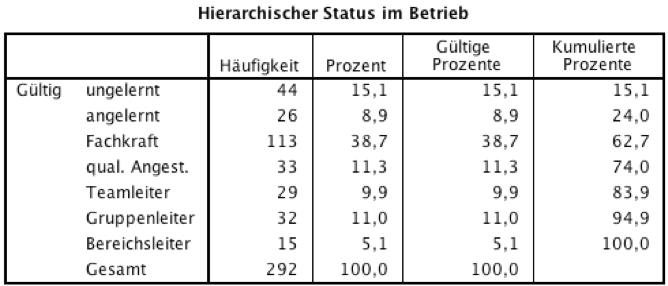
Die kumulierten prozentualen Häufigkeiten zeigen, dass 74% der Befragten keine Leitungspositionen einnehmen.
2. Aufgaben
a) Berechnung relativer und prozentualer Häufigkeiten per Hand
Da die Ordnung und Gruppierung von Daten, die sich als Datei auf eine Rechner befinden, i.A. von Programmen erledigt werden, sei hier auf eine entsprechende Aufgabe verzichtet. Auch die folgende Aufgabe zur Bestimmung von relativen und %.ualen Häufigkeiten ist eher trivial und kann auch übersprungen werden.
Als Rechenbeispiel zur tabellarischen und graphischen Aufbereitung von
statistischen Daten beziehen wir uns auf folgende Vorgaben. In einem Unternehmen
mit N=92 Beschäftigten wurde die Anzahl der Kinder pro Mitarbeiter
ermittelt.
Tabelle 2-12: Beschäftigte nach Kinderzahl
-
|
Anzahl der Kinder Xi |
absolute
Häufigkeit
fi |
|
0 |
10 |
|
1 |
22 |
|
2 |
25 |
|
3 |
18 |
|
4 |
11 |
|
5 |
6 |
Berechnen Sie daraus die relativen und prozentualen Häufigkeiten.
Kommentieren Sie Ihre Ergebnisse.
Eine Musterlösung finden Sie nachfolgend:
Tabelle 2-13: Absolute, relative und prozentuale Häufigkeiten der
Kinderzahl
-
|
Anzahl der Kinder |
absolute
Häufigkeit
fi |
relative
Häufigkeit
fi' |
prozentuale
Häufigkeit
fi% |
|
0 |
10 |
0,1087 |
10,8696 % |
|
1 |
22 |
0,2391 |
23,9130 % |
|
2 |
25 |
0,2717 |
27,1739 % |
|
3 |
18 |
0,1957 |
19,5652 % |
|
4 |
11 |
0,1196 |
11,9565 % |
|
5 |
6 |
0,0652 |
6,5217 % |
|
Summe: (Werte gerundet) |
92 |
1 |
100 % |
Wie ersichtlich, sind die prozentualen Angaben wesentlich
griffiger als die absoluten und die relativen.
b) Interaktive Aufgabe zur Berechnung kumulierter Häufigkeiten
Im Folgenden finden Sie zwei Aufgaben anhand derer Sie die Rechenschritte der Auf- und Ab-Kumulation noch einmal einüben können.
Sie können dabei die Berechnungen mehrfach mit jeweils anderen Werten wiederholen!
 (Aufkumulieren) (Aufkumulieren)
 (Abkumulieren) (Abkumulieren)
c) Aufgabe zur Erstellung von Häufigkeitsverteilungen mit SPSS
Ermitteln Sie für den Datensatz Partizipation.sav die für die folgenden Variablen:
Geschlecht,
Ausbildung,
Partizipationsprofil und
Partizipationspotential.
Interpretieren Sie Ihre Ergebnisse und vergleichen Sie die beiden zuletzt ermittelten Verteilungen!
letzte Änderung am 28.2.2020 um 7:49 Uhr.
Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles1/kapitel02_Tabellarische~~lund~~lgraphische~~lAufbereitung~~lstatistischer~~lDaten/modul02_Die~~lKlassierung~~lstati
stischer~~lDaten/ebene02_Beispiele~~lund~~lAufgaben/02__02__02__01.php3
| 




