| Druckversion: | Nach dem Drucken: | und zurück zum Dokument |
Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken
| ViLeS 1 > II Tabellarische und graphische Aufbereitung statistischer Daten |
II Tabellarische und graphische Aufbereitung statistischer Daten
- Einleitung und Modulübersicht -
1. Vorbemerkungen
Dem Einstieg in die eigentliche statistische Analyse sollen mit der Frage: "Was ist eigentlich Statistik?" einige Vorüberlegungen zu den Eigenschaften und Funktionen der Statistik (zum "Wesen" der Statistik) voran angestellt werden:
a) Was ist eigentlich Statistik?
Wenn man üblicherweise von Statistiken bzw. einer Statistik spricht, meint man entweder eine statistische Tabelle oder Graphik oder eine Maßzahl, wie z.B. einen statistischen Durchschnitt. Eine Statistik ist demnach das Ergebnis einer statistischen Berechnung.
Andererseits bedeutet ViLeS "virtuelle Lernplattform Statistik" und damit sind die Methoden angesprochen, mit denen Sie sich z.B. in einer Lehrveranstaltung "Statistik 1" befassen. Statistik ist in diesem Sinn eine Ansammlung von Methoden.
Für ein angemessenes Verständnis der statistischen Analyse und ihrer Ergebnisse sind beide Sinngehalte bedeutsam, weil sie unmittelbar aufeinander bezogen sind. Jedes statistische Ergebnis resultiert aus einer spezifischen Methode und der Art und Weise, wie sie eingesetzt wurde, und ist auch nur vor dem Hintergrund dieser Methode zu verstehen und korrekt zu interpretieren.
b) Statistik als Methode und als quantitatives Modell der Realität
Als Methode gibt die Statistik vor, mit welchen tabellarischen, graphischen oder rechnerischen Verfahren bestimmte Typen von Daten (nach ihrem Skalenniveau) zu behandeln sind.
Als Modell charakterisiert die Statistik einen spezifischen Ausschnitt der Realität (vgl. dazu auch die verschiedenen Modelle der Realität im Schaubild zum empirisch-statistischen Informations- und Forschungsprozesses in Abb. 1-2 im Kap. I). Was bedeutet nun aber Modell der Realität ?
Das kann man sich einfach an einem Strömungsmodell eine PKWs oder an einem Dummy in einem Crashtest klar machen: Beide Modell wurden konstruiert um die Realität zu erfassen, allerdings nicht in ihrer Komplexität sondern nur in einem Ausschnitt, da aber möglichst exakt, um ein konkretes Problem realitätsnah lösen zu können (vgl. dazu Abb. 2-1).Abbildung 2-1: Statistik als quantitatives Modell der Realität
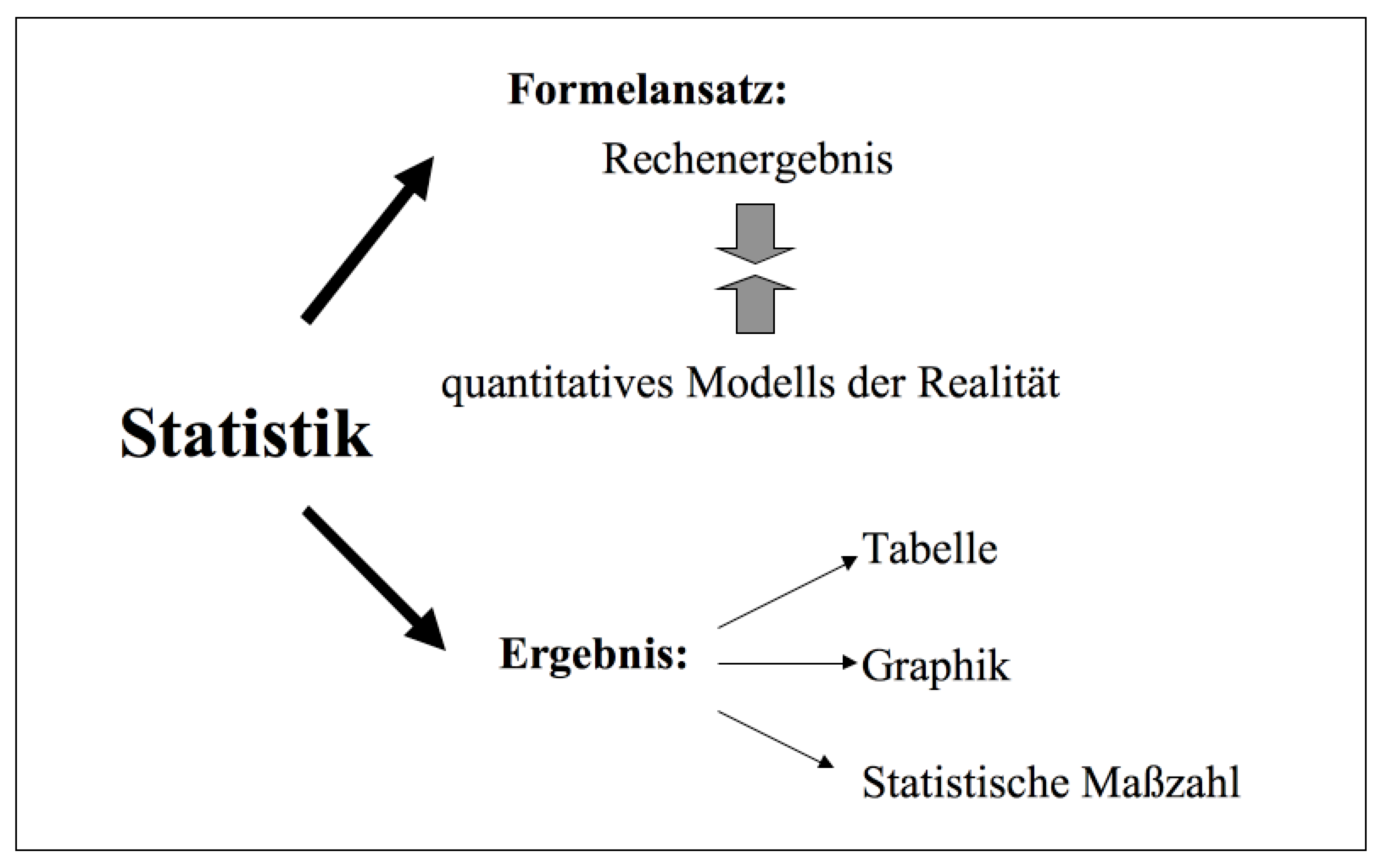
c) Die Bevölkerungspyramide als Modell der Bevölkerungsstruktur
Stellen wir uns vor ein Gemeinderat möchte sich einen realistischen Blick der Bewohner-/innen der Gemeinde verschaffen. Dazu bitte der Bürgermeister alle Gemeindemitglieder auf den Sportplatz und ordnet an, dass die weiblichen Personen sich links der Mittellinie und die männlichen sich rechts aufstellen sollen und zwar die Säuglinge in ihren Kinderwagen in der 1. Reihe, danach in der 2. Reihe die Einjährigen in ihren Buggies, in der 3. Reihe die Zweijährigen in ihren Bobbiecars usw. bis in den letzten Reihen die Älteren in ihren Rollatoren stehen. Als statistische Graphik wäre dieses reale Bild als Bevölkerungspyramide zu zeichnen. Diese Begriff der Pyramide stammt aus der Frühzeit der Statistik und ist höchsten noch zu Beginn des vorangegangenen Jahrhunderts zutreffend (vgl. Abb. 2_2)
Abbildung 2-2: Bevölkerungspyramide 1910
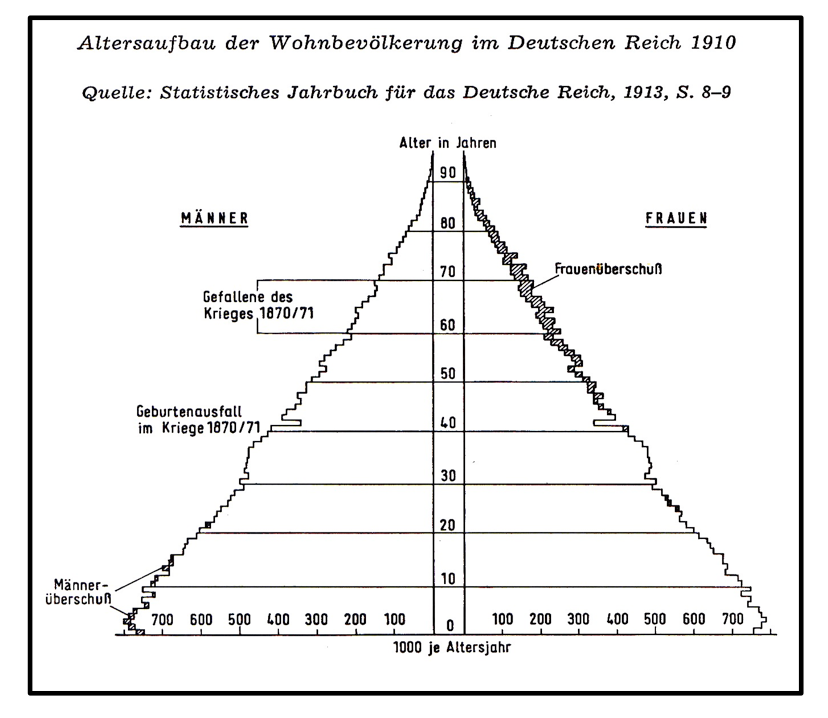
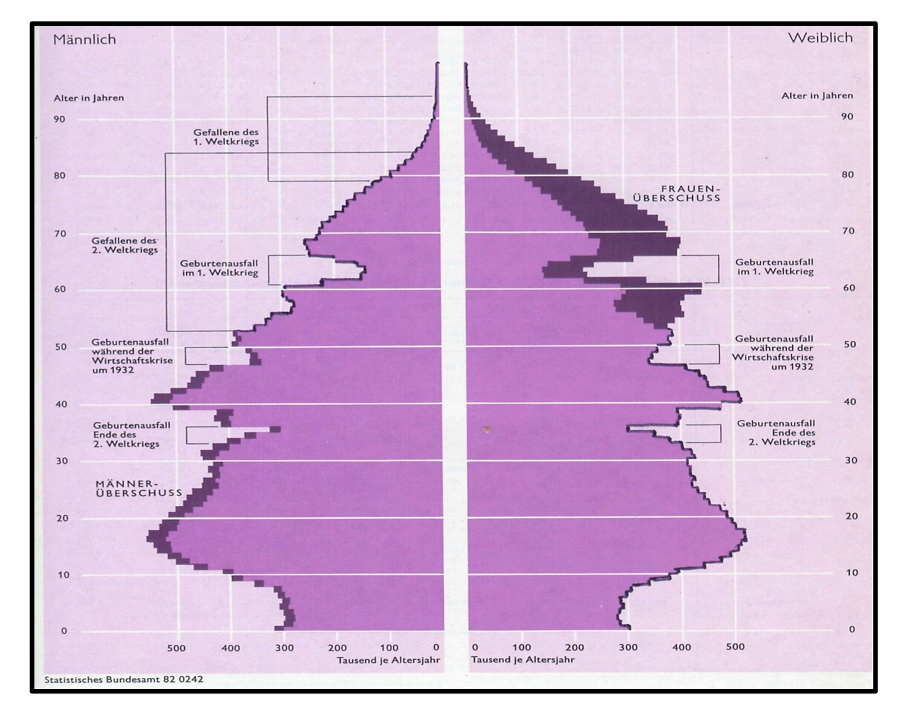
Vergleicht man die Darstellung für das Jahr 1910 mit der für das Jahr 1980, so zeigen sich anhand der textlichen Verweise plastisch sowohl die demographischen Umbrüche (konstante jährliche Sterblichkeitsquoten in 1910 und veränderte Geburtenquoten ab 1965) wie die gesellschaftlichen Katastrophen des 20. Jahrhunderts (in Form von Wirtschaftskrisen und Weltkriegen).
Abbildung 2-3: Bevölkerungspyramide 1980
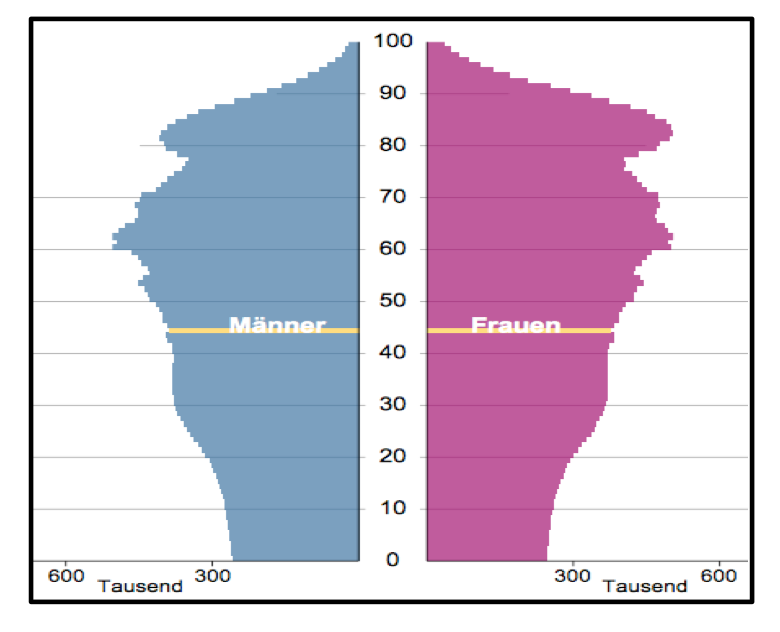
Weitere 70 Jahre später, diesmal als Prognose, wird der demographische Wandel vollends deutlich, so dass der Begriff der "Pyramide" endgültig überholt ist.
Abbildung 2-4: Bevölkerungspyramide 2050
Ein interaktives applet des Statistischen Bundesamtes zur Bevölkerungsentwicklung 1950 - 2060 finden Sie unter diesem externen Link .
Die gezeigten Graphiken verdeutlichen sowohl den Modellcharakter der statistischen Graphik wie deren Fähigkeit, auch komplexe Sachverhalte "auf einen Blick" zu erschließen.
2. Modulüberblick
a) Die Datengrundlage
Bei der Aufbereitung statistischer Daten sollen die aus einer Befragung einzelner Personen, Institutionen (Unternehmen) oder sonstiger Merkmalsträger resultierenden Informationen systematisch zusammengestellt und mit einfachen Methoden ausgewertet werden. Dazu betrachten wir im folgenden Kapitel die jeweiligen Merkmale separat.
In den Erhebungsunterlagen wird jede individuelle Ausprägung eines Merkmals einzeln erfasst. Deshalb müssen in einem ersten Schritt diese Angaben für jedes Merkmal gesammelt werden. So entsteht für jedes Merkmal eine Urliste (auch Strichliste oder Primärtabelle genannt). Es sind in ihr noch keine Zusammenfassungen von Objekten gleicher Merkmalsausprägungen in Gruppen oder Klassen vorhanden.
Für die späteren Analysen wird ein Datensatz vorgestellt, der mit dem Datenanalyseprogramm SPSS ausgewertet werden soll. Dieses wird in einem Exkurs kurz skizziert. Dabei werden einige zentrale Funktionen des Programms erläutert, die Generierung eines Datensatzes beschrieben, der Import von Excel-Dateien erklärt und erste Analyseschritte präsentiert.
b) Die tabellarische Darstellung der eindimensionalen Häufigkeitsverteilung
Mit der Weiterverarbeitung der Daten in der Datendatei wird eine leichtere Aufnahme und Verdichtung der Information angestrebt. Dazu wird eine Ordnung und Gruppierung dieser Daten durchgeführt. Durch die Gruppierung wird ermittelt, wie häufig die einzelnen Merkmalsausprägungen auftreten. Deshalb wird die Anzahl der Beobachtungen einer bestimmten Merkmalsausprägung in der Statistik als Häufigkeit bezeichnet und die gruppierte Verteilung der Merkmale als einfache Häufigkeitsverteilung. Diese kann in Form einer Tabelle oder in Form einer Graphik dargestellt werden. Beide Präsentationsformen werden im Detail und auch für die folgenden Aufbereitungsweisen statistischer Informationen vorgestellt.
In den meisten Fällen liegen die statistischen Daten in absoluten Häufigkeiten (engl. frequencies) vor. Absolute Häufigkeiten werden unmittelbar als Information benutzt. Relative und prozentuale Werte erlauben einen besseren Vergleich mehrerer Verteilungen, in denen die Anzahl der betrachteten Objekte nicht gleich ist.
Eine weitere wichtige Form der Aufbereitung gruppierter Daten stellt die sog. Kumulation dar. Das Auf- und Abkumulieren (auch Kumulieren und Dissipieren) von Werten erfüllt in der Statistik mehrere Funktionen. So wird es z.B. genutzt, um Teilmengen von Beobachtungen zu beschreiben. Mit einer Zusammenfassung von Merkmalsausprägungen "bis unter ..." und "mehr als ..." können z.B. Aussagen über die Häufigkeit der Familien mit weniger als drei Kindern oder einem Einkommen von mehr als 4800 DM gemacht werden.
Im Arbeitsschritt "Beispiele und Aufgaben" des Moduls werden dazu die Möglichkeiten vorgestellt, tabellarische Auswertungen von Datensätzen mit SPSS durchzuführen.c) Die graphische Darstellung der eindimensionalen Häufigkeitsverteilung
Unmittelbar anschaulich können diese Häufigkeitsverteilungen auch grafisch dargestellt werden. Dazu stehen mehrere graphische Formen, wie Kreis-, Stab- und Liniendiagramme zur Verfügung. Die optimale Darstellungsform hängt dabei insbesondere vom Skalenniveau ab.
Die graphische Darstellung auf- bzw. abkumulierte Daten erfolgt über die Treppenfunktion und das Summenpolygon.
Im Arbeitsschritt "Beispiele und Aufgaben" des Moduls werden dazu die Möglichkeiten vorgestellt, graphische Darstellung eindimensionaler Häufigkeitsverteilungen mit SPSS zu erzeugen.d) Die tabellarische Darstellung der klassierter Häufigkeitsverteilung
Da gruppierte Daten meist zu unübersichtlich sind, werden sie in der Regel weiter zusammengefasst. Dies führt zur sog. klassierten Häufigkeitsverteilung. Dazu sind für die einzelnen Merkmalsausprägung Klassen zu bilden. Die relevanten Informationen bestehen aus der Klassenuntergrenze, der Klassenobergrenze, der Klassenbreie und der Häufigkeit, der in dieser Klasse befindlichen Beobachtungen.
e) Die graphische Darstellung der klassierten Häufigkeitsverteilung
Bei Klassierungen mit ungleichen Klassenbreiten ist nicht mehr ausschließlich die absolute Häufigkeit interessant, sondern ebenso die sog. Häufigkeitsdichte. Diese findet vor allem Eingang in die graphische Präsentation klassierter Daten im Histogramm.
f) Die eigenständige statistische Analyse mit SPSS
In diesem Modul sollen die Möglichkeiten eigenständiger statistischer Analysen mit den SPSS-Beispielsdaten aus dem Mikrozensus oder mit unter Verwendung des Fragebogengenerators selbst erhobenen Daten vorgestellte werden.
3. Modulwahl
Wählen Sie ein Modul:
- II-1 Die Datengrundlage
- II-2 Die tabellarische Darstellung eindimensionaler Häufigkeitsverteilungen
- II-3 Die graphische Darstellung eindimensionaler Häufigkeitsverteilungen
- II-4 Die tabellarische Darstellung klassierter Daten
- II-5 Die graphische Darstellung klassierter Daten
- II-6 Eigene Analysen mit Mikrozensus-Daten