Grundlagen der deskriptiven Statistik mit Microsoft Excel
Inhalt:
I. Datenaufbereitung
II. Eindimensionale Häufigkeitsverteilungen
1. Gruppierung
2. Klassierung
3. Maßzahlen
III. Zweidimensionale Häufigkeitsverteilungen
1. Darstellung
2. Kontingenzanalyse
3. Rangkorrelation
4. Regression und Korrelation
I. Datenaufbereitung
Die statistische Datenanalyse mit
Excel erfordert eine Aufbereitung des zu untersuchenden
Zahlenmaterials. Dieses ist zunächst zeilen- und spaltenweise
einzugeben, wobei zu berücksichtigen ist, dass die Nummerierung
auf der vertikalen Leiste des Tabellenfensters Merkmalsträger
(Personen, Objekte, Zeitpunkte) betrifft und die Buchstaben auf der
horizontalen Leiste deren Charakteristika als spaltenweise notierte
Variablen bezeichnen.
Es wird im Folgenden stets davon ausgegangen, dass
Merkmalsausprägungen innerhalb der Datenmatrix nur in Form
numerischer Codierungen erscheinen.
Die Eingabe erfolgt entweder direkt über die Tastatur oder
mittelbar durch eine Eingabemaske. Im Falle der direkten Eingabe
empfiehlt es sich, die zeilenweise Notation mit Hilfe des
Nummerblocks der Tastatur und der Tabulatortaste
 durchzuführen. Falls nicht zu viele Variablen einzugeben sind,
kann eine Eingabemaske verwandt werden. Hierfür sind
Überschriften für jede Variable erforderlich. Man setzt den
Cursor in die äußerst linke Spalte der Überschriftenzeile.
Über Daten -> Maske lassen sich
die Werte zeilenweise in das Tabellenblatt einfügen.
durchzuführen. Falls nicht zu viele Variablen einzugeben sind,
kann eine Eingabemaske verwandt werden. Hierfür sind
Überschriften für jede Variable erforderlich. Man setzt den
Cursor in die äußerst linke Spalte der Überschriftenzeile.
Über Daten -> Maske lassen sich
die Werte zeilenweise in das Tabellenblatt einfügen.
Sollten die Daten der Tabelle eines anderen Programms entspringen
(z.B. SPSS), können sie kopiert werden. Im Falle einer
SPSS-Datenmatrix geschieht dies auf üblichem Wege durch
Markierung aller Zellen -> rechte
Maustaste -> Kopieren -> Cursor in die Excel-Datei ->
rechte Maustaste -> Einfügen.
Im Excel-Dokument ist es nötig, die Spaltenüberschriften in
das Tabellenblatt einzubringen, während die oberste Zeile stets
mit Buchstaben besetzt bleibt.
Für die Analyse ist die Übersichtlichkeit von Bedeutung. So
sollten die Variablenüberschriften einen Abstand mehrerer Zeilen
vom obersten Rand aufweisen. Dies erscheint notwendig, um
statistische Maßzahlen zur Charakterisierung einzelner
Variablen zuordenbar notieren zu können. Darüber hinaus
sollten die Überschriften vom Zahlenmaterial wenigstens eine
Zeile Abstand aufweisen. Über das Modul Einfügen -> Zeilen lassen sich solche Abstände erzeugen. Zur
erhöhten Übersicht ist es ferner relevant, die Höhe
bzw. Breite von Zeilen und Spalten zu minimieren. Hierzu ist das
gesamte Tabellenblatt durch Anklicken des obersten linken Punktes
(neben A, über 1) zu markieren. Durch Format -> Zeile -> Optimale Höhe
und Format -> Spalte -> Optimale Breite werden die Zellflächen auf das
Mindeste reduziert. Schließlich können die
Spaltenüberschriften verengt werden, indem man die Überschriften
markiert und über die rechte Maustaste „Zellen
formatieren“ anklickt. Durch eine Vertikalisierung der
Überschrift, ein Zeilenumbruch oder die Funktion „An
Zellgröße anpassen“ können die Spalten noch
enger konfiguriert werden, so dass man im günstigsten Fall alle
Variablenspalten übersehen kann.
Excel bietet die Möglichkeit, Variablen auf- oder absteigend zu
sortieren. Dies kann bei der Datenaufbereitung von Nutzen sein, wenn
eine spezifische ordinale oder metrische Variable untersucht wird.
Man wählt die Funktion Daten ->
Sortieren, in der die Ordnungsrichtung (aufsteigen/absteigend) sowie
der zu sortierende Spaltenbereich festgelegt werden. Excel passt die
anderen Merkmale der nun vertauschten Merkmalsträger
entsprechend an. Selbstverständlich kann eine Sortierung nur für
eine Variable gelten, an deren Reihenfolge sich andere Merkmalsträger
automatisch anpassen.
Von besonderer Bedeutung für eine Präparierung der Daten
ist die Filterfunktion. Mit ihrer Hilfe können fehlcodierte
Merkmalsausprägungen („missing values“), die zumeist
mit „-1“ bezeichnet werden, erkannt und entfernt werden.
Durch Daten -> Filter -> AutoFilter und das anschließende Anklicken des
Symbols
 oberhalb der Variablen werden sämtliche Ausprägungen einer
Variablen aufgelistet. Ruft man in einer Variablen die mit „-1“
codierten Objekte auf, lassen sich diese markieren und durch die
Taste
oberhalb der Variablen werden sämtliche Ausprägungen einer
Variablen aufgelistet. Ruft man in einer Variablen die mit „-1“
codierten Objekte auf, lassen sich diese markieren und durch die
Taste
 beseitigen.
beseitigen.
Für die sich anschließende
Analyse ist es bedeutsam, die Datenmatrix für größere
Outputs (z.B. Grafiken) von den Ergebnissen zu separieren. Eine
vorteilhafte Übersichtlichkeit lässt sich durch zwei
Tabellenblätter herstellen, wobei ersteres die Datenmatrix,
letzteres die Untersuchungsresultate enthält.
II. Eindimensionale Häufigkeitsverteilungen
Eindimensionale Häufigkeitsverteilungen beziehen sich auf die
Darstellung und Analyse einer Variablen. Ausgehend von einer
mehrdimensionalen Datenmatrix ist es sinnvoll, die jeweilige
Variablen für eine nähere Untersuchung in das
Analysefenster zu kopieren.
1. Gruppierung
Variablen in der Datenmatrix enthalten Einzelwerte. Um zu einer
höheren Übersichtlichkeit zu gelangen, ist es sinnvoll,
jede vorkommende Einzelausprägung nur einmalig zu nennen und ihr
die Häufigkeit ihres Erscheinens zuzuordnen.
Durch die Aktivierung des Autofilters über Daten -> Filter -> Autofilter und
das anschließende Anklicken des Symbols
 oberhalb der Variablen lassen sich die vorkommenden
Einzelausprägungen ablesen und für eine gruppierte
Darstellung separat notieren. Anschließend gibt man im über
dem Tabellenblatt stehenden Analysefenster folgenden Befehl ein.
oberhalb der Variablen lassen sich die vorkommenden
Einzelausprägungen ablesen und für eine gruppierte
Darstellung separat notieren. Anschließend gibt man im über
dem Tabellenblatt stehenden Analysefenster folgenden Befehl ein.
ZÄHLENWENN (A5:A505;B13)
A5:A505 steht hier beispielhaft für den Bereich der in
Einzelwerten notierten Variablen. B13 ist ein Beispiel für den
Standort der zu zählenden Merkmalsausprägung.
Stehen die abzuzählenden Werte untereinander, muss man lediglich
das Rechteck der markierten Zelle, in der das erste Zählergebnis
steht, mit der Maus anklicken und bis zur letzten Merkmalsausprägung
herunterziehen. Die Gruppierung ist damit komplett.
Um rasch Häufigkeitsverhältnisse im Vergleich der
Merkmalsausprägungen zu erkennen, erscheint eine Prozentuierung
nötig. Die relative Häufigkeit der ersten
Merkmalsausprägung generiert man durch Eingabe ihres Standorts
dividiert durch die Summe aller Probanden. Die Summe lässt sich
durch Markierung des zu summierenden Bereiches und Bestätigung
des Summenzeichens
 in der Menüleiste ermitteln. Bei der Division ist es bedeutsam,
im Divisor (der Summe) ein Dollarzeichen zu setzen.
in der Menüleiste ermitteln. Bei der Division ist es bedeutsam,
im Divisor (der Summe) ein Dollarzeichen zu setzen.
Beispiel:
C5 / C$10 = 0,1516
| |
74 Summe von 488
Auf diesem Wege wird die Summe (der Divisor) fixiert.
Jetzt muss das Ergebnisfeld wie beim Auszählen nur noch nach
unten gezogen werden, um die restlichen Merkmalsausprägungen zu
relativieren.
Um endlich Prozentwerte zu erhalten, markiert man den Bereich
relativer Zahlen, klickt ihn mit der rechten Maustaste an und wählt
„Zellen formatieren“. Durch Zahlen -> Prozent erhält man die endgültige Prozentuierung.
Für eine grafische Darstellung gruppierter Daten jeden
Skalenniveaus eignen sich Balken- und Kreisdiagramme. Ausgehend von
den gruppierten Merkmalsausprägungen und ihren absoluten
Häufigkeiten sind erstere zu markieren und über die rechte
Maustaste -> Zellen formatieren -> Text als spätere Beschriftungen vorzubereiten.
Anschließend markiert man die Spalten für
Merkmalsausprägungen und die absolute Häufigkeiten. Endlich
wählt man über Diagramm ->
Diagrammtyp eine geeignete Darstellungsform.
2. Klassierung
Im Falle metrischer Daten lassen sich die Merkmalsausprägungen
unter Inkaufnahme eines Informationsverlustes weiter verdichten. Dies
geschieht durch Bildung von Klassen. Hierzu sind obere Klassengrenzen
in eine separate Spalte einzutragen. Im Gegensatz zur üblichen
Definition von Klassengrenzen interpretiert Excel die eingegebenen
Klassengrenzen im Sinne eines Intervalls „... bis
einschließlich“.
Man wählt Extras ->
Analyse-Funktionen -> Histogramm. Im
Eingabebereich des erscheinenden Fensters ist der zu klassierende
Bereich einzutragen. In den Klassenbereich gehören die
Standortbezeichnungen der oberen Klassengrenzen.
Im selben Fenster lässt sich eine „Diagrammdarstellung“
anklicken. Das Ergebnis ist jedoch nur ein Balkendiagramm. Um ein
Histogramm im Sinne einer flächenproportionalen Zuordnung zu
erhalten, werden gleiche Klassenbreiten vorausgesetzt. Ferner sind
durch Doppelklick auf die Balken ->
Optionen -> Abstand = 0 die Abstände
der Balken zu beseitigen.
Um die Tabelle klassierter Daten zu einer für die weitere
Analyse anwendbaren Arbeitstabelle zu erweitern, sollten Spalten
hinzugefügt werden. Zunächst erscheint die Klassenbreite
von Bedeutung, die sich als Differenz der Zellenbezeichnung der
oberen und unteren Klassengrenzen ergibt. Daneben ist die
Klassenmitte als arithmetisches Mittel der oberen und unteren
Klassengrenze einzugeben. Weiters lässt sich die
Häufigkeitsdichte als Quotient aus absoluter Häufigkeit und
Klassenbreite vermerken. Abschließend sind Auf- und
Abkumulationen von Bedeutung. Erstere ergeben sich als Summen der
absoluten Häufigkeit einer Merkmalsausprägung und der ihr
vorhergehenden Summen. Die Abkumulation resultiert aus der Differenz
der summierten Häufigkeit und der jeweiligen Klassenhäufigkeit.
Von Bedeutung ist die einmalige Eingabe der Formeln. Excel kopiert
die jeweilige Gleichung und wendet sie äquivalent auf die
anderen Spaltenelemente an.
3. Maßzahlen
Eindimensionale Häufigkeitsverteilungen können durch
Maßzahlen untersucht werden.
Aufschlussreich sind Mittelwerte. So gibt der Modus die häufigste
Merkmalsausprägung an. Er wird ermittelt über Eingabe der
Formel MODALWERT(A5:A505) im Analysefenster. „A5:A505“
steht exemplarisch für den Standort der zu untersuchenden
Verteilung. Der Median als Zentralwert einer Verteilung, der diese in
gleich große Hälften spaltet, ergibt sich äquivalent
durch die Eingabe von MEDIAN(A5:A505). Schließlich kann man das
arithmetische Mittel als Durchschnitt aller Merkmalsausprägung
durch MITTELWERT(A5:A505) erzeugen.
Um Mittelwerte in ihrer Aussagefähigkeit zu beurteilen, zieht
man Streuungsmaße heran.
Die Spannweite ergibt sich als Differenz aus höchster und
niedrigster Merkmalsausprägung, wobei das Maximum über die
Formel MAX(A5:A505) und das Minimum durch MIN(A5:A505) erzeugt
werden.
Der Semiquartilsabstand gibt die durchschnittliche Abweichung vom
Median an. Er resultiert als halbe Differenz aus dem dritten und dem
ersten Quartilswert. Diese lassen sich ermitteln über die
Formeln QUARTILE(A5:505,1) und QUARTILE(A5:505,3), wobei A5:A505
jeweils Beispiele für die zu untersuchenden Zellenstandorte sind
und 1 bzw. 3 für das jeweilige Quartil stehen.
Für eine Bewertung des arithmetischen Mittels dienen die
mittlere absolute Abweichung und die mittlere quadratische
Abweichung.
Die mittlere absolute Abweichung wird als Differenz jeder einzelnen
Merkmalsausprägung mit dem arithmetischen Mittel kalkuliert.
Hiefür gibt man in das Analysefenster die Differenz zwischen
Zellbezeichnung eines Variablenwertes und der Zellbezeichnung des
arithmetischen Mittels ein, wobei vor die Zahl der letzten
Bezeichnung ein Dollarzeichen zu setzen ist. So wird das
arithmetische Mittel fixiert. Durch Anklicken des Quadrates der
markierten Ergebniszelle und Herabziehen bis zum letzten Objekt
werden alle weiteren Abweichungen erzeugt. Um statt negativer
Differenzen nur positive Ergebnisse zu erhalten, sind alle
Differenzen zu markieren, ihre Formel im Analysefenster einzuklammern
und vor diese die Funktion ABS zu notieren. Schließlich ist
noch das arithmetische Mittel aus den (jetzt) positiven Differenzen
zu bilden, so dass die mittlere absolute Abweichung verbleibt.
Die mittlere quadratische Abweichung (Varianz) kann über Eingabe
der Formel VARIANZ(A5:A505) ermittelt werden. Durch
VARIANZ(A5:A505)^(1/2) resultiert die Standardabweichung als Maß
der durchschnittlichen Abweichung vom Mittelwert.
Die bis hierhin generierten einzelnen
Maßzahlen können ergänzt um weitere Maße wie
dem Pearsonschen Schiefemaß auf einmal errechnet werden. Dies
geschieht über Extras ->
Analyse-Funktionen ->
Populationskenngrößen. Nachteil dieser Gesamtdarstellung
ist die Unabhängigkeit des Outputs von den Ursprungsdaten. Bei
deren Veränderung ändert sich ein statistisches Maß
-wie sonst bei Excel üblich- nicht automatisch mit.
Excel kennt keine statistischen Konzentrationsmaße. Man kann
Maße der relativen Konzentration, nämlich den
Gini-Koeffizienten und die Lorenzkurve mit Hilfe des ETC-Programmes
auf der ViLeS-Website www.viles-stat.de
errechnen. Der präzise Weg lautet ViLeS
1 ->
Statistische
Konzentrationsmaße -> Die
relative Konzentration -> Beispiele und eigene Analysen.
III. Zweidimensionale Häufigkeitsverteilungen
1. Darstellung
Um zwei Variablen gemeinsam darzustellen, bedient man sich der
Kontingenztabelle. Sie enthält die Häufigkeiten des
bedingten und unbedingten Auftretens jeder Merkmalsausprägung.
In Excel lassen sich
Kontingenztabellen sehr leicht über Extras -> Pivot-Table herstellen. Ausgegangen wird von der
Datenmatrix, die keinen Abstand zu ihren Spaltenüberschriften
aufweist. Der Cursor wird in die Zelle der am linken Rand stehenden
Überschrift gesetzt. Anschließend ruft man das genannte
Modul auf und wählt „Fertig stellen“. Es erscheint
eine noch unbesetzte Tabelle und das Makro „Pivot-Table“,
in dem alle Variablen mit ihrer Überschrift genannt sind. Nun
kann man wahlweise zwei Variablen jeden Skalenniveaus in die
Summenspalte bzw. Summenzeile der Tabelle ziehen. Um sich bedingte
und unbedingte Häufigkeiten anzeigen zu lassen, muss eine der
Variablen nochmalig ins Innere der Tabelle gezogen werden.
Für einen besseren Umgang mit der Pivottabelle erscheint es
sinnvoll, diese nur als Werte zu kopieren und die Kopie weiter
zu analysieren. Dies geschieht über Markieren der Pivottabelle -> Bearbeiten -> Kopieren -> Cursor in ein neues Feld ->
Bearbeiten -> Inhalte einfügen
-> Werte -> OK.
Eine grafische Darstellungsform, in der die Ausprägungen einer
Variablen als Kategorien auf die Abszisse gelangen und die in diesen
Kategorien (grafisch Balken) vorkommenden Ausprägungen der
anderen Variablen anteilsmäßig dargestellt werden,
erreicht man über Markierung der bedingten Häufigkeiten
innerhalb der Tabelle ->
Diagrammassistent -> Säule -> dritte Abbildung der obersten Optionen -> Fertigstellen.
2. Kontingenzanalyse
Die Kontingenzanalyse zielt auf die Untersuchung zweier nominal
skalierter Daten ab. Das für eine solche Analyse bedeutsamste
Maß ist Chi-Quadrat. Es kann über den Funktionsassistenten
-> Statistik -> CHITEST ermittelt werden. Im erscheinenden Fenster sind als
beobachtete Werte (Beob_Meßwerte) die bedingte Häufigkeit
der Kontingenztabelle einzutragen. Als erwartete Werte (ERWART_WERTE)
sind die vorab selbst zu errechnenden Äquivalente der
Indifferenztabelle einzutragen. Es resultiert Chi-Quadrat.
Excel kennt keine expliziten Kontingenzmaße, wie Phi, Cramers
V, Pearsons C oder das Chi-Quadrat-unabhängige Lambda.
Allerdings lassen sich die einzelnen Formeln relativ leicht in das
Analysefenster übertragen.
Im Übrigen ermöglicht das ETC-Programm die Kalkulation von
Zusammenhangsmaßen durch Eingabe der Kontingenztabelle. Zum
entsprechenden Modul gelangt man über www.viles-stat.de
ViLeS
1 ->
Zweidimensionale
Häufigkeitsverteilungen und Zusammenhangsmaße für
nominalskalierte Variablen ->auf
Chi-Quadrat basierende Maßzahlen ->einfache Anwendung.
3. Rangkorrelation
Excel kennt keine Maße zur Zusammenhangsanalyse von
Ordinaldaten. Allerdings kann es die Arbeit der Rangeinteilung
erleichtern.
Man setzt den Cursor in eine Spalte neben der zu analysierenden.
Anschließend trägt man im Analysefenster
RANG(A5,A5:A505)
ein, wobei A5 den Standort der mit einem Rang zu versehenden Zahl ist
und A5:A505 der Bereich, welcher vollständig nach Rängen
sortiert werden soll. Durch Anklicken des Rechtecks der markierten
Ergebniszelle und Herunterziehen ergeben sich die restlichen
Rangeinteilungen.
Im Weiteren lässt sich beispielsweise der Spearmansche
Rangkorrelationskoeffizient ermitteln. Die entstehenden „Rangspalten“
werden voneinander abgezogen, quadriert und summiert. Das Ergebnis
lässt sich in die Formel
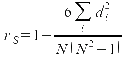 einsetzen:
einsetzen:
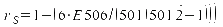 .
.
4. Regression und Korrelation
Die Zusammenhangsanalyse metrischer Variablen impliziert zwei
Erkenntnisziele, nämlich die Stärke und die Richtung eines
Zusammenhanges.
Vor einer Untersuchung der Zusammenhangsrichtung erscheint die
Erkenntnis der Stärke wichtig, weil eine schwache Korrelation
die Regression überflüssig machte. Über Extras -> Analyse-Funktionen ->
Korrelation enthält man ein Fenster, in das die Spalten der
metrischen Variablen einzugeben sind. Es resultiert der
Korrelationskoeffizient nach Bravais-Pearson.
Die Regressionsgleichung ergibt sich durch Extras -> Analyse-Funktionen ->
Regression und Eingabe der Spaltenbezeichnungen für die
metrischen Variablen.
Zur Generierung eines Streudiagramms mit Regressionsgerade markiert
man zunächst die abzubildenden Variablen in ihren Spalten und
ruft über den Diagrammassistenten „Punkt (XY)“ auf.
Im resultierenden Streudiagramm ist die Punktwolke zu markieren.
Anschließend betätigt man die rechte Maustaste und wählt
„Trendlinie hinzufügen“. Im sich öffnenden
Fenster wird die Geraden selektiert. Mit
 erscheint die Regressionsgerade im Streudiagramm.
erscheint die Regressionsgerade im Streudiagramm.
 durchzuführen. Falls nicht zu viele Variablen einzugeben sind,
kann eine Eingabemaske verwandt werden. Hierfür sind
Überschriften für jede Variable erforderlich. Man setzt den
Cursor in die äußerst linke Spalte der Überschriftenzeile.
Über Daten -> Maske lassen sich
die Werte zeilenweise in das Tabellenblatt einfügen.
durchzuführen. Falls nicht zu viele Variablen einzugeben sind,
kann eine Eingabemaske verwandt werden. Hierfür sind
Überschriften für jede Variable erforderlich. Man setzt den
Cursor in die äußerst linke Spalte der Überschriftenzeile.
Über Daten -> Maske lassen sich
die Werte zeilenweise in das Tabellenblatt einfügen.
 oberhalb der Variablen werden sämtliche Ausprägungen einer
Variablen aufgelistet. Ruft man in einer Variablen die mit „-1“
codierten Objekte auf, lassen sich diese markieren und durch die
Taste
oberhalb der Variablen werden sämtliche Ausprägungen einer
Variablen aufgelistet. Ruft man in einer Variablen die mit „-1“
codierten Objekte auf, lassen sich diese markieren und durch die
Taste
 beseitigen.
beseitigen.

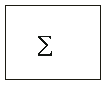 in der Menüleiste ermitteln. Bei der Division ist es bedeutsam,
im Divisor (der Summe) ein Dollarzeichen zu setzen.
in der Menüleiste ermitteln. Bei der Division ist es bedeutsam,
im Divisor (der Summe) ein Dollarzeichen zu setzen.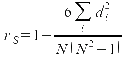 einsetzen:
einsetzen:
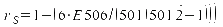 .
. erscheint die Regressionsgerade im Streudiagramm.
erscheint die Regressionsgerade im Streudiagramm.