Beispiele und Aufgaben im Modul Itemanalyse
Modul 3:
Itemanalyse mit SPSS
Arbeitsschritt:
Beispiele und Aufgaben
Da diese Prüfung
der Daten auf PC-gestützte Datenverarbeitungsprogramme (wie im
Folgenden auf SPSS) zurückgreift, empfiehlt es sich parallel
zur Bearbeitung dieses Moduls eine Einführung in SPSS und in
die deskriptive Statistik (etwa die Module von ViLeS 1) heranzuziehen.
Die einzelnen Analysekonzepte werden im Folgenden anhand einer
konkreten Fragestellung und des Analyseprogramms SPSS entwickelt.
Als Ausgangslage sei der
Datensatz zur Untersuchung der Frage gegeben, ob das Zeitmuster von
Studierenden von den Prinzipien der protestantischen Ethik nach M.
Weber geprägt ist (vgl. Hans-Günther Heiland, Werner
Schulte: Zeit und Studium. Untersuchungen zum Zeitbewusstsein und zur
Zeitverwendung von Studierenden. Centaurus-Verlag, Herbolzheim 2002).
Der Datensatz beruht auf der folgenden Itembatterie (Ausschnitt) zur
Entwicklung einer Skala zur protestantischen Ethik (im Folgenden
PE-Skala) :
Tabelle 3-16:
Itembatterie zur PE-Skala (Wiederholung)

Quelle :
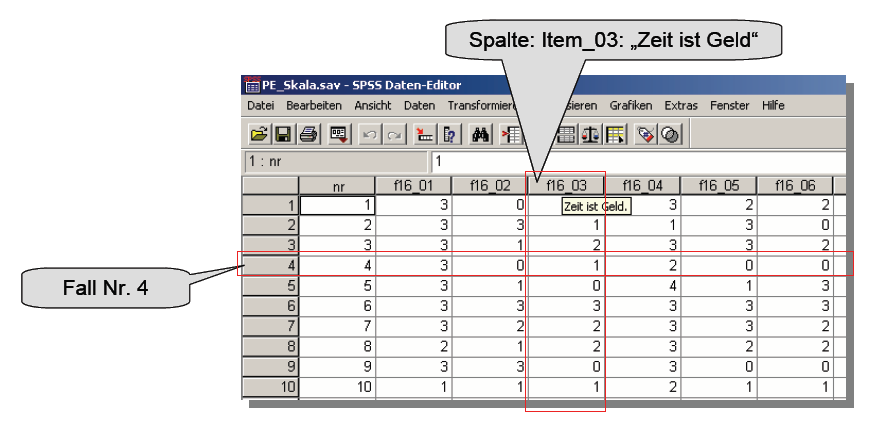
Die Daten sind als SPSS-Datei
gespeichert und werden im nachstehenden Datenfenster visualisiert:
Schaubild 3-4:
Datenmatrix PE-Skala - SPSS
A) Analyse der
Rohwertverteilung der Items
1. statistische
Parameter der eindimensionalen Häufigkeitsverteilung
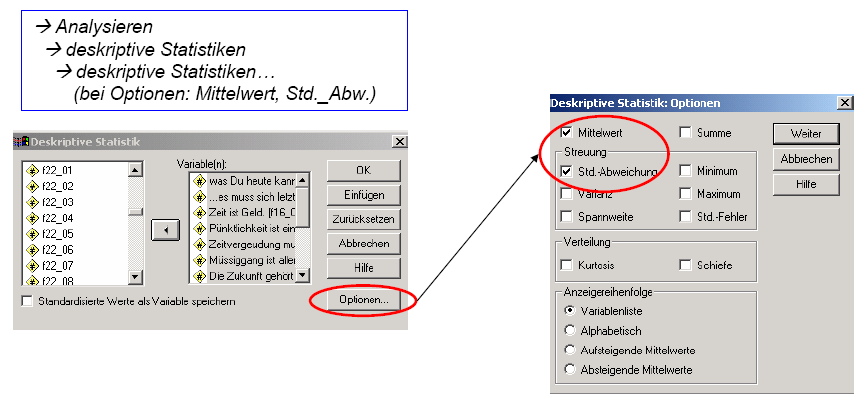
Zur Ermittlung der
deskriptive Statistiken (Mittelwerte, Standardabweichungen)
sind die folgenden SPSS - Befehle auszuführen:
Schaubild 3-5 :
SPSS – Befehle zur Verteilunganalyse
Über den darüber
erzielten SPSS – Output (dekriptive Statistik):
Tabelle 3-17: SPSS- Output
Deskriptive Statistik
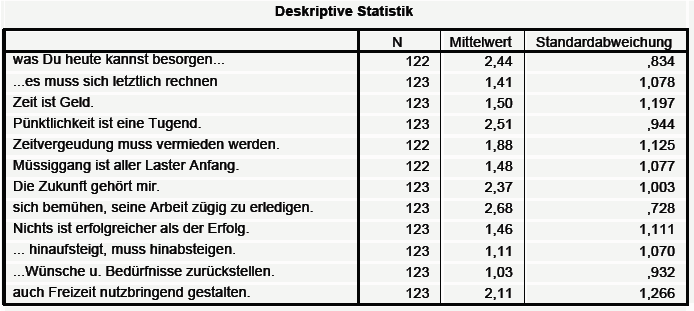
lassen sich die nachstehenden
Erkenntnisse formulieren:
(a) zum rechnerischen
Mittelwert:
Viele Items belegen den
unteren Skalenbereich bis zu 1,5 und liegen damit im Ablehnungsbereich.
5 Items sind eher im Zustimmungsbereich, d.h. >2. Kein
Mittelwert fällt in eine Randklasse.
(b) zur Standardabweichung:
Die Bedeutung der Streuung
für den diagnostischen Wert eines Items liegt in ihrer Aussage
über das Differenzierungsvermögen begründet.
Die meisten Items haben einen Wert >1 und sind damit eher
heterogen.
2. Graphische
Darstellung von Median und Quartilen im Boxplot
In Boxplots werden die Qartilsabstände
einer Verteilung graphisch dargestellt. Sie lassen sich über
folgende SPSS - Befehle erzeugen:
Schaubild 3-6: SPSS
– Eingabe zur Erzeugung von Boxplots:
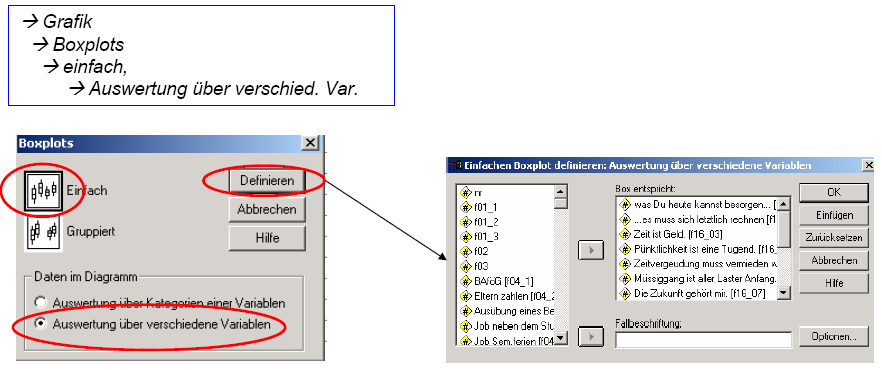
Abbildung 3-17:
SPSS – Output, Boxplots
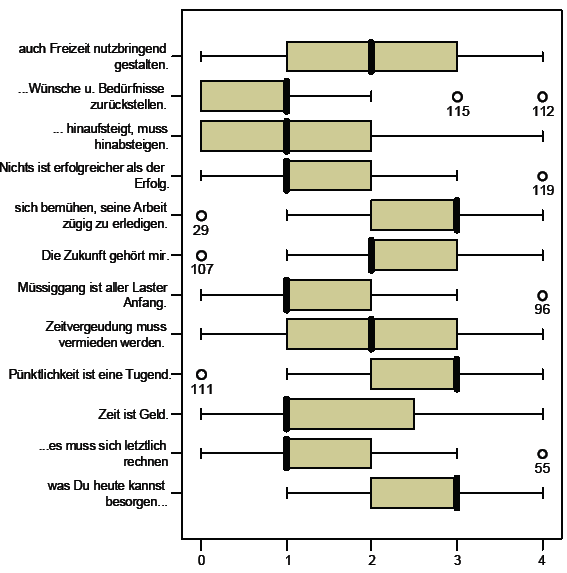
Bei einer geringen
Skalenbreite können, wie im Schaubild, auch Quartile
zusammenfallen. Die Quartilsabstände sind bis auf die der
zweiten Variablen (von oben) hinreichend groß genug und
liegen auch meist im mittleren Bereich , so dass die meisten Items in
Bezug auf die Einstellung PE eine ausreichende diskriminierende
Qualität aufweisen.
B)
Schwierigkeit einer Aufgabe (Item)
Eine Möglichkeit,
die akzeptablen Items zu identifizieren, ist die über die
Item-Mittelwerte. Wie die folgende Abbildung zeigt, liegen alle
Item-Mittelwerte im akzeptablen, 20% bis 80%-Bereich der Skala, d.h.
etwa zwischen den Skalenwerten 1 und 3.
Abbildung 3-18:
Itemanalyse: akzeptable Item - Mittelwerte
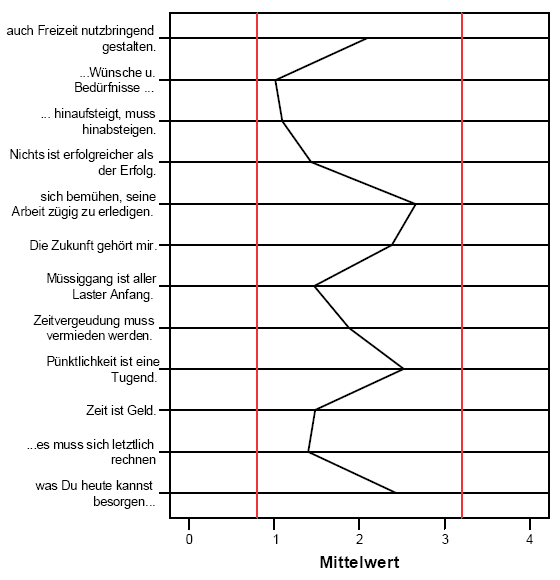
Diese Graphik
läßt sich wie folgt mit SPSS erstellen:
Schaubild 3-7: SPSS –
Eingabe zur Erzeugung von Item -Mittelwerten
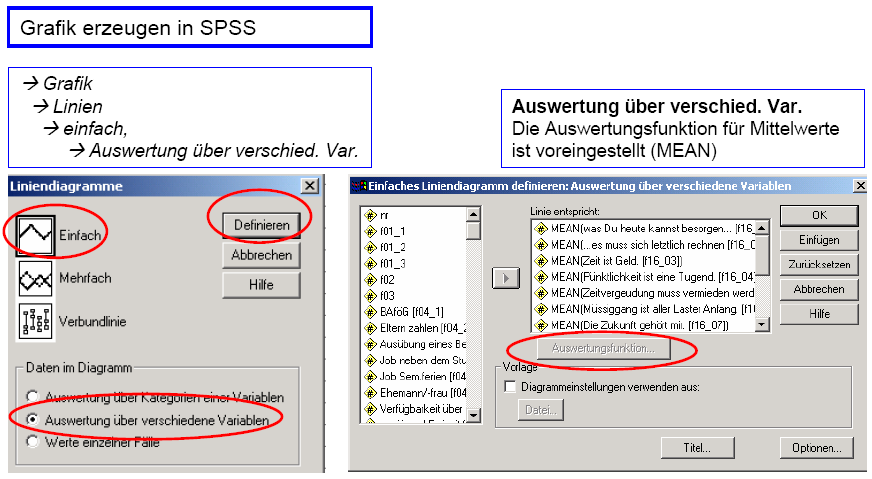
Schaubild
3-8: SPSS – Eingabe zur Erzeugung von Mittelwert-Graphiken
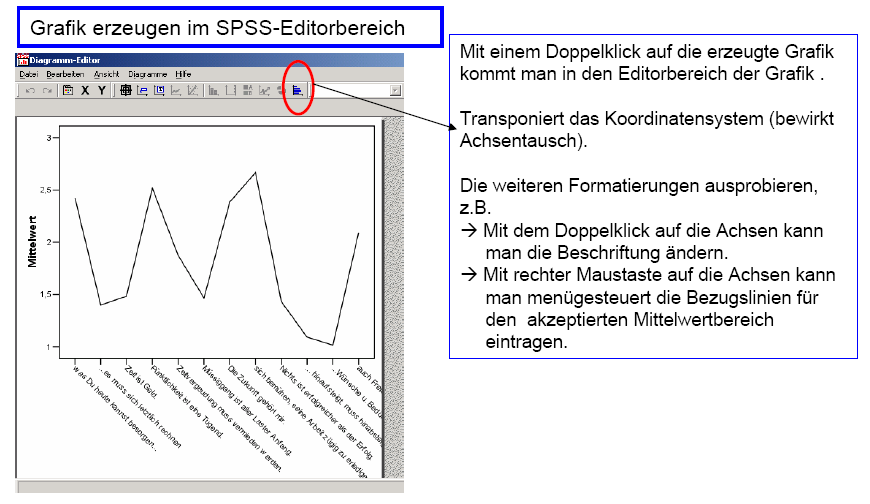
2.
Berechnung des Schwierigkeitsindexes
Der Schwierigkeits-Index war als
Anteil der von den n befragte Personen erreichten (beobachteten)
Itemwerte zu den gesamt erreichbaren Itemwerten definiert. Die Summe
der angekreuzten Item-Werte der Personen 1 bis 124 (Summenwerte der
Items) wird in Bezug zum insgesamt möglichen Punktwert der
Items gesetzt, wobei der maximal mögliche Punktwert (hier: 124
Befragte x 4 Ausprägungen) = 496 ist. Mit SPSS ist dieser Index
über mehrere Stufen zu ermitteln:
(a) Berechnung der
Itemsumme pro Person mit SPSS
Schaubild 3-9: Berechnung der Itemsumme
der Aufgaben je Person (Beispiel PE-Skala, Auszug)
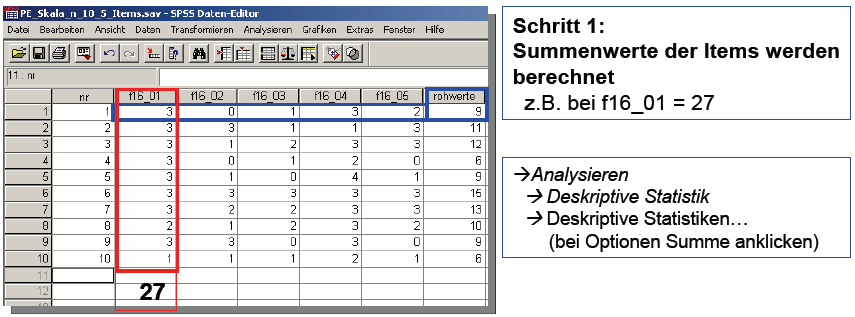
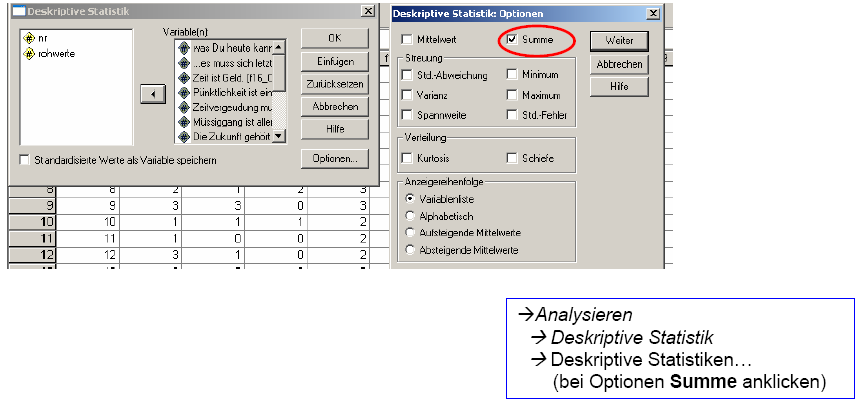
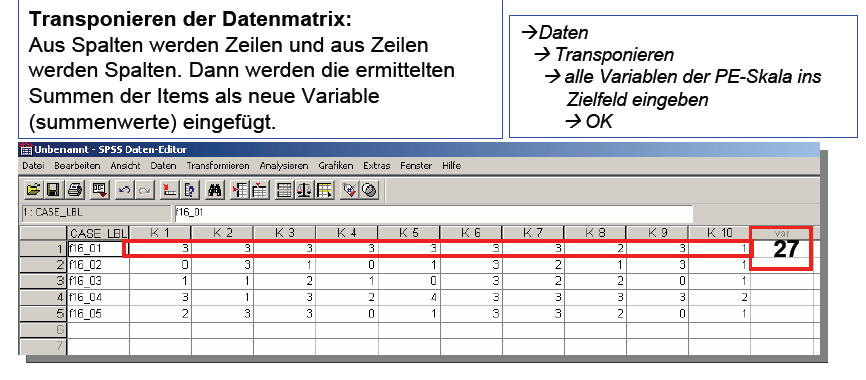
(b) Transponieren der
Datenmatrix und Eingabe der Summenwerte
Schaubild 3-10: SPSS
– Zur Eingabe von Item -Mittelwerten

(c) Ergebnis der
Transponierung
Schaubild
3-11: SPSS - Transponieren der Datenmatrix
(d)
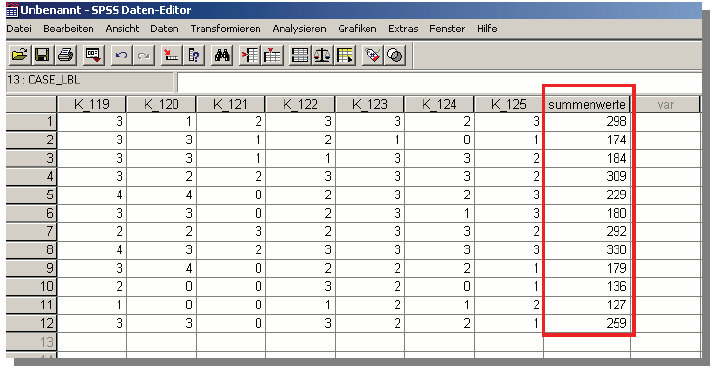
Einfügen der Summenwerte in die transponierte Datenmatrix
Schaubild 3-12: SPSS
– Zur Eingabe der Summenwerte
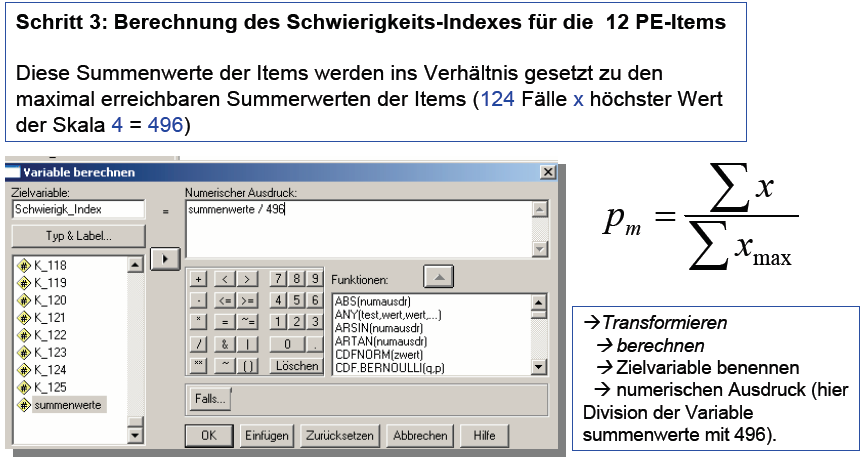
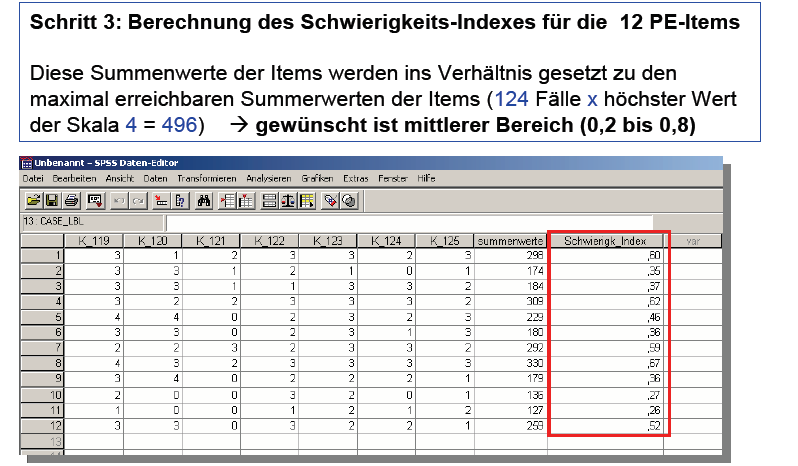
(e) Berechnung des
Schwierigkeitsindexes
Schaubild 3-13: SPSS
– Zur Berechnung des Schwierigkeitsindexes
C)
Trennschärfeanalyse
1. Berechnung der
Trennschärfe
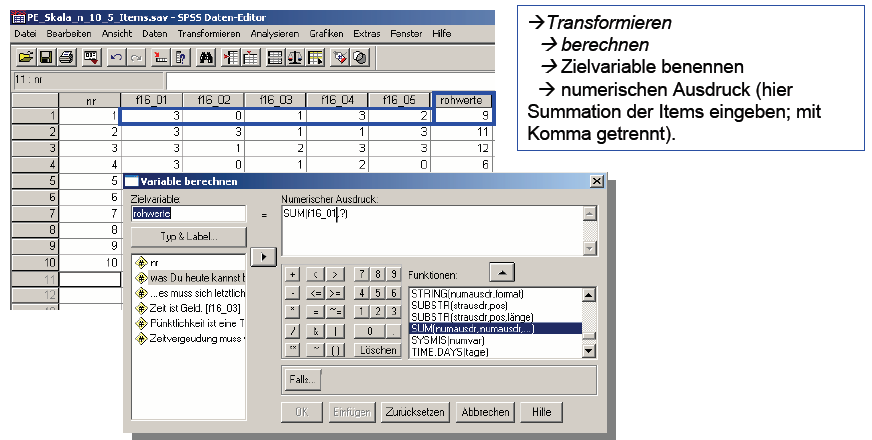
(a) Berechnung der Gesamttestwerte (Rohwerte)
Die Gesamtestwerte werden mit SPSS
als Item - Summe berechnet
(Beispiel PE-Skala, Auszug) und als neue Variable
„Rohwerte“ in die Datenmatrix aufgenommen.
Schaubild 3-14: SPSS - Abbildung
: Berechnung der Summe der erreichten Items
(b) Analyse der
Verteilung der Gesamttestwerte (Rohwerte)
Abbildung 3-19:
Verteilung der Gesamttestwerte
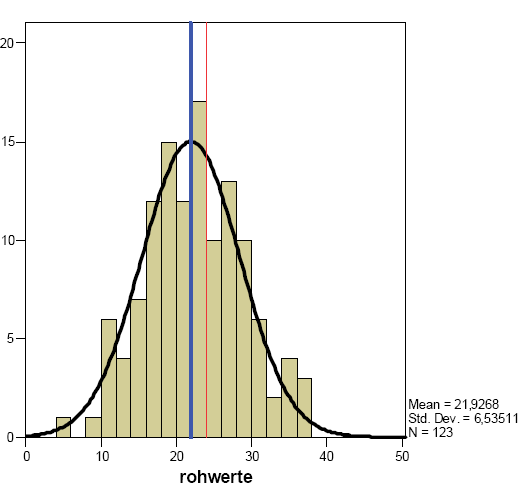
Anmerkung:
Blaue Line = arithmetisches Mittel der beobachteten Werte (MEAN)
Rote
Bezugslinie: theoretischer Mittelwert der Rohwerte (12 Items x 4 = 48/2
=24)
Die Standardabweichung, d.h.
die durchschnittliche Abweichungen der Werte vom Mittelwert liegt mit
+/-6,53511 im akzeptablen Bereich von 32% bis 59%,der Beobachtungen,
d.h. innerhalb der üblichen 20-80%-Grenze.
(c) Berechnung der
Korrelationskoeffizienten
Die
Korrelationskoeffizienten zwischen den einzelnen Items und dem
Gesamttest (Rohwerte) wird in den oberen Sreen-Shots, die
dazugehörende Befehlsyntax darunter dargestellt.
Schaubild 3-15: SPSS - Abbildung
: Berechnung der Korrelationskoeffizienten
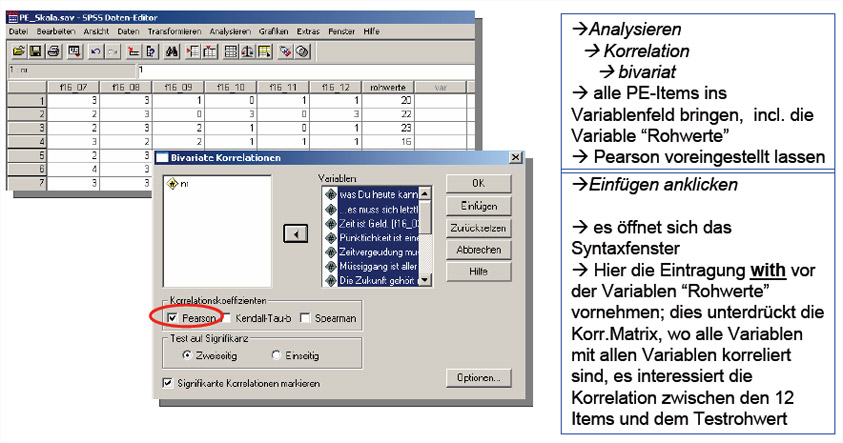
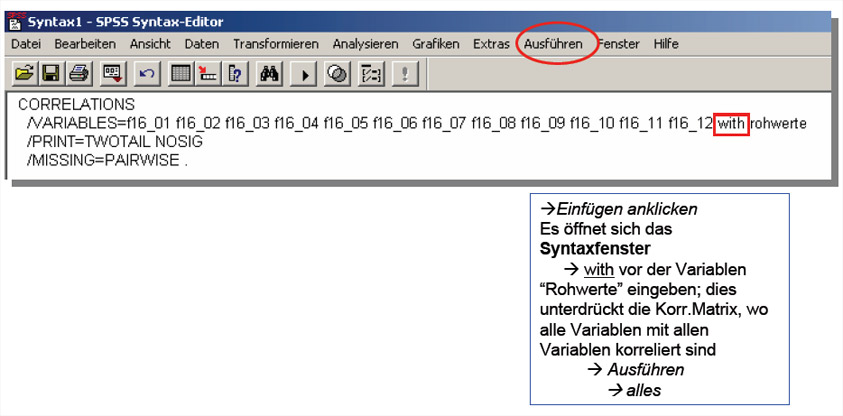
Schaubild 3-16: Syntax
der SPSS- Prozedur Korrelation
2. Analyse der
Trennschärfekoeffizienten
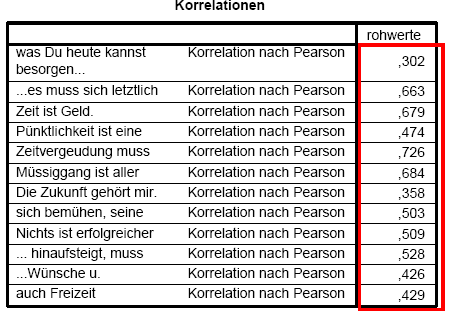
Die ermittelten
Korrelationskeffizienten werden – wie ausgeführt-
als Trennschärfekoeffizienten interpretiert. Sie
können Werte zwischen 0 und 1 annehmen. Items mit einem Trennschärfekoeffizienten < 0,2
können verworfen werden. In der nachfolgenden Tabelle ist kein
solches Item vorhanden, d.h. alle Items können verwendet
werden.
Tabelle 3-18: SPSS-Output
- Korrelationskoefizienten
D) Analyse des
Zusammenhangs zwischen Trennschärfekoeffizient und
Schwierigkeitsindex
Items mit geringer
Trennschärfe sollten zusätzlich nach ihrer
Schwierigkeit beurteilt werden. Im Rahmen dieser weiteren
Selektionsbemühungen werden die
Trennschärfekoeffizienten in die transponierte SPSS-Datei
eingetragen.
Schaubild 3-17: SPSS - Erweiterung
der transponierten Daten-Matrix
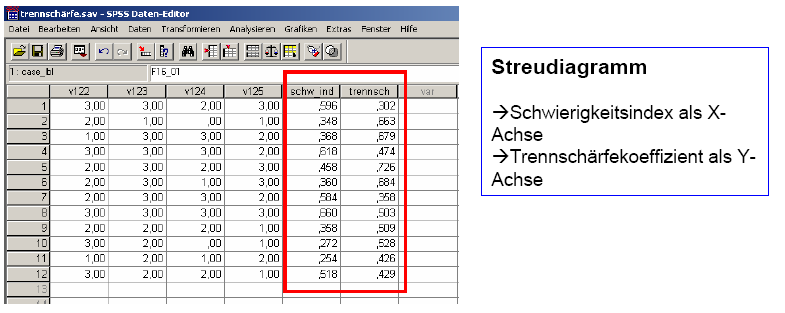
Die
Werte der beiden Variablen Trennschärfekoeffizient und
Schwierigkeitsindex werden dann in einem Streuungdiagramm dargestellt:
Schaubild 3-18: SPSS Befehle zur Erstellung
eines Streuungsdiagramms
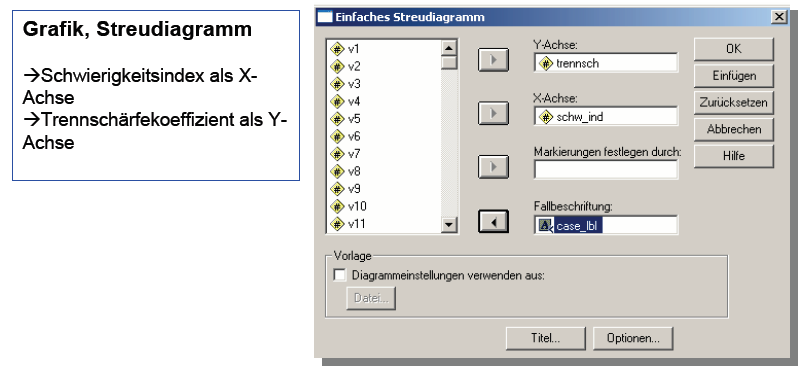
Abbildung
3-20: SPSS-Output - Streuungsdiagramm
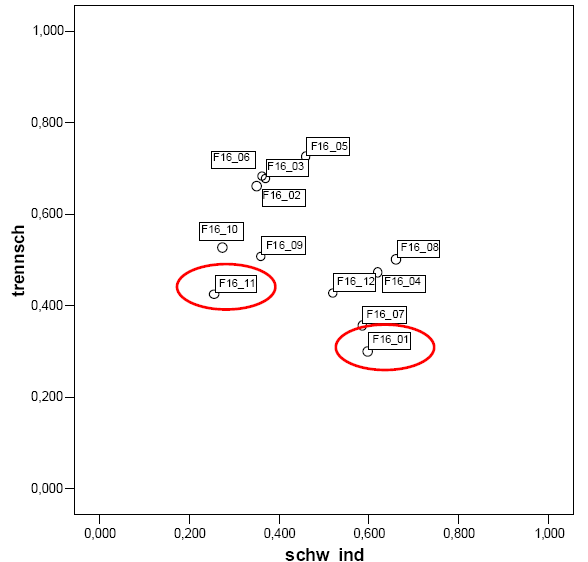
Ein etwas problematisches
Item ist F16_11 (“Man muss seine
Wünsche…”)
E)
Cronbach’s Alpha
Cronbach’s Alpha
basiert auf der Korrelationsmatrix der Items. Beispielsweise gibt es
bei den folgenden vier ausgewählten Items4 Items 4x(4-1)/2 = 6
Interkorrelationen:
Tabelle 3-19:
Interkorrelationsmatrix der Items

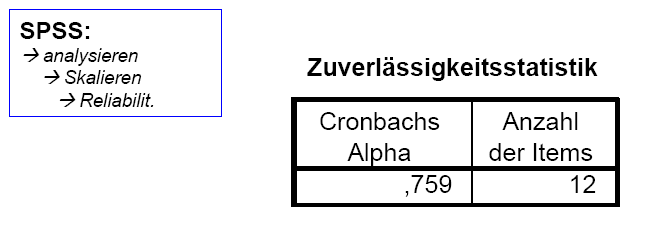
Für alle 12 Items
ließ sich über über die SPSS - Prozedur
„Reliabilität“ ein Alpha-Wert von 0,759
ermitteln, was auf eine zufriedenstellende bis gute Konsistenz der
verendeten Items hinweist.
Schaubild 3-19: SPSS
– Eingabe zur Berechnung von Cronbach’s Alpha
F) Skalenanalyse
Mit der Skalenanalyse wird
die Eindimensionalität bzw. Homogenität eines Items
geprüft. Es geht dabei um folgende Fragen:
-
Misst der Test ein einziges,
einheitliches Merkmal?
-
Kann ein- und derselbe
Testscore für verschiedene Personen Unterschiedliches
bedeuten?
-
Liegen die verschiedenen
Punkte des Messwertekontinuums auf einer einheitlichen Dimension?
Man muss also beispielsweise
begründen können, dass es für die Bedeutung
eines Testwerts unerheblich ist, durch welche Einzelleistungen er
zustande gekommen ist.
Die Berechnung eines
Gesamtwertes als Summe von Einzel-Items gilt dann als gerechtfertigt,
wenn empirisch nachgewiesen wird, dass alle Items
„dasselbe” messen.
|