Sollte das Drucken mit diesem Schaltknopf nicht funktionieren, nutzen Sie bitte die Druckfunktion in Ihrem Browser: Menü Datei -> Drucken

A) Der Messprozess

Wenn die im empirischen Forschungsprozess erhobenen qualitativen und quantitativen Informationen in einer größeren Anzahl anfallen, ist es sinnvoll diese Informationen elektronisch zu verarbeiten. Dies bedeutet, dass man in einem ersten Schritt, der Kodierung, auch verbalen und nonverbalen Erhebungskategorien numerische Werte zuweist. Dieses Vorgehen ist vor allem dann angebracht, wenn die Daten mit Hilfe von Computern erfasst werden soll, um die angefallenen Merkmalsausprägungen zu ordnen und statistisch auszuwerten.

Es hängt vom Ausmaß der Standardisierung des Erhebungsinstruments ab, ob die folgenden Überlegungen und die Entwicklung von Meßskalen Element des Operationalsierungsprozesses sind und damit vor der Erhebung anstehen oder erst nach der Erhebung durchgeführt werden können und damit Teil der Datenauswertung sind. In einem standardisierten Fragebogen mit geschlossenen Fragen sind die Skalen mit den zulässigen Antworten bereits vorzugeben. Die Gültigkeit und Zuverlässigkeit der Messung ist dann nach der Erhebung zu prüfen (vgl. Itemanalyse). Bei einem sehr offenen Erhebungsansatz können die Skalen erst auf der Basis der eingegangenen Ergebnisse konstruiert werden.

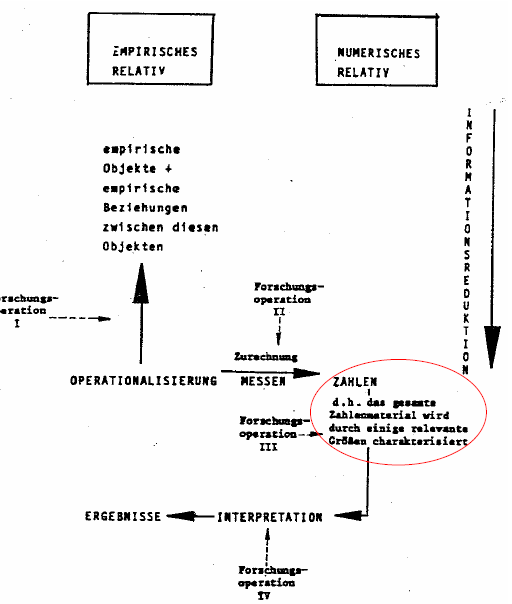
Der oa Zuordnungsprozess wird als Messen bezeichnet. Er ist strengen formalen Regeln zu unterwerfen. Wichtig ist dabei, dass die Zahlen weder doppelt vergeben noch inhaltlich verschiedenen Ausprägungen gleiche Zahlen zugeordnet werden. Man nennt dies eine eineindeutige Beziehung zwischen Merkmalsausprägung und Zahlenwert.

Die Messtheorie definiert: „Messen ist eine Zuordnung von Zahlen zu Objekten oder Ereignissen, sofern diese Zuordnung eine homomorphe Abbildung eines empirischen Relativ in ein numerisches Relativ ist“ (Bortz: /Döring 1995: 65).

Dafür sind folgende Aspekte relevant:

1. Es erfolgt eine Zuordnung von Zahlen zu Merkmalen von Objekten (Merkmalsträgern).

2. Dabei sollen die Relationen der Merkmalsträger bezüglich des Merkmals bzw. der Merkmalsausprägung durch die ihnen zugeordneten Zahlen wiedergegeben werden.

3. Somit ist der Meßvorgang die Konstruktion eines numerischen Relativs zu einem gegebenen empirischen Relativ.

Was heißt das?

Ein empirisches Relativ besteht aus einer Menge von N Objekten zwischen denen eine oder mehrere Beziehungen bestehen (Relationssystem).

Ein numerisches Relativ ist eine Ordnung von Zahlen, die ebenfalls zueinander in Beziehung stehen.

Die Zuordnung des numerischen zum empirische relativ ist homomorph (strukturgleich), d.h. die Beziehung der empirischen Objekte müssen in der numerischen Struktur so abgebildet sein, dass die Eigenschaften der empirischen in den numerischen Beziehungen erhalten bleiben.

Abbildung 3-1: Konzeptionelle Grundlagen der Meßtheorie

B) Die Konstruktion von Skalen

Die Regeln, mit denen die verschiedenen Ausprägungen und Charakteristika der Beobachtungen in numerische Werte transformiert werden, werden in einer Skala festgelegt. „Unter einer Skala versteht man ein empirisches Relativ, ein numerisches Relativ und eine die beiden Relative verknüpfende, homomorphe Abbildungsfunktion. Die Messbarkeit eines Merkmals bzw. die Konstruierbarkeit einer Skala ist an Bedingungen geknüpft“ (Bortz/Döring 1995: 65).

Die Skalierung eines Sachverhalts erfordert nach Strübing (TU Berlin) die Klärung der folgenden 3 Fragen:

• Gelten die Beziehungsregeln der Skala auch im empirischen Relativ?

• Gibt es eine passende Abbildungsregel und ein numerisches Relativ (Repräsentationsproblem)?

• Welche Operationen sind erlaubt, ohne die Abbildungstreue zu gefährden (Eindeutigkeitsproblem)?

Auf der numerischen Ebene sind zwar alle Informationen formal gleich zu behandeln, nicht jedoch auf der inhaltlichen. So ist es sicher zulässig, die Einkommen verschiedener Haushaltsmitglieder zu einem Haushaltseinkommen zusammen zu fassen und eventuell ein durchschnittliches Einkommen zu errechnen. Unzulässig und auch unsinnig wäre es, die numerisch kodierten Familienstände (vgl. nachstehendes Beispiel) auf zu addieren und zu mitteln. Eine Lösung der oben angesprochenen 3 Probleme ist nur mittels unterschiedlicher Typen von Skalen möglich, die sich hinsichtlich ihrer formalen Qualität unterscheiden. Das Skalenniveau bezieht sich auf die hinter den Variablenwerten liegende zulässige Metrik und berührt auf grundsätzliche Weise die Rechenbarkeit der Zahlenwerte.

1. Nicht-metrischen Skalen

1. Nominalskalen„... bestehen lediglich aus einem Satz rangmäßig ungeordneter Kategorien..." (Benninghaus1982:22). In einer Nominal-Skala werden den Ausprägungen beliebige, aber eindeutige Zahlen zugeordnet. Dieser Vorgang impliziert keine Wertung oder die Festlegung einer Rangordnung, sondern nur eine Zuweisung. So kann z.B. das Geschlecht auf einer Nominal-Skala erfasst werden, in dem man die Ausprägung "weiblich" der 1 und "männlich" der 2 zuordnet.

2. Skalen, bei denen die Objekte/Werte nicht nur separat klassifiziert (wie in Nominalskalen), sondern die Kategorien auch rangmäßig geordnet werden können, heißen Ordinal-Skalen. Mit ihnen werden den Daten Ränge oder Wertigkeiten zugewiesen. So entsteht eine Ordnung, die aussagt, dass etwas größer oder kleiner, besser oder schlechte, akzeptabler oder weniger akzeptabel als etwas anderes ist. Wichtig ist, dass mit der Zuweisung von Ziffern keine Beschreibung über den Abstand der Ausprägungen erfolgt . So kann nicht gesagt werden, dass die Schulnote "gut(2)" doppelt so gut ist wie eine "ausreichend(4)". Ebenso wenig gibt eine Differenz von Ranglistenplätzen Auskunft über den Punkteabstand.

2. Metrische Skalen

1. Mit einer Intervall-Skala lassen sich fest stehende Differenzen ausdrücken. So beträgt die Differenz zwischen 5°C und 10°C genau 5°C und damit eben soviel wie zwischen 20° und 25°. Eine Ordinal-Skala könnte nur ausweisen, dass 20°C wärmer als 15°C ist. Die Differenzen lassen sich also quantifizieren, nicht aber die Verhältnisse, weil diese Skala keinen absoluten Nullpunkt aufweist.

2. Die Verhältnis-Skala ist eine Erweiterung der Intervall-Skala. Ihr Werte beziehen sich auf einen natürlichen Nullpunkt! Damit verhalten sich die Zahlenwerte auch proportional zueinander.

3. Bei der Absolut-Skala gibt es zusätzlich ein natürliches Zählintervall. Bei einer Verkehrszählung können nur "ganze" Autos gezählt werden. Eine Verhältnis-Skala der Länge oder des Einkommens kann im Gegensatz zur Absolut-Skala in vielen weiteren Maßeinheiten (Längenmaßen, Währungseinheiten) ausgedrückt werden.

In der Praxis wird meist nur zwischen drei Skalenarten unterschieden: der Nominal-, der Ordinal- und den metrischen Skalen. Für die Datenerfassung und Berechnung macht es keinen Unterschied, ob es sich bei den metrischen Skalen um eine Intervall-, Verhältnis- oder Absolutskala handelt.

3. Schemata zum Skalenniveau

Die verschiedenen Kriterien zur Bestimmung des Skalenniveaus sind in den folgenden Schemata zusammen gefasst:

Tabelle 3-1: Skalenniveaus, Begriffsübersicht

Tabelle 3-2: Skalenniveaus, Aussagen und Beispiele

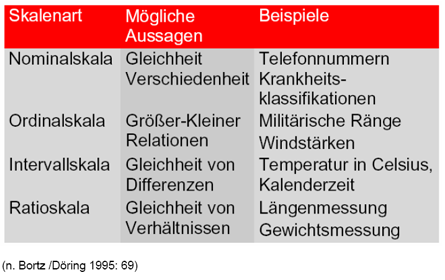
Tabelle 3-3: Skalenniveaus, metrische Eigenschaften

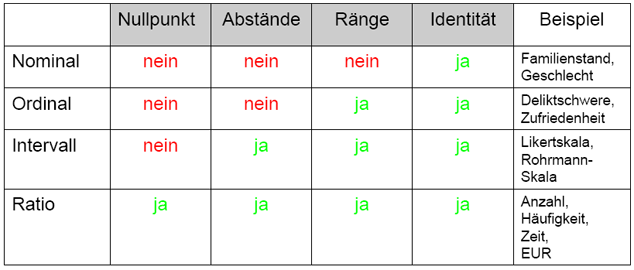
Da viele statistischen Auswertungen mit Summen oder Produkten von Merkmalswerten operieren, bestimmt das Skalenniveau in beträchtlichem Maße die Verwendbarkeit statistischer Analysemodelle. Genaueres dazu findet sich in den entsprechenden statistischen Modulen der Plattform.

Tabelle 3-4: Skalenniveaus, formale Relationen und statistische Zulässigkeit

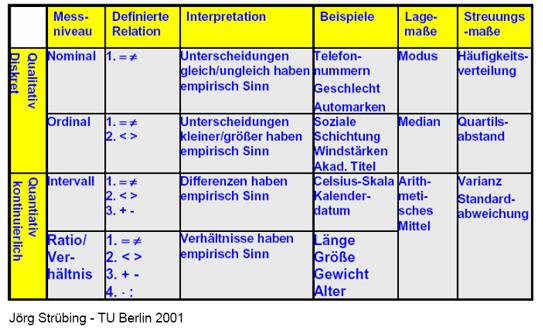
Weil jede Skala die Eigenschaften der jeweils niedrigeren mit enthält, kann sie auf ein niedrigeres Skalenniveau transformiert werden (z.B. von Verhältnis- auf Ordinal- oder Nominalskalenniveau). Derartige Transformationen, die zwangsläufig mit einem Informationsverlust verbunden sind, werden in der Regel durchgeführt, wenn eine Variable höheren Skalenniveaus mit einer anderen niedrigeren Niveaus in Verbindung gebracht werden soll oder eine übersichtlichere Darstellung angestrebt wird.

Abbildung 3-2: Skalenniveaus, kumulative Hierarchie

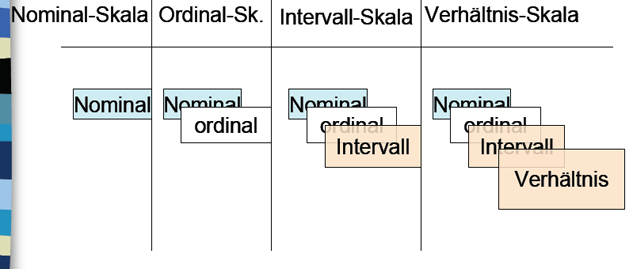
Die wichtigsten Differenzierungskriterien sind nochmals in diesem Link (Schema) zusammengefasst.

C) Diskrete und stetige Merkmale

Aus Daten metrischen Skalenniveaus resultieren zwei Arten von Variablen: diskrete und stetige. Im Folgenden sollen die beiden Merkmale der Variablenarten kurz aufgezeigt werden. Diskrete Variablen nehmen nur begrenzte oder abzählbare Werte an, in vielen praktischen fällen sogar nur ganze Zahlen, z.B. die Größe einer Personengruppe oder der Preis einer Ware in Cent. Stetige (auch kontinuierliche) Variablen können jeden Zahlenwert annehmen und sind nicht zählbar, so vor allem Längen- und Gewichtsmaße.

Die Eigenschaft stetig/diskret ist in der empirischen Forschung eng mit dem Problem der Messgenauigkeit verknüpft. So ist das Merkmal Temperatur in der Natur stetig. Die als Ergebnis von Messvorgängen resultierenden Werte der Variablen Temperatur sind jedoch, bedingt durch die Messgenauigkeit des Thermometers, de facto diskret. Deshalb gilt es, die inhaltliche Interpretation von Wertdifferenzen unterhalb der Messgenauigkeit zu vermeiden. Dies wird im Rahmen empirischer Erhebungen leicht übersehen, wenn etwa nach den ungefähren Monatsausgaben für bestimmte Produktgruppen gefragt wird (was naturgemäß stark gerundete Werte ergibt), diese jedoch mit höchster Rechengenauigkeit ausgewertet und geringe Differenzen zwischen verschiedenen Vergleichsgruppen inhaltlich interpretiert werden. Noch deutlicher tritt dieses Problem bei Untersuchungen zu Tage, bei denen die Messgenauigkeit der Erhebungsinstrumente nur schwer zu ermitteln ist, beispielsweise bei der Erhebung von Meinungen und Einstellungen (vgl. dazu auch die Stichworte Zuverlässigkeit und Gültigkeit).

letzte Änderung am 5.4.2019 um 4:24 Uhr.

Adresse dieser Seite (evtl. in mehrere Zeilen zerteilt)
http://viles.uni-oldenburg.de/navtest/viles0/kapitel03_Datenmessung~~lund~~l-aufbereitung/modul01_Messen~~lund~~lSkalieren/ebene01_Konzepte~~lund~~lDefinitionen
/03__01__01__01.php3